人教版四年级数学下册 5-2三角形的分类 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版四年级数学下册 5-2三角形的分类 同步拓展讲与练+奥数培优(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 713.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 16:57:42 | ||
图片预览


文档简介
三角形的分类
知识引入:
一、三角形的特征
例题1:填空。
(1)三角形按角分可分为( )三角形、( )三角形和( )三角形。
(2)直角三角形有( )个锐角,钝角三角形有( )个锐角,锐角三角形有( )个锐角。
(3)一个三角形中最多有( )个钝角,最少有( )个锐角。
(4)有一个三角形,最大的角是89度,这是一个( )三角形。
(5)两条边( )的三角形叫做等腰三角形,其中相等的两条边叫做( ),另一条边叫做( ),底边上的两个角叫做( ),两腰的夹角叫做( )。
(6)两个锐角相等的直角三角形,同时也是( )三角形。
例题2:选一选。
(1)等边三角形中有( )个角相等。
A.1 B.2 C.3 D.无法确定
(2)三条边的长度都是5厘米的三角形是( )。
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
(3)一个直角三角形的( )最长。
A.直角边 B.斜边 C.高 D.无法确定
(4)等腰三角形一定是( )三角形。
A.锐角 B.钝角 C.直角 D.无法确定
知识精讲:三角形的分类
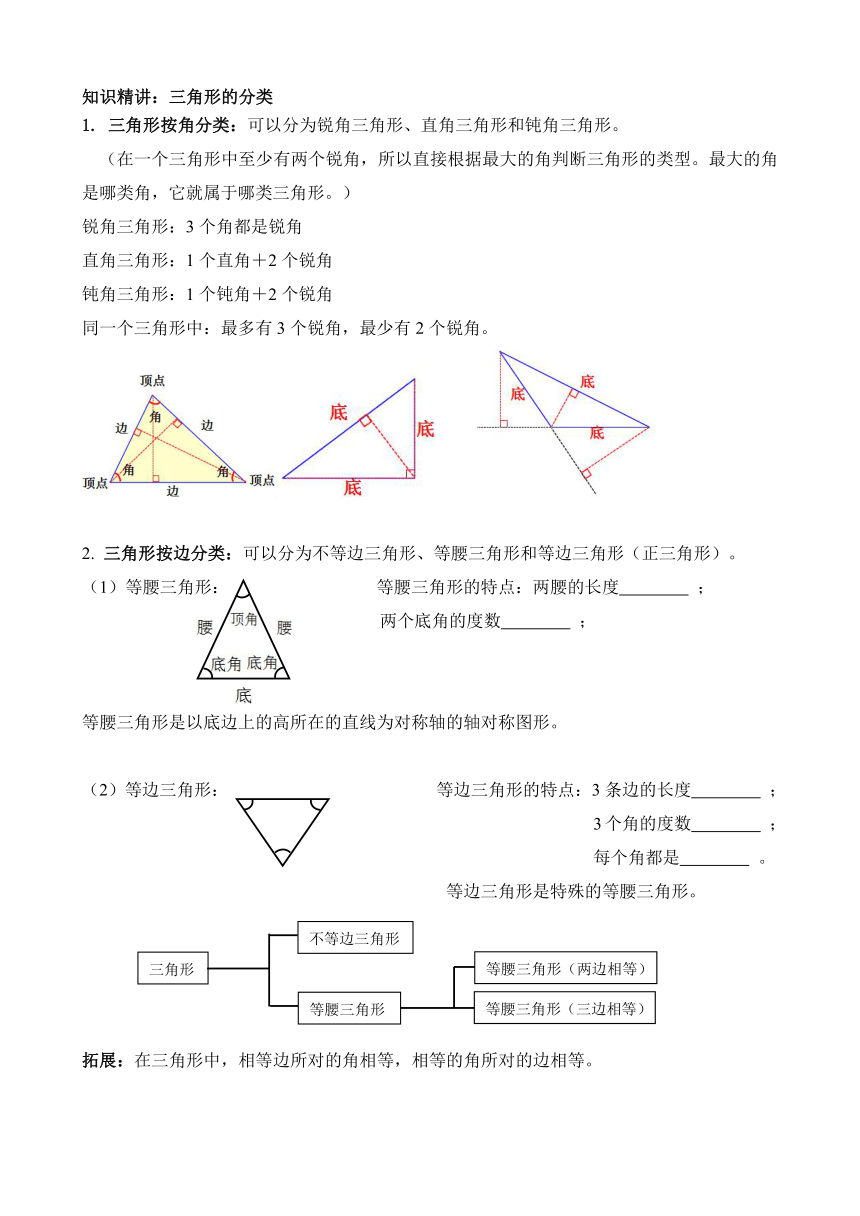
1. 三角形按角分类:可以分为锐角三角形、直角三角形和钝角三角形。
(在一个三角形中至少有两个锐角,所以直接根据最大的角判断三角形的类型。最大的角是哪类角,它就属于哪类三角形。)
锐角三角形:3个角都是锐角
直角三角形:1个直角+2个锐角
钝角三角形:1个钝角+2个锐角
同一个三角形中:最多有3个锐角,最少有2个锐角。
三角形按边分类:可以分为不等边三角形、等腰三角形和等边三角形(正三角形)。
(1)等腰三角形: 等腰三角形的特点:两腰的长度 ;
两个底角的度数 ;
等腰三角形是以底边上的高所在的直线为对称轴的轴对称图形。
(2)等边三角形: 等边三角形的特点:3条边的长度 ;
3个角的度数 ;
每个角都是 。
等边三角形是特殊的等腰三角形。
拓展:在三角形中,相等边所对的角相等,相等的角所对的边相等。
巩固练习:
1.填空。
(1)三角形有( )条边,( )个顶点,( )个角。
(2)三角形按角可以分为( )三角形、( )三角形和( )三角形。
(3)三条边相等的三角形叫做( )三角形,又叫做( )三角形。
(4)等腰三角形的两个底角( )。
(5)两个完全相同的等腰直角三角形一定能拼成一个( )形。
(6)三角形按角分类可以分为( )三角形、( )三角形和( )三角形。
(7)一个三角形中,最多有( )个锐角,最少有( )个锐角,最多有( )个直角。
(8)两条边( )的三角形叫作等腰三角形。
(9)三条边( )的三角形叫作等边三角形,又叫作( ),三个角都是( )°。
(10)一个直角三角形,其中的一个锐角是45°,它也是( )三角形。
(11)锐角三角形有( )个锐角。
(12)在钝角三角形中,钝角所对的边( )。(最短 最长 不确定)
(13)一个直角三角形的一个锐角是50°,则另一个锐角是( )。
(14)如果一个三角形有两个内角的度数之和等于90°,这个三角形一定是( )三角形。
(15)一个等腰三角形中,顶角为80°,它的底角均为( )。
2.我是小法官,对错我来判。
(1)一个三角形中,如果有两个锐角,必定是一个锐角三角形。 ( )
(2)所有的等腰三角形一定是锐角三角形。 ( )
(3)所有的等边三角形都是等腰三角形。 ( )
(4)一个三角形中最多有两个直角。 ( )
(5)把一个大三角形平均分成两个大小相等的小三角形,每个小三角形的内角和是90°。 ( )
(6)锐角三角形的内角和小于钝角三角形的内角和。 ( )
(7)一个等腰三角形,当一个底角大于45°时,这个等腰三角形一定是锐角三角形。 ( )
(8)一个角是60°的等腰三角形不一定是等边三角形。 ( )
(9)三角形任意两个内角之和大于第三个内角。 ( )
(10)一个钝角三角形的两个内角之和一定小于90°。 ( )
3.把下面三角形的序号填在相应的圈里。
4.说出下面每个三角形的名称,并画出底边上的高。
5.动笔画一画。画一个直角边是3厘米的等腰直角三角形。
6.解决问题。
(1)有一块菜园,它的外面用篱笆围成了一个等边三角形,其中一条边长15米,这个篱笆的周长是多少米?
(2)请你用纸剪一个等边三角形,并画出它的三条高,再沿着高折一折,把你的发现写下来。
(3)右图中有( )个锐角三角形,( )个钝角三角形,( )个直角三角形。
(4)王大爷家有一个等腰三角形形状的靠墙的鸡圈,已知这个等腰三角形的腰长为56分米,底长为35分米,制作这个鸡圈最多需要多长的篱笆?
(5)把一个边长为6厘米的正三角形,改装成一个等腰三角形,这个等腰三角形的底和腰可能各是多少厘米?(要求改装后的等腰三角形的每条边长都是整理米数。)
(6)在下面的点子图上分别画一个锐角三角形,一个直角三角形和一个钝角三角形。
奥数思维拓展:运用尝试法解决图形分割问题
1.渗透一种数学思想:模型思想
2.学习两类思维方法:实践操作法法、尝试法
思维提升
[例]你能把一个直角三角形分割成一个锐角三角形和一个钝角三角形吗?
[分析与解答]
(1)尝试从直角三角形的两个锐角顶点向它们的对边任意一点连线,这样总会得到一个直角三角形和一个钝角三角形,这样分割是不符合题意的。
(2)再尝试从三角形的直角顶点向它对边的任意一点连线(注意不能与斜边上的高重合),这样分割就会得到一个锐角三角形和一个钝角三角形。
[技巧]
在尝试过程中,不断否定错误的思路,有助于掌握科学的学习方法。
[举一反三]
1.在下面的长方形中画一条线,把它分割成两个完全相同的直角三角形。
2.在下面的平行四边形中画一条线,把它分割成两个钝角三角形。
3.下面是一个钝角三角形,请你在图中画一条线,将其分割成两个三角形,一个是等腰三角形,另一个是直角三角形。
三角形
不等边三角形
等腰三角形
等腰三角形(三边相等)
等腰三角形(两边相等)
知识引入:
一、三角形的特征
例题1:填空。
(1)三角形按角分可分为( )三角形、( )三角形和( )三角形。
(2)直角三角形有( )个锐角,钝角三角形有( )个锐角,锐角三角形有( )个锐角。
(3)一个三角形中最多有( )个钝角,最少有( )个锐角。
(4)有一个三角形,最大的角是89度,这是一个( )三角形。
(5)两条边( )的三角形叫做等腰三角形,其中相等的两条边叫做( ),另一条边叫做( ),底边上的两个角叫做( ),两腰的夹角叫做( )。
(6)两个锐角相等的直角三角形,同时也是( )三角形。
例题2:选一选。
(1)等边三角形中有( )个角相等。
A.1 B.2 C.3 D.无法确定
(2)三条边的长度都是5厘米的三角形是( )。
A.锐角三角形 B.直角三角形
C.钝角三角形 D.无法确定
(3)一个直角三角形的( )最长。
A.直角边 B.斜边 C.高 D.无法确定
(4)等腰三角形一定是( )三角形。
A.锐角 B.钝角 C.直角 D.无法确定
知识精讲:三角形的分类
1. 三角形按角分类:可以分为锐角三角形、直角三角形和钝角三角形。
(在一个三角形中至少有两个锐角,所以直接根据最大的角判断三角形的类型。最大的角是哪类角,它就属于哪类三角形。)
锐角三角形:3个角都是锐角
直角三角形:1个直角+2个锐角
钝角三角形:1个钝角+2个锐角
同一个三角形中:最多有3个锐角,最少有2个锐角。
三角形按边分类:可以分为不等边三角形、等腰三角形和等边三角形(正三角形)。
(1)等腰三角形: 等腰三角形的特点:两腰的长度 ;
两个底角的度数 ;
等腰三角形是以底边上的高所在的直线为对称轴的轴对称图形。
(2)等边三角形: 等边三角形的特点:3条边的长度 ;
3个角的度数 ;
每个角都是 。
等边三角形是特殊的等腰三角形。
拓展:在三角形中,相等边所对的角相等,相等的角所对的边相等。
巩固练习:
1.填空。
(1)三角形有( )条边,( )个顶点,( )个角。
(2)三角形按角可以分为( )三角形、( )三角形和( )三角形。
(3)三条边相等的三角形叫做( )三角形,又叫做( )三角形。
(4)等腰三角形的两个底角( )。
(5)两个完全相同的等腰直角三角形一定能拼成一个( )形。
(6)三角形按角分类可以分为( )三角形、( )三角形和( )三角形。
(7)一个三角形中,最多有( )个锐角,最少有( )个锐角,最多有( )个直角。
(8)两条边( )的三角形叫作等腰三角形。
(9)三条边( )的三角形叫作等边三角形,又叫作( ),三个角都是( )°。
(10)一个直角三角形,其中的一个锐角是45°,它也是( )三角形。
(11)锐角三角形有( )个锐角。
(12)在钝角三角形中,钝角所对的边( )。(最短 最长 不确定)
(13)一个直角三角形的一个锐角是50°,则另一个锐角是( )。
(14)如果一个三角形有两个内角的度数之和等于90°,这个三角形一定是( )三角形。
(15)一个等腰三角形中,顶角为80°,它的底角均为( )。
2.我是小法官,对错我来判。
(1)一个三角形中,如果有两个锐角,必定是一个锐角三角形。 ( )
(2)所有的等腰三角形一定是锐角三角形。 ( )
(3)所有的等边三角形都是等腰三角形。 ( )
(4)一个三角形中最多有两个直角。 ( )
(5)把一个大三角形平均分成两个大小相等的小三角形,每个小三角形的内角和是90°。 ( )
(6)锐角三角形的内角和小于钝角三角形的内角和。 ( )
(7)一个等腰三角形,当一个底角大于45°时,这个等腰三角形一定是锐角三角形。 ( )
(8)一个角是60°的等腰三角形不一定是等边三角形。 ( )
(9)三角形任意两个内角之和大于第三个内角。 ( )
(10)一个钝角三角形的两个内角之和一定小于90°。 ( )
3.把下面三角形的序号填在相应的圈里。
4.说出下面每个三角形的名称,并画出底边上的高。
5.动笔画一画。画一个直角边是3厘米的等腰直角三角形。
6.解决问题。
(1)有一块菜园,它的外面用篱笆围成了一个等边三角形,其中一条边长15米,这个篱笆的周长是多少米?
(2)请你用纸剪一个等边三角形,并画出它的三条高,再沿着高折一折,把你的发现写下来。
(3)右图中有( )个锐角三角形,( )个钝角三角形,( )个直角三角形。
(4)王大爷家有一个等腰三角形形状的靠墙的鸡圈,已知这个等腰三角形的腰长为56分米,底长为35分米,制作这个鸡圈最多需要多长的篱笆?
(5)把一个边长为6厘米的正三角形,改装成一个等腰三角形,这个等腰三角形的底和腰可能各是多少厘米?(要求改装后的等腰三角形的每条边长都是整理米数。)
(6)在下面的点子图上分别画一个锐角三角形,一个直角三角形和一个钝角三角形。
奥数思维拓展:运用尝试法解决图形分割问题
1.渗透一种数学思想:模型思想
2.学习两类思维方法:实践操作法法、尝试法
思维提升
[例]你能把一个直角三角形分割成一个锐角三角形和一个钝角三角形吗?
[分析与解答]
(1)尝试从直角三角形的两个锐角顶点向它们的对边任意一点连线,这样总会得到一个直角三角形和一个钝角三角形,这样分割是不符合题意的。
(2)再尝试从三角形的直角顶点向它对边的任意一点连线(注意不能与斜边上的高重合),这样分割就会得到一个锐角三角形和一个钝角三角形。
[技巧]
在尝试过程中,不断否定错误的思路,有助于掌握科学的学习方法。
[举一反三]
1.在下面的长方形中画一条线,把它分割成两个完全相同的直角三角形。
2.在下面的平行四边形中画一条线,把它分割成两个钝角三角形。
3.下面是一个钝角三角形,请你在图中画一条线,将其分割成两个三角形,一个是等腰三角形,另一个是直角三角形。
三角形
不等边三角形
等腰三角形
等腰三角形(三边相等)
等腰三角形(两边相等)
