人教版四年级数学下册 5-3三角形的内角和 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版四年级数学下册 5-3三角形的内角和 同步拓展讲与练+奥数培优(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 186.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 16:58:19 | ||
图片预览



文档简介
三角形的内角和
知识引入:
三角形的内角和
例题1:填空。
(1)三角形的内角和是( )。
(2)把三角形三个角剪下来,顶点重合拼在一起可以拼成一个( )角。
(3)在能组成三角形的三个角后面的括号内画“△”,不能组成三角形的画“○”。
90° 42° 58°( )
40° 45° 70°( )
80° 80° 20°( )
125° 35° 20°( )
(4)长方形和正方形的四个角都是( )角,所以长方形和正方形的内角和都是( )。
(5)将任意一个四边形的四个角剪下来,可以拼成一个( )角,所以四边形的内角和是( )。
(6)可以将任意一个四边形分成( )个三角形,四边形的内角和是180°×( )=( )°。
例题2:算一算,判一判。
(1)∠1=50°,∠2=35°,∠3=( ),
这是一个( )三角形。
(2)∠1=42°,∠2=48°,∠3=( ),
这是一个( )三角形。
(3) ∠1=70°,∠2=55°,∠3=( ),
这是一个( )三角形,也是一个( )三角形。
(4)如下图,∠1是直角,∠2=33°,∠3=( )。
(5)等边三角形每个内角都是( )。
例题3:判断。
(1)一个三角形的内角和是180°,用两个完全一样的三角形拼成一个大三角形,这个大三角形的内角和为360°。( )
(2)三角形越大,它的内角和越大。( )
(3)有一个三角形的两个内角分别是91°和89°。( )
例题4:我会算 。
例题5:解决问题我能行 。
(1)四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?
(2)在四边形ABCD中,∠A=∠C=90°,∠ABE=∠CBE,∠ADF=∠CDF,则∠ABE+∠FDC等于多少度?
知识精讲:三角形的内角和
1.三角形的内角和:180°
拓展:三角形的一个外角等于它不相邻两个内角的和。
如图:∠4=∠1 + ∠2
三角形内角和的应用:
在三角形中,已知两个角的度数,求第三个角的度数,用内角和180°连续减去已知连个角的度数或减去这两个角的度数和。
3.多边形的内角和
(1)四边形的内角和是360°。
(2)多边形的内角和=180°×(边数-2)。
做一做:五边形的内角和是 ,六边形的内角和是 ,八变形的内角和是 。
巩固练习:
1.仔细想,认真填。
(1)在直角三角形中,最大的角是( )度,另外两锐角的和是( )度。
(2)三角形的内角和是( )度。
(3)等边三角形的每个角都是( )度。
(4)一个等腰三角形的顶角是100°,底角应是( )。
(5)在一个三角形中,最多有( )个钝角。
(6)锐角三角形中,任意两个锐角的和一定( )90度。
2.求出三角形各角的度数。
(1)∠1、∠2、∠3是三角形的三个内角,∠1=38°∠2=53°,求∠3的度数。
(2)∠1、∠2是直角三角形中的两个锐角,∠1=50°,求∠2的度数。
3.火眼金睛判对错。
(1)钝角三角形的内角和一定比锐角三角形的内角和大。( )
(2)两个完全相同的直角三角形一定能拼成一个长方形。( )
(3)三角形越大内角和就越大。( )
(4)所有的等边三角形都是锐角三角形。( )
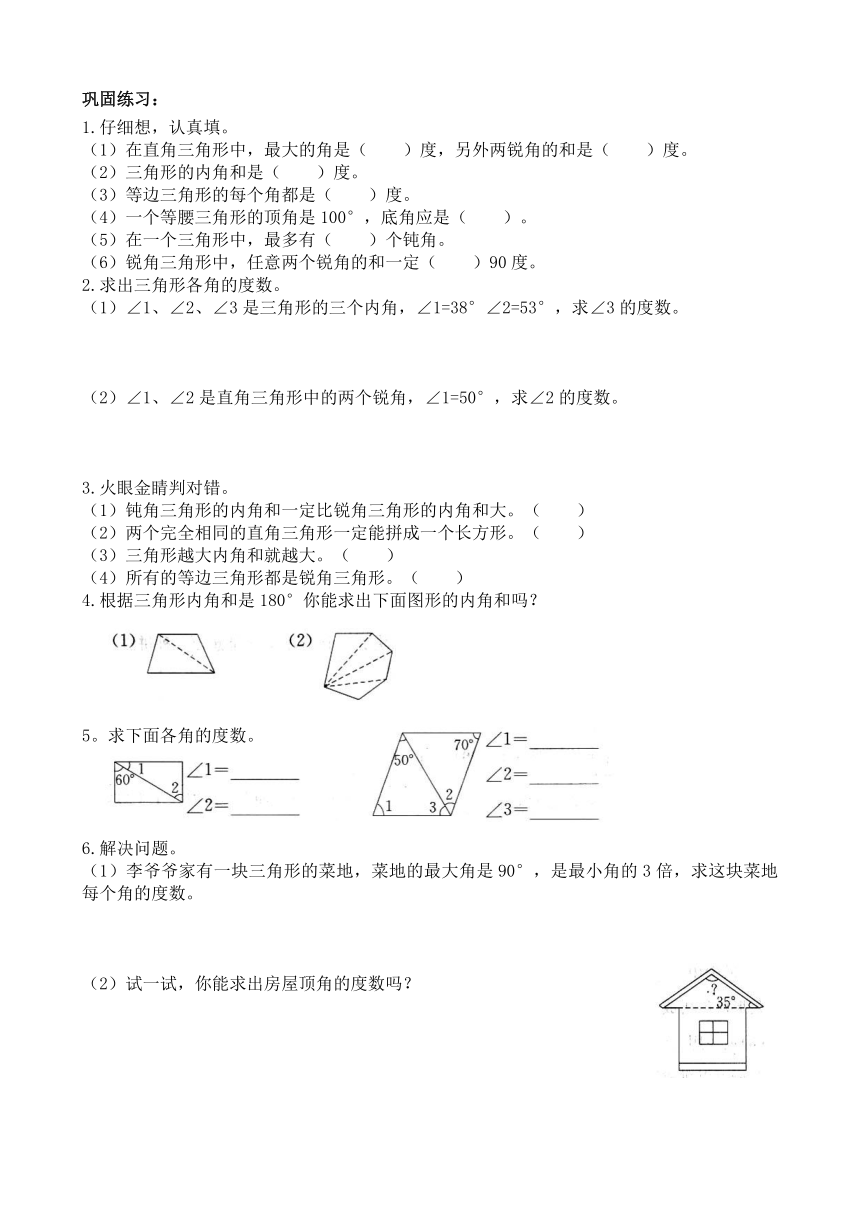
4.根据三角形内角和是180°你能求出下面图形的内角和吗?
5。求下面各角的度数。
6.解决问题。
(1)李爷爷家有一块三角形的菜地,菜地的最大角是90°,是最小角的3倍,求这块菜地每个角的度数。
(2)试一试,你能求出房屋顶角的度数吗?
单元小结:
一、我动脑筋,我会填。
1.三角形按角来分可以分成( )、( )、( );如果按边来边分可以分为( )、( )、( )。
2.三角形具有( )。
3.每个三角形中至少有( )个锐角;最多有( )个直角或钝角。
4.等边三角形的三条边都( ),三个角都是( )。所以等边三角形是( )三角形。
5.每个三角形都有( )条高。
6.三角形的内角都是( )。
7.三角形任意两边之和( )第三边。
8.等腰三角形的两腰( ),( )也相等。
9.一个直角三角形的一个锐角等于45度,另一个锐角等于( ),这个三角形又叫( )。
10.一个等腰三角形,它的一个底角等于70度,它的顶角是( )。
11.在一个三角形中,已知它的两个内角的度数是45度和65度,这个三角形一定是( )三角形。
12.判断下面的三角形是什么三角形,把序号填在相应的括号里。
① ② ③ ④ ⑤ ⑥ ⑦
锐角三角形有( );直角三角形有( );钝角三角形有( );等边三角形有( );等腰三角形有( )。
二、慧眼识真(对的打“√”,错的打“×”)
1.三角形只能有一个直角或一个钝角。 ( )
2.所有的等腰三角形都是锐角三角形。 ( )
3.一个三角形中,最大的角是锐角,那么这个三角形一定是锐角三角形。( )
4.等边三角形一定是锐角三角形。 ( )
5.用三根分别是3厘米、4厘米和7厘米的小棒可以围成一个三角形。( )
对号入座(把正确答案的序号填在括号里)
1.三角形越大,内角和( )
A、越大 B、越小 C、是固定的
2.一个等腰三角形中,基中一底角是75度,顶角是( )。
A、75度 B、45度 C、30度 D、60度
3.一个等腰三角形,底是5厘米,腰是6厘米,它的周长是( )
A、16 B、17 C、15
4.一个等腰三角形的一个底角是65度,这个三角形一定是( )三角形。
A、锐角 B、直角 C、钝角
5.下面各组小棒中能围成三角形的是( )组。
A、3厘米、3厘米、6厘米 B、3厘米、4厘米、5厘米
C、2厘米、3厘米、4厘米
四、填表:(表中∠1、∠2、∠3是三角形的三个内角)
∠1 75。 90。 60。 50。
∠2 65。 120。 60。
∠3 42。 15。 50。
五、解答下面各题。
1.在三角形中,已知∠1=62。,∠2=108。,求∠3。
2.一个直角三角形中,已知其中一个锐角是55。,求另一个锐角是多少度?
3.已知一个等腰三角形的一个顶角是70。,它的每一个底角是多少度?
4.已知一个等腰三角形的一个底角是35°,求其他两个角的度数?
5.已知等腰三角形三边长度之和是62厘米,若一条腰长是22厘米,求它底边的长度。
6.已知正三角形三边长度之和为33厘米,求每边的长?
7. 一块刚刚平整好的三角形田地,量得田地的周长是102m,且∠A=∠B,AB长30m,求AC和BC的长。
8.一块等腰三角形的绿地,它的周长是185m,底边长是53m,腰长是多少米?
9.王霄想做一个等腰三角形形状的风筝。已知两条边长分别是55cm、27cm,第三条边长是多少厘米?
10. 一个三角形的3个内角分别为∠1,∠2,∠3,已知∠2的度数是∠1的2倍,∠3的度数是∠1的3倍,这是一个什么三角形?
11. 一个等腰三角形,其中一个角的度数为70°,求另外两个角的度数。
12.一个等腰三角形,其中一个角的度数为110°,求另外两个角的度数。
六、综合题演练。
1.求出下面长方形、正方形中的∠1,∠2的度数。
2. 求∠1的度数。
① ②
3.已知三角形ABC是等边三角形,∠A=60°,∠1=∠2,∠3=∠4,求∠5的度数。
4. 以点子图中的左边线段为一条边画两个不同的等腰三角形,以右边线段为一条边画两个不同的直角三角形。
5.以图中线段为一条边,画一个等腰直角三角形。
知识引入:
三角形的内角和
例题1:填空。
(1)三角形的内角和是( )。
(2)把三角形三个角剪下来,顶点重合拼在一起可以拼成一个( )角。
(3)在能组成三角形的三个角后面的括号内画“△”,不能组成三角形的画“○”。
90° 42° 58°( )
40° 45° 70°( )
80° 80° 20°( )
125° 35° 20°( )
(4)长方形和正方形的四个角都是( )角,所以长方形和正方形的内角和都是( )。
(5)将任意一个四边形的四个角剪下来,可以拼成一个( )角,所以四边形的内角和是( )。
(6)可以将任意一个四边形分成( )个三角形,四边形的内角和是180°×( )=( )°。
例题2:算一算,判一判。
(1)∠1=50°,∠2=35°,∠3=( ),
这是一个( )三角形。
(2)∠1=42°,∠2=48°,∠3=( ),
这是一个( )三角形。
(3) ∠1=70°,∠2=55°,∠3=( ),
这是一个( )三角形,也是一个( )三角形。
(4)如下图,∠1是直角,∠2=33°,∠3=( )。
(5)等边三角形每个内角都是( )。
例题3:判断。
(1)一个三角形的内角和是180°,用两个完全一样的三角形拼成一个大三角形,这个大三角形的内角和为360°。( )
(2)三角形越大,它的内角和越大。( )
(3)有一个三角形的两个内角分别是91°和89°。( )
例题4:我会算 。
例题5:解决问题我能行 。
(1)四边形的四个内角可以都是锐角吗?可以都是钝角吗?可以都是直角吗?为什么?
(2)在四边形ABCD中,∠A=∠C=90°,∠ABE=∠CBE,∠ADF=∠CDF,则∠ABE+∠FDC等于多少度?
知识精讲:三角形的内角和
1.三角形的内角和:180°
拓展:三角形的一个外角等于它不相邻两个内角的和。
如图:∠4=∠1 + ∠2
三角形内角和的应用:
在三角形中,已知两个角的度数,求第三个角的度数,用内角和180°连续减去已知连个角的度数或减去这两个角的度数和。
3.多边形的内角和
(1)四边形的内角和是360°。
(2)多边形的内角和=180°×(边数-2)。
做一做:五边形的内角和是 ,六边形的内角和是 ,八变形的内角和是 。
巩固练习:
1.仔细想,认真填。
(1)在直角三角形中,最大的角是( )度,另外两锐角的和是( )度。
(2)三角形的内角和是( )度。
(3)等边三角形的每个角都是( )度。
(4)一个等腰三角形的顶角是100°,底角应是( )。
(5)在一个三角形中,最多有( )个钝角。
(6)锐角三角形中,任意两个锐角的和一定( )90度。
2.求出三角形各角的度数。
(1)∠1、∠2、∠3是三角形的三个内角,∠1=38°∠2=53°,求∠3的度数。
(2)∠1、∠2是直角三角形中的两个锐角,∠1=50°,求∠2的度数。
3.火眼金睛判对错。
(1)钝角三角形的内角和一定比锐角三角形的内角和大。( )
(2)两个完全相同的直角三角形一定能拼成一个长方形。( )
(3)三角形越大内角和就越大。( )
(4)所有的等边三角形都是锐角三角形。( )
4.根据三角形内角和是180°你能求出下面图形的内角和吗?
5。求下面各角的度数。
6.解决问题。
(1)李爷爷家有一块三角形的菜地,菜地的最大角是90°,是最小角的3倍,求这块菜地每个角的度数。
(2)试一试,你能求出房屋顶角的度数吗?
单元小结:
一、我动脑筋,我会填。
1.三角形按角来分可以分成( )、( )、( );如果按边来边分可以分为( )、( )、( )。
2.三角形具有( )。
3.每个三角形中至少有( )个锐角;最多有( )个直角或钝角。
4.等边三角形的三条边都( ),三个角都是( )。所以等边三角形是( )三角形。
5.每个三角形都有( )条高。
6.三角形的内角都是( )。
7.三角形任意两边之和( )第三边。
8.等腰三角形的两腰( ),( )也相等。
9.一个直角三角形的一个锐角等于45度,另一个锐角等于( ),这个三角形又叫( )。
10.一个等腰三角形,它的一个底角等于70度,它的顶角是( )。
11.在一个三角形中,已知它的两个内角的度数是45度和65度,这个三角形一定是( )三角形。
12.判断下面的三角形是什么三角形,把序号填在相应的括号里。
① ② ③ ④ ⑤ ⑥ ⑦
锐角三角形有( );直角三角形有( );钝角三角形有( );等边三角形有( );等腰三角形有( )。
二、慧眼识真(对的打“√”,错的打“×”)
1.三角形只能有一个直角或一个钝角。 ( )
2.所有的等腰三角形都是锐角三角形。 ( )
3.一个三角形中,最大的角是锐角,那么这个三角形一定是锐角三角形。( )
4.等边三角形一定是锐角三角形。 ( )
5.用三根分别是3厘米、4厘米和7厘米的小棒可以围成一个三角形。( )
对号入座(把正确答案的序号填在括号里)
1.三角形越大,内角和( )
A、越大 B、越小 C、是固定的
2.一个等腰三角形中,基中一底角是75度,顶角是( )。
A、75度 B、45度 C、30度 D、60度
3.一个等腰三角形,底是5厘米,腰是6厘米,它的周长是( )
A、16 B、17 C、15
4.一个等腰三角形的一个底角是65度,这个三角形一定是( )三角形。
A、锐角 B、直角 C、钝角
5.下面各组小棒中能围成三角形的是( )组。
A、3厘米、3厘米、6厘米 B、3厘米、4厘米、5厘米
C、2厘米、3厘米、4厘米
四、填表:(表中∠1、∠2、∠3是三角形的三个内角)
∠1 75。 90。 60。 50。
∠2 65。 120。 60。
∠3 42。 15。 50。
五、解答下面各题。
1.在三角形中,已知∠1=62。,∠2=108。,求∠3。
2.一个直角三角形中,已知其中一个锐角是55。,求另一个锐角是多少度?
3.已知一个等腰三角形的一个顶角是70。,它的每一个底角是多少度?
4.已知一个等腰三角形的一个底角是35°,求其他两个角的度数?
5.已知等腰三角形三边长度之和是62厘米,若一条腰长是22厘米,求它底边的长度。
6.已知正三角形三边长度之和为33厘米,求每边的长?
7. 一块刚刚平整好的三角形田地,量得田地的周长是102m,且∠A=∠B,AB长30m,求AC和BC的长。
8.一块等腰三角形的绿地,它的周长是185m,底边长是53m,腰长是多少米?
9.王霄想做一个等腰三角形形状的风筝。已知两条边长分别是55cm、27cm,第三条边长是多少厘米?
10. 一个三角形的3个内角分别为∠1,∠2,∠3,已知∠2的度数是∠1的2倍,∠3的度数是∠1的3倍,这是一个什么三角形?
11. 一个等腰三角形,其中一个角的度数为70°,求另外两个角的度数。
12.一个等腰三角形,其中一个角的度数为110°,求另外两个角的度数。
六、综合题演练。
1.求出下面长方形、正方形中的∠1,∠2的度数。
2. 求∠1的度数。
① ②
3.已知三角形ABC是等边三角形,∠A=60°,∠1=∠2,∠3=∠4,求∠5的度数。
4. 以点子图中的左边线段为一条边画两个不同的等腰三角形,以右边线段为一条边画两个不同的直角三角形。
5.以图中线段为一条边,画一个等腰直角三角形。
