人教版四年级数学下册 小数加减法和小数加减混合运算 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版四年级数学下册 小数加减法和小数加减混合运算 同步拓展讲与练+奥数培优(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 679.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 16:58:59 | ||
图片预览


文档简介
小数加减法和小数加减混合运算
知识引入:
一、位数相同的小数加减法
知识精讲1:位数相同的小数加减法
例题1:填空。
(1)小数加法的意义与整数加法的意义( )。
(2)
买一个汉堡和一盒牛奶共需( )元。
(3)小华的身高是1.46米,小明比小华高0.22米,小明的身高是( )米。
(4)比3.14 kg多0.25 kg是( )。
例题2:计算下面各题,并验算。
3.62+8.49= 8.4+12.7=
14.4-3.5= 7.07-5.97=
知识精讲1:位数相同的小数加减法
位数相同的小数加减法的计算方法:
1. 相同数位对齐,也就是小数点对齐。
2. 从末位算起,加法要注意哪一位相加满十,要向前一位进 1 ;减法要注意哪一位不够减,要从前一位退 1 当 10,在本位上加 10 再减。
3. 得数的小数点要与竖式中的小数点对齐。
二、位数不同的小数加减法
例题3:填空。
笔算小数加法时,要把( )对齐,也就是把( )对齐。得数末尾有“0”的,一般要把“0”( )。
例题4:口算。
2.1+0.2= 0.33+0.4= 3.6+1.26= 3.51+0.2= 102+0.3= 12.7+6.09=
例题5:用竖式计算下面各题 ,并验算。
4.5+3.86= 12.36+0.9=
2.57-1.9= 72-6.39=
知识精讲2:位数不同的小数加减法的计算方法
一“添”:根据小数的性质,将位数较少的小数末尾添上0,变成位数相同的小数加减法。
二“算”:依据位数相同的小数加减法的计算方法进行计算。
三“去”:如果得数的小数部分末尾有0,可以将0去掉。
小数加减混合运算
例题6:填空。
(1)小数加减混合运算的顺序与整数加减混合运算的顺序 ( )。
(2)小数加减混合运算的算式里有括号的,要先算( )里面的。
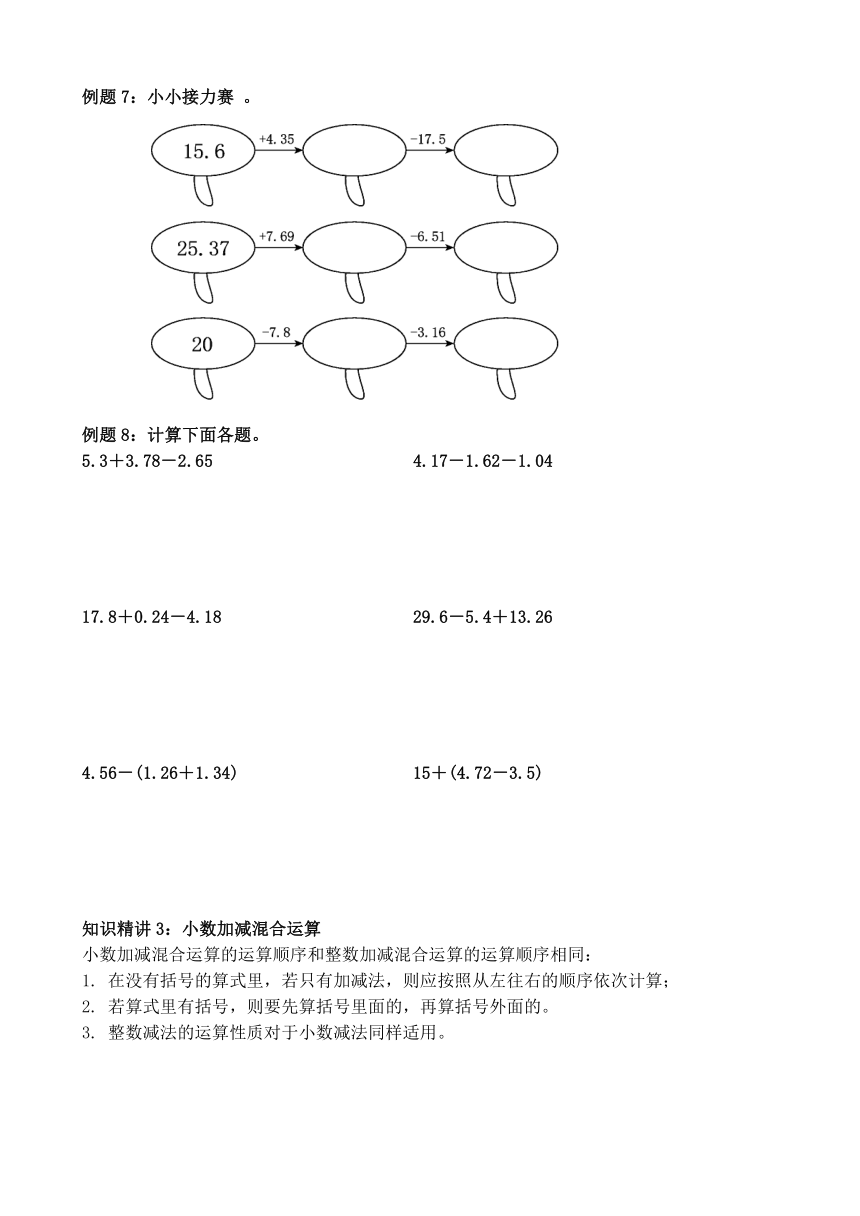
例题7:小小接力赛 。
例题8:计算下面各题。
5.3+3.78-2.65 4.17-1.62-1.04
17.8+0.24-4.18 29.6-5.4+13.26
4.56-(1.26+1.34) 15+(4.72-3.5)
知识精讲3:小数加减混合运算
小数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同:
1. 在没有括号的算式里,若只有加减法,则应按照从左往右的顺序依次计算;
2. 若算式里有括号,则要先算括号里面的,再算括号外面的。
3. 整数减法的运算性质对于小数减法同样适用。
巩固练习(一):小数加减法
1.列式计算,并验算。
9.67+17.48= 98.9-47.68=
验算: 验算:
2.送小动物回家。
3.数学小法官。
改正: 改正:
4.猜猜这个数是多少?
(1)一个数加上5.03就是27.6。
(2)一个数比17.6少0.536。
(3)一个数比3.7多15.78。
5.把下面的分数改成小数,再计算。
- = + =
10- = -=
6.用小数计算。
(1)4千米50米+3千米600米 (2)10吨-3吨5千克
= =
7.解决问题。
(1)一枝钢笔8.45元,一个笔记本比一枝钢笔便宜1.25元,买一个笔记本和一枝钢笔一共需多少元?
(2)小刚和小红两个人的钱比小红的多0.95元,比小刚的多3.46元,小刚和小红两人一共有多少钱?
巩固练习(二):小数加减混合运算
1.口算
3+0.68= 2-0.2= 7-4.5= 6.5-3= 0.9+1.3=
6.5+3= 0.9+1.3= 3-2.4= 6-0.5= 7+4.25=
2.在 里填上“>”“<”或“=”。
4.69+3.02+9.8 4.5+7.8-1.9
10-1.03-4.2 18-4.6+0.02
9.9+9.8+9.7 10.1-0.3-0.4
3.脱式计算。
12-3.8+9.6 19.8-(4.5+7.6) 20.32-4.98+9.6 18-4.6+0.98
4.下面是陈老师家四、五、六月份煤气费、水费、电费一览表。
煤气费 水费 电费 合计
四月份 43.50 36.85 40.75
五月份 17.35 52.73 35.65
六月份 20.35 42.76 39.55
合计
根据上表,你能提出两个数学问题并解答吗?
5.解决问题。
(1)小红的身高是1.36米,比小军矮0.08米,小强比小军矮0.05米,小强的身高是多少米?
(2)把10米长的竹竿插入水池中,竹竿入泥部分是0.36米,露出水面部分是2.27米,水池中水深多少米?
(3)一桶油连桶共重6.5千克,用去一半油后,连桶共重3.5千克,原来油重多少千克?桶重多少千克?
奥数思维拓展:用推理法解决竖式谜问题
1.渗透两种数学思想:推理思想、符号化思想
2.学习两类思维方法:有序思维法、推理法
思维提升:
[例]用1、2、3…9这个9个数字组成算式,已知给出的4个数字,请你补上
其它数字。
[分析]
[解答]
[技巧]
解决竖式谜问题的关键是先分析算式中隐含的数量关系,找准突破口逐一解决,同时还要注意答案往往不唯一。
举一反三:
6.1—0.8
5+0.5
知识引入:
一、位数相同的小数加减法
知识精讲1:位数相同的小数加减法
例题1:填空。
(1)小数加法的意义与整数加法的意义( )。
(2)
买一个汉堡和一盒牛奶共需( )元。
(3)小华的身高是1.46米,小明比小华高0.22米,小明的身高是( )米。
(4)比3.14 kg多0.25 kg是( )。
例题2:计算下面各题,并验算。
3.62+8.49= 8.4+12.7=
14.4-3.5= 7.07-5.97=
知识精讲1:位数相同的小数加减法
位数相同的小数加减法的计算方法:
1. 相同数位对齐,也就是小数点对齐。
2. 从末位算起,加法要注意哪一位相加满十,要向前一位进 1 ;减法要注意哪一位不够减,要从前一位退 1 当 10,在本位上加 10 再减。
3. 得数的小数点要与竖式中的小数点对齐。
二、位数不同的小数加减法
例题3:填空。
笔算小数加法时,要把( )对齐,也就是把( )对齐。得数末尾有“0”的,一般要把“0”( )。
例题4:口算。
2.1+0.2= 0.33+0.4= 3.6+1.26= 3.51+0.2= 102+0.3= 12.7+6.09=
例题5:用竖式计算下面各题 ,并验算。
4.5+3.86= 12.36+0.9=
2.57-1.9= 72-6.39=
知识精讲2:位数不同的小数加减法的计算方法
一“添”:根据小数的性质,将位数较少的小数末尾添上0,变成位数相同的小数加减法。
二“算”:依据位数相同的小数加减法的计算方法进行计算。
三“去”:如果得数的小数部分末尾有0,可以将0去掉。
小数加减混合运算
例题6:填空。
(1)小数加减混合运算的顺序与整数加减混合运算的顺序 ( )。
(2)小数加减混合运算的算式里有括号的,要先算( )里面的。
例题7:小小接力赛 。
例题8:计算下面各题。
5.3+3.78-2.65 4.17-1.62-1.04
17.8+0.24-4.18 29.6-5.4+13.26
4.56-(1.26+1.34) 15+(4.72-3.5)
知识精讲3:小数加减混合运算
小数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同:
1. 在没有括号的算式里,若只有加减法,则应按照从左往右的顺序依次计算;
2. 若算式里有括号,则要先算括号里面的,再算括号外面的。
3. 整数减法的运算性质对于小数减法同样适用。
巩固练习(一):小数加减法
1.列式计算,并验算。
9.67+17.48= 98.9-47.68=
验算: 验算:
2.送小动物回家。
3.数学小法官。
改正: 改正:
4.猜猜这个数是多少?
(1)一个数加上5.03就是27.6。
(2)一个数比17.6少0.536。
(3)一个数比3.7多15.78。
5.把下面的分数改成小数,再计算。
- = + =
10- = -=
6.用小数计算。
(1)4千米50米+3千米600米 (2)10吨-3吨5千克
= =
7.解决问题。
(1)一枝钢笔8.45元,一个笔记本比一枝钢笔便宜1.25元,买一个笔记本和一枝钢笔一共需多少元?
(2)小刚和小红两个人的钱比小红的多0.95元,比小刚的多3.46元,小刚和小红两人一共有多少钱?
巩固练习(二):小数加减混合运算
1.口算
3+0.68= 2-0.2= 7-4.5= 6.5-3= 0.9+1.3=
6.5+3= 0.9+1.3= 3-2.4= 6-0.5= 7+4.25=
2.在 里填上“>”“<”或“=”。
4.69+3.02+9.8 4.5+7.8-1.9
10-1.03-4.2 18-4.6+0.02
9.9+9.8+9.7 10.1-0.3-0.4
3.脱式计算。
12-3.8+9.6 19.8-(4.5+7.6) 20.32-4.98+9.6 18-4.6+0.98
4.下面是陈老师家四、五、六月份煤气费、水费、电费一览表。
煤气费 水费 电费 合计
四月份 43.50 36.85 40.75
五月份 17.35 52.73 35.65
六月份 20.35 42.76 39.55
合计
根据上表,你能提出两个数学问题并解答吗?
5.解决问题。
(1)小红的身高是1.36米,比小军矮0.08米,小强比小军矮0.05米,小强的身高是多少米?
(2)把10米长的竹竿插入水池中,竹竿入泥部分是0.36米,露出水面部分是2.27米,水池中水深多少米?
(3)一桶油连桶共重6.5千克,用去一半油后,连桶共重3.5千克,原来油重多少千克?桶重多少千克?
奥数思维拓展:用推理法解决竖式谜问题
1.渗透两种数学思想:推理思想、符号化思想
2.学习两类思维方法:有序思维法、推理法
思维提升:
[例]用1、2、3…9这个9个数字组成算式,已知给出的4个数字,请你补上
其它数字。
[分析]
[解答]
[技巧]
解决竖式谜问题的关键是先分析算式中隐含的数量关系,找准突破口逐一解决,同时还要注意答案往往不唯一。
举一反三:
6.1—0.8
5+0.5
