第8章-一元一次不等式导学案(无答案)
文档属性
| 名称 | 第8章-一元一次不等式导学案(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 271.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 15:25:20 | ||
图片预览



文档简介
8.1.1 认识不等式
学 习 目 标 了解不等式的概念,会判断一个式子是不是不等式; 了解不等式的解的概念,会判断一个数是不是不等式的解,会根据条件列不等式。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习:P50-52 (1) 李敏的提议是不是真的“浪费”了?__________, (1)买10张票,要付款: (2)买27张票,要付款: (3)买30张票,要付款: (4)比较哪种付款更好? 2、(1)提问:设人数为x人,则应当120<5x时,买30张票合算,剩下的任务是x取哪些数值时,这个不等式成立? (2)完成P51的表格。 (3)从表中可见,当x________时,120﹤5x成立。 (4)当少于30人时,至少要有 ________人进入公园,买30张票反而合算。 例1、用适当符号表示下列关系。(1)a的7倍与15的和比b的3倍大: _______________________(2)a是非负数; _______________________(3)x比y大3. _______________________ (4)a是正数; _______________________(5)a是负数; _______________________(6)a与6的和不大于5; _______________________ (7)x与2的差不小于-1; _______________________(8)x的4倍大于7; _______________________(9)y的一半小于3. _______________________例2 判断下列各数哪些是不等式2x-1<5的解? -6,-5,-2,0,1.5,4.5,6。 例3、不等式x≤3的正整数解是______________________; 不等式x<3的非负整数解是 ________________________; 不等式x<3的自然数解是 ________________________; 不等式x>-2的负整数解有 _________________________。 一、随堂笔记1、不等式的定义:用不等号“<”(或“≤”),“>”(或“≥”),“≠”表示 的式子,叫做不等式。2、_______________________ _________,叫做不等式的解。二、同步演练1、判断下列各式哪些是等式、哪些是不等式?(填序号) x+y ; ②3x>7; 5=2+3 ; ④x>0 ; ⑤ 2x-3 ⑥2x-3y≥1 ; ⑦ 52。答:等式 _______________;不等式 ________________。2、用不等式表示:(1)x的与3的差大于2; 答:______________________ (2)2x与1的和小于零; 答:______________________ (3)a的2倍与4的差是正数; 答:______________________ (4)b的与c的和是负数; 答:______________________ (5)a与b的差是非负数; 答:______________________ (6)x的绝对值与1的和不小于1。 答:______________________ 3、判断下列各数中,哪些是不等式x+2>5的解? -3, -2, -1, 0, 1.5, 2.5, 3,3.5, 5, 7。
8.2.1 不等式的解集
学 习 目 标 1、理解不等式的解集这个概念,了解解不等式的概念; 2、会在数轴上表示不等式的解集。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习:P53-541、在下列这组数中: -3,-2,-1, 0 ,1.5 ,2.5 ,3 ,3.5 ,5, 7 哪些是不等式x+2>5的解,哪些不是?答: 是不等式x+2>5的解; 不是不等式x+2>5的解; 2、你发现了什么规律,不等式x+2>5的解满足什么条件? 3、这个不等式的解集可以表示为: 4、不等式的解集也可以在数轴上直观的表示出来,请在数轴上表示这个不等式的解集: 5、试一试:用上面的方法猜想一下不等式的解集是: 在数轴上表示这个不等式的解集: 6、思考:这两个不等式的解集在数轴上的表示有什么不同?你发现了什么规律? 例1、判断下列不等式的解集是否正确,为什么? (1) 2x>2的解集是x>-2; (2) 1-3x<-5的解集是x>5 例2、数轴上表示下列不等式的解集:(1)x≥-2, (2)x<4, (3)x≤4 例3.不等式-2学 习 目 标 1、掌握不等式的三个基本性质; 2、运用不等式的三个性质对不等式变形。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
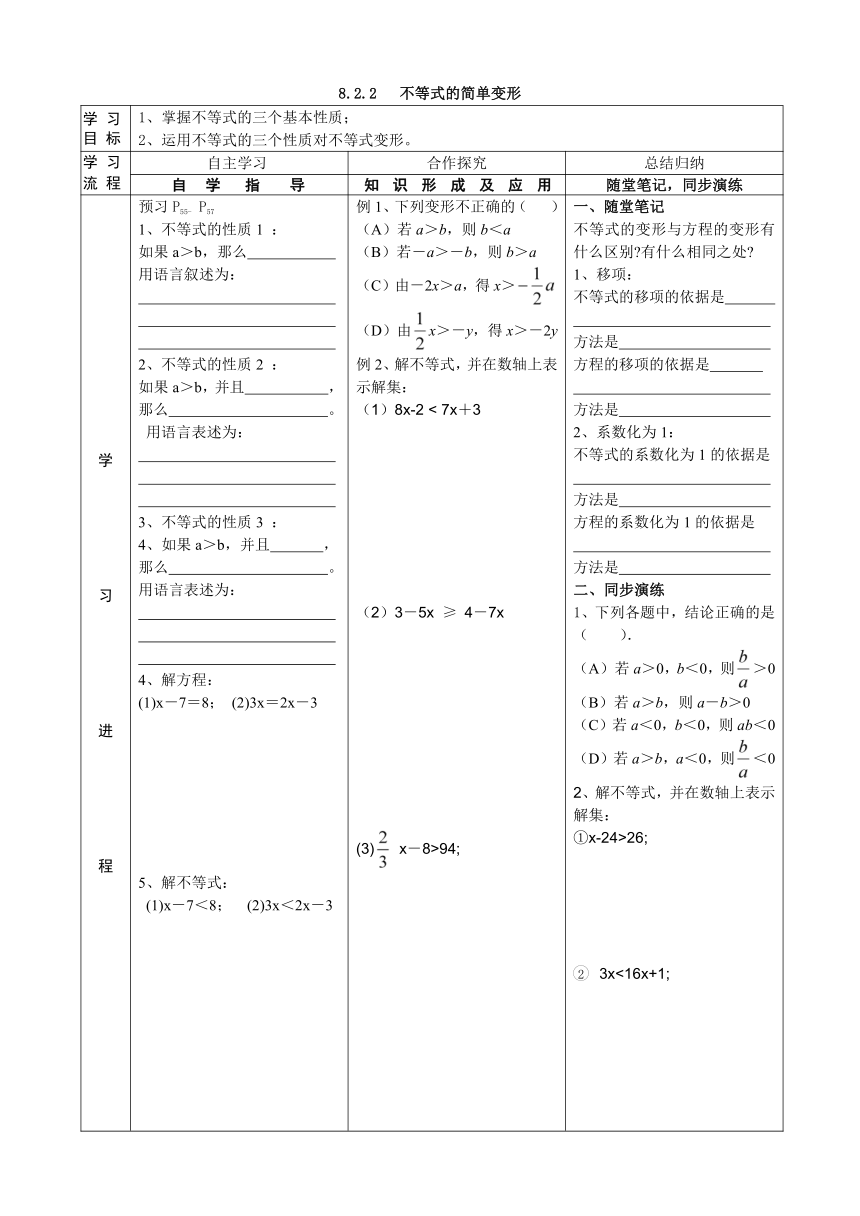
学 习 进 程 预习P55- P571、不等式的性质1 : 如果a>b,那么 用语言叙述为: 2、不等式的性质2 : 如果a>b,并且 ,那么 。 用语言表述为: 不等式的性质3 : 如果a>b,并且 ,那么 。 用语言表述为: 4、解方程: (1)x-7=8; (2)3x=2x-3 5、解不等式: (1)x-7<8; (2)3x<2x-3 例1、下列变形不正确的( ) (A)若a>b,则b<a (B)若-a>-b,则b>a (C)由-2x>a,得x>(D)由x>-y,得x>-2y 例2、解不等式,并在数轴上表示解集:(1)8x-2 < 7x+3 (2)3-5x ≥ 4-7x (3) x-8>94; 一、随堂笔记不等式的变形与方程的变形有什么区别?有什么相同之处? 1、移项: 不等式的移项的依据是 方法是 方程的移项的依据是 方法是 2、系数化为1: 不等式的系数化为1的依据是 方法是 方程的系数化为1的依据是 方法是 二、同步演练 1、下列各题中,结论正确的是 ( ). 若a>0,b<0,则>0 若a>b,则a-b>0 (C)若a<0,b<0,则ab<0 (D)若a>b,a<0,则<02、解不等式,并在数轴上表示解集:①x-24>26; 3x<16x+1;
8.2.2 不等式的简单变形
8.2.3 解一元一次不等式(1)
学 习 目 标 1、了解一元一次不等式的概念; 2、掌握解一元一次不等式的方法。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习P55- P57 1、解下列不等式,并将解集在数轴上表示出来。 (1)2x-1<4x+13; (2)2(5x+3)≤x-3(1-2x)。 2、解不等式 解:去分母,得 去括号,得 移项,得 合并同类项,得 系数化为1,得 例1.解下列不等式,并将解集在数轴上表示出来。(1) (2) (1-2x)> 例2、当x取何值时,代数式的值与的差不大于1? 一、随堂笔记: 解不等式的基本步骤: (1) ;(2) ;(3) ; (4) ; (5) 。 二、同步演练: 1、下面的解法对不对吗? ①由-x=5,得x=-5; ②由-x>5,得x>-5; ③由2x>-4,得x<-2; ④由-x≤3,得x≥-6。 2、解不等式
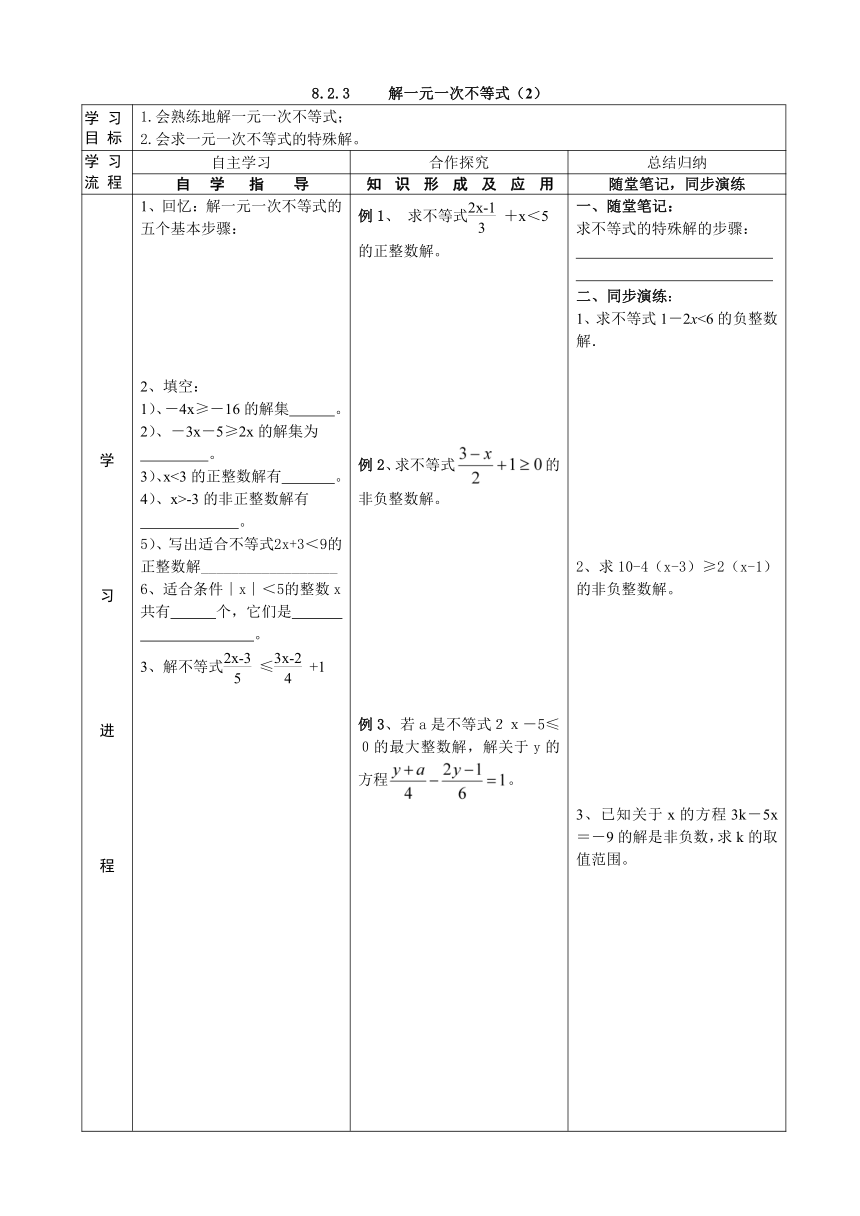
8.2.3 解一元一次不等式(2)
学 习 目 标 1.会熟练地解一元一次不等式; 2.会求一元一次不等式的特殊解。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 1、回忆:解一元一次不等式的五个基本步骤: 2、填空:1)、-4x≥-16的解集 。 2)、-3x-5≥2x的解集为 。 3)、x<3的正整数解有 。 4)、x>-3的非正整数解有 。5)、写出适合不等式2x+3<9的正整数解__________________6、适合条件∣x∣<5的整数x共有 个,它们是 。 3、解不等式≤+1 例1、 求不等式+x<5的正整数解。 例2、求不等式的非负整数解。 例3、若a是不等式2x-5≤0的最大整数解,解关于y的方程。 一、随堂笔记:求不等式的特殊解的步骤: 二、同步演练:1、求不等式1-2x<6的负整数解. 2、求10-4(x-3)≥2(x-1)的非负整数解。 3、已知关于x的方程3k-5x=-9的解是非负数,求k的取值范围。
8.3.1 一元一次不等式组(一)
学 习 目 标 了解一元一次不等式组的解集的概念; 2、会解一元一次不等式组,并把解集在数轴上表示出来;
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习:P62-P65回答下列问题 1、问题:用每分钟可抽水30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不超过1500吨,那么需要多少时间能将污水抽完? 2、分析: (1)设需要x分钟能将污水抽完,那么总的抽水量为 (2)题中的不等关系有: (3)根据不关系,可列不等式: (4)分别求出两个不等式的解集: (4)在同一数轴上表示出这两个不等式的解集: (5)问题的答案是: 3、概括: (1)一元一次不等式组: (2)一元一次不等式组的解集: 例1、解不等式组: 例2、求不等式组:的整数解 例3、解不等式: 一、随堂笔记: 解一元一次不等式组的一般步骤: (1) (2) (3) 二、同步演练: 解下列不等式组,写出满足条件的所有整数解 (1) (2) (3)
8.3.2 一元一次不等式组(二)
学 习 目 标 1、探索一元一次方程组解集的规律; 2、能利用一元一次不等式组解集的规律,直接写出不等式组的解集;
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 (1)完成下面填表:不等式组 图示 解集 不等式组 图示 解集 不等式组及其解集有何特点,你能把它推广到一般吗?(a>b)不等式组 图示 解集 不等式组 图示 解集 (3)你能用一句话来概括一元一次不等式组解集的规律吗? 例1、不画数轴解下列不等式组: (1) (2) (3) 一、随堂笔记: 一元一次不等式组解集的规律: 二、同步演练:1、解下列不等式组: (1) (2) (3)
8.3.3 一元一次不等式组(三)
学 习 目 标 1、已知一元一次不等式组的解集,会求字母的取值范围;
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 1、回顾:一元一次不等式组解集的规律: 2、探索: 已知关于x不等式组: (1)当时,解这个不等式组, (2)当时,解这个不等式组, 3、思考: 当a取何值时,不等式组有解;当a取何值时,不等式组有解? 例1、已知关于x的不等式组 (1)若不等式组无解,求m的取值范围 (2)若不等式组有解,求m的取值范围 (3)若不等式组有1个整数解,求m的取值范围 (4)若不等式组有3个整数解,求m的取值范围 一、随堂笔记:已知一元一次不等式组的解集,求字母取值范围的一般步骤是: (1) (2) (3) 二、同步演练: 1、若不等式组的解集为,求的取值范围 2、若不等式组无解,求的取值范围
8.3.4 一元一次不等式组(四)
学 习 目 标 会列一元一次不等式(组)解决实际问题
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习P60提出的问题: 在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每道题,答对得10分,答错或不答扣5分,总得分不少于80分者能通过预选赛,通过者至少应答对多少道题?有哪些可能情形? (1)题中的等量关系为: (2)题中的不等关系为: (3)若设答对了x道题,则答错了 道题,得分为 (4)根据不等关系可列不等式为: (5)解得: (6)实际问题的答案是: (7)试一试:一堆玩具分给若干个小朋友,若每人分3件,则剩余4件,若前面每人分4件,则最后一人得到的玩具最多3件,问小朋友的人数至少有多少人? 例1、某校校长暑假将带领该校“三好学生”去三峡旅游,甲旅行社说:如果校长买全票一张,则其余学生可享受半价优惠;乙旅行社说:包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元,至少要多少名学生选甲旅行社比较好? 例2、将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只。问有笼多少个?有鸡多少只? 一、随堂笔记:列一元一次不等式(组)解决实际问题的一般步骤是: (1) (2) (3) (4) (5) (6) 二、同步演练:1、爆破施工时,导火索燃烧的速度是0.8cm/s,人跑开的速度是5m/s,为了使点火的战士在施工时能跑到100m以外的安全地区,导火索至少需要多长? 2、用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨;若每辆汽车装满8吨,则最后一辆汽车不满也不空,问有多少辆汽车?
8.3.5 一元一次不等式组(五)
学 习 目 标 会列一元一次不等式组解决方案设计问题
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本. (1)符合题意的组建方案有几种?请你帮学校设计出来; (2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?思路引导: (1)题中的等量关系是: (2)题中的不等关系是: (3)设组建中型图书角为x个,则组建中型图书角为 个; (4)根据不等关系可列不等式组为: (5)解得: (6)不等式组的整数解有: (7)组建的方案有: (8)计算每种方案的费用: (9)费用最低方案是: 例1、在中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元?(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低. 同步演练:某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个 种造型需甲种花卉50盆,乙种花卉90盆. (1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来. (2)若搭配一个 种造型的成本是800元,搭配一个 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
1
学 习 目 标 了解不等式的概念,会判断一个式子是不是不等式; 了解不等式的解的概念,会判断一个数是不是不等式的解,会根据条件列不等式。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习:P50-52 (1) 李敏的提议是不是真的“浪费”了?__________, (1)买10张票,要付款: (2)买27张票,要付款: (3)买30张票,要付款: (4)比较哪种付款更好? 2、(1)提问:设人数为x人,则应当120<5x时,买30张票合算,剩下的任务是x取哪些数值时,这个不等式成立? (2)完成P51的表格。 (3)从表中可见,当x________时,120﹤5x成立。 (4)当少于30人时,至少要有 ________人进入公园,买30张票反而合算。 例1、用适当符号表示下列关系。(1)a的7倍与15的和比b的3倍大: _______________________(2)a是非负数; _______________________(3)x比y大3. _______________________ (4)a是正数; _______________________(5)a是负数; _______________________(6)a与6的和不大于5; _______________________ (7)x与2的差不小于-1; _______________________(8)x的4倍大于7; _______________________(9)y的一半小于3. _______________________例2 判断下列各数哪些是不等式2x-1<5的解? -6,-5,-2,0,1.5,4.5,6。 例3、不等式x≤3的正整数解是______________________; 不等式x<3的非负整数解是 ________________________; 不等式x<3的自然数解是 ________________________; 不等式x>-2的负整数解有 _________________________。 一、随堂笔记1、不等式的定义:用不等号“<”(或“≤”),“>”(或“≥”),“≠”表示 的式子,叫做不等式。2、_______________________ _________,叫做不等式的解。二、同步演练1、判断下列各式哪些是等式、哪些是不等式?(填序号) x+y ; ②3x>7; 5=2+3 ; ④x>0 ; ⑤ 2x-3 ⑥2x-3y≥1 ; ⑦ 52。答:等式 _______________;不等式 ________________。2、用不等式表示:(1)x的与3的差大于2; 答:______________________ (2)2x与1的和小于零; 答:______________________ (3)a的2倍与4的差是正数; 答:______________________ (4)b的与c的和是负数; 答:______________________ (5)a与b的差是非负数; 答:______________________ (6)x的绝对值与1的和不小于1。 答:______________________ 3、判断下列各数中,哪些是不等式x+2>5的解? -3, -2, -1, 0, 1.5, 2.5, 3,3.5, 5, 7。
8.2.1 不等式的解集
学 习 目 标 1、理解不等式的解集这个概念,了解解不等式的概念; 2、会在数轴上表示不等式的解集。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习:P53-541、在下列这组数中: -3,-2,-1, 0 ,1.5 ,2.5 ,3 ,3.5 ,5, 7 哪些是不等式x+2>5的解,哪些不是?答: 是不等式x+2>5的解; 不是不等式x+2>5的解; 2、你发现了什么规律,不等式x+2>5的解满足什么条件? 3、这个不等式的解集可以表示为: 4、不等式的解集也可以在数轴上直观的表示出来,请在数轴上表示这个不等式的解集: 5、试一试:用上面的方法猜想一下不等式的解集是: 在数轴上表示这个不等式的解集: 6、思考:这两个不等式的解集在数轴上的表示有什么不同?你发现了什么规律? 例1、判断下列不等式的解集是否正确,为什么? (1) 2x>2的解集是x>-2; (2) 1-3x<-5的解集是x>5 例2、数轴上表示下列不等式的解集:(1)x≥-2, (2)x<4, (3)x≤4 例3.不等式-2
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习P55- P571、不等式的性质1 : 如果a>b,那么 用语言叙述为: 2、不等式的性质2 : 如果a>b,并且 ,那么 。 用语言表述为: 不等式的性质3 : 如果a>b,并且 ,那么 。 用语言表述为: 4、解方程: (1)x-7=8; (2)3x=2x-3 5、解不等式: (1)x-7<8; (2)3x<2x-3 例1、下列变形不正确的( ) (A)若a>b,则b<a (B)若-a>-b,则b>a (C)由-2x>a,得x>(D)由x>-y,得x>-2y 例2、解不等式,并在数轴上表示解集:(1)8x-2 < 7x+3 (2)3-5x ≥ 4-7x (3) x-8>94; 一、随堂笔记不等式的变形与方程的变形有什么区别?有什么相同之处? 1、移项: 不等式的移项的依据是 方法是 方程的移项的依据是 方法是 2、系数化为1: 不等式的系数化为1的依据是 方法是 方程的系数化为1的依据是 方法是 二、同步演练 1、下列各题中,结论正确的是 ( ). 若a>0,b<0,则>0 若a>b,则a-b>0 (C)若a<0,b<0,则ab<0 (D)若a>b,a<0,则<02、解不等式,并在数轴上表示解集:①x-24>26; 3x<16x+1;
8.2.2 不等式的简单变形
8.2.3 解一元一次不等式(1)
学 习 目 标 1、了解一元一次不等式的概念; 2、掌握解一元一次不等式的方法。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习P55- P57 1、解下列不等式,并将解集在数轴上表示出来。 (1)2x-1<4x+13; (2)2(5x+3)≤x-3(1-2x)。 2、解不等式 解:去分母,得 去括号,得 移项,得 合并同类项,得 系数化为1,得 例1.解下列不等式,并将解集在数轴上表示出来。(1) (2) (1-2x)> 例2、当x取何值时,代数式的值与的差不大于1? 一、随堂笔记: 解不等式的基本步骤: (1) ;(2) ;(3) ; (4) ; (5) 。 二、同步演练: 1、下面的解法对不对吗? ①由-x=5,得x=-5; ②由-x>5,得x>-5; ③由2x>-4,得x<-2; ④由-x≤3,得x≥-6。 2、解不等式
8.2.3 解一元一次不等式(2)
学 习 目 标 1.会熟练地解一元一次不等式; 2.会求一元一次不等式的特殊解。
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 1、回忆:解一元一次不等式的五个基本步骤: 2、填空:1)、-4x≥-16的解集 。 2)、-3x-5≥2x的解集为 。 3)、x<3的正整数解有 。 4)、x>-3的非正整数解有 。5)、写出适合不等式2x+3<9的正整数解__________________6、适合条件∣x∣<5的整数x共有 个,它们是 。 3、解不等式≤+1 例1、 求不等式+x<5的正整数解。 例2、求不等式的非负整数解。 例3、若a是不等式2x-5≤0的最大整数解,解关于y的方程。 一、随堂笔记:求不等式的特殊解的步骤: 二、同步演练:1、求不等式1-2x<6的负整数解. 2、求10-4(x-3)≥2(x-1)的非负整数解。 3、已知关于x的方程3k-5x=-9的解是非负数,求k的取值范围。
8.3.1 一元一次不等式组(一)
学 习 目 标 了解一元一次不等式组的解集的概念; 2、会解一元一次不等式组,并把解集在数轴上表示出来;
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习:P62-P65回答下列问题 1、问题:用每分钟可抽水30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不超过1500吨,那么需要多少时间能将污水抽完? 2、分析: (1)设需要x分钟能将污水抽完,那么总的抽水量为 (2)题中的不等关系有: (3)根据不关系,可列不等式: (4)分别求出两个不等式的解集: (4)在同一数轴上表示出这两个不等式的解集: (5)问题的答案是: 3、概括: (1)一元一次不等式组: (2)一元一次不等式组的解集: 例1、解不等式组: 例2、求不等式组:的整数解 例3、解不等式: 一、随堂笔记: 解一元一次不等式组的一般步骤: (1) (2) (3) 二、同步演练: 解下列不等式组,写出满足条件的所有整数解 (1) (2) (3)
8.3.2 一元一次不等式组(二)
学 习 目 标 1、探索一元一次方程组解集的规律; 2、能利用一元一次不等式组解集的规律,直接写出不等式组的解集;
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 (1)完成下面填表:不等式组 图示 解集 不等式组 图示 解集 不等式组及其解集有何特点,你能把它推广到一般吗?(a>b)不等式组 图示 解集 不等式组 图示 解集 (3)你能用一句话来概括一元一次不等式组解集的规律吗? 例1、不画数轴解下列不等式组: (1) (2) (3) 一、随堂笔记: 一元一次不等式组解集的规律: 二、同步演练:1、解下列不等式组: (1) (2) (3)
8.3.3 一元一次不等式组(三)
学 习 目 标 1、已知一元一次不等式组的解集,会求字母的取值范围;
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 1、回顾:一元一次不等式组解集的规律: 2、探索: 已知关于x不等式组: (1)当时,解这个不等式组, (2)当时,解这个不等式组, 3、思考: 当a取何值时,不等式组有解;当a取何值时,不等式组有解? 例1、已知关于x的不等式组 (1)若不等式组无解,求m的取值范围 (2)若不等式组有解,求m的取值范围 (3)若不等式组有1个整数解,求m的取值范围 (4)若不等式组有3个整数解,求m的取值范围 一、随堂笔记:已知一元一次不等式组的解集,求字母取值范围的一般步骤是: (1) (2) (3) 二、同步演练: 1、若不等式组的解集为,求的取值范围 2、若不等式组无解,求的取值范围
8.3.4 一元一次不等式组(四)
学 习 目 标 会列一元一次不等式(组)解决实际问题
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 预习P60提出的问题: 在“科学与艺术”知识竞赛的预选赛中共有20道题,对于每道题,答对得10分,答错或不答扣5分,总得分不少于80分者能通过预选赛,通过者至少应答对多少道题?有哪些可能情形? (1)题中的等量关系为: (2)题中的不等关系为: (3)若设答对了x道题,则答错了 道题,得分为 (4)根据不等关系可列不等式为: (5)解得: (6)实际问题的答案是: (7)试一试:一堆玩具分给若干个小朋友,若每人分3件,则剩余4件,若前面每人分4件,则最后一人得到的玩具最多3件,问小朋友的人数至少有多少人? 例1、某校校长暑假将带领该校“三好学生”去三峡旅游,甲旅行社说:如果校长买全票一张,则其余学生可享受半价优惠;乙旅行社说:包括校长在内全部按全票的6折优惠。已知两家旅行社的全票价都是240元,至少要多少名学生选甲旅行社比较好? 例2、将不足40只鸡放入若干个笼中,若每个笼里放4只,则有一只鸡无笼可放;若每个笼里放5只,则有一笼无鸡可放,且最后一笼不足3只。问有笼多少个?有鸡多少只? 一、随堂笔记:列一元一次不等式(组)解决实际问题的一般步骤是: (1) (2) (3) (4) (5) (6) 二、同步演练:1、爆破施工时,导火索燃烧的速度是0.8cm/s,人跑开的速度是5m/s,为了使点火的战士在施工时能跑到100m以外的安全地区,导火索至少需要多长? 2、用若干辆载重量为8吨的汽车运一批货物,若每辆汽车只装4吨,则剩下20吨;若每辆汽车装满8吨,则最后一辆汽车不满也不空,问有多少辆汽车?
8.3.5 一元一次不等式组(五)
学 习 目 标 会列一元一次不等式组解决方案设计问题
学 习 流 程 自主学习 合作探究 总结归纳
自 学 指 导 知 识 形 成 及 应 用 随堂笔记,同步演练
学 习 进 程 某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本. (1)符合题意的组建方案有几种?请你帮学校设计出来; (2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?思路引导: (1)题中的等量关系是: (2)题中的不等关系是: (3)设组建中型图书角为x个,则组建中型图书角为 个; (4)根据不等关系可列不等式组为: (5)解得: (6)不等式组的整数解有: (7)组建的方案有: (8)计算每种方案的费用: (9)费用最低方案是: 例1、在中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.(1)求每台电脑、每台电子白板各多少万元?(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低. 同步演练:某县筹备20周年县庆,园林部门决定利用现有的3490盆甲种花卉和2950盆乙种花卉搭配 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个 种造型需甲种花卉50盆,乙种花卉90盆. (1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来. (2)若搭配一个 种造型的成本是800元,搭配一个 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
1
