19.3.1 课题学习 选择方案(共24张PPT)
文档属性
| 名称 | 19.3.1 课题学习 选择方案(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 220.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 15:22:23 | ||
图片预览



文档简介
(共21张PPT)
人教版 八年级数学下册
第19章 一次函数
19.3.1 课题学习 选择方案
学习目标:
1.会用一次函数知识解决方案选择问题,体会函数
模型思想;
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方
法.
学习重点:
建立函数模型解决方案选择问题.
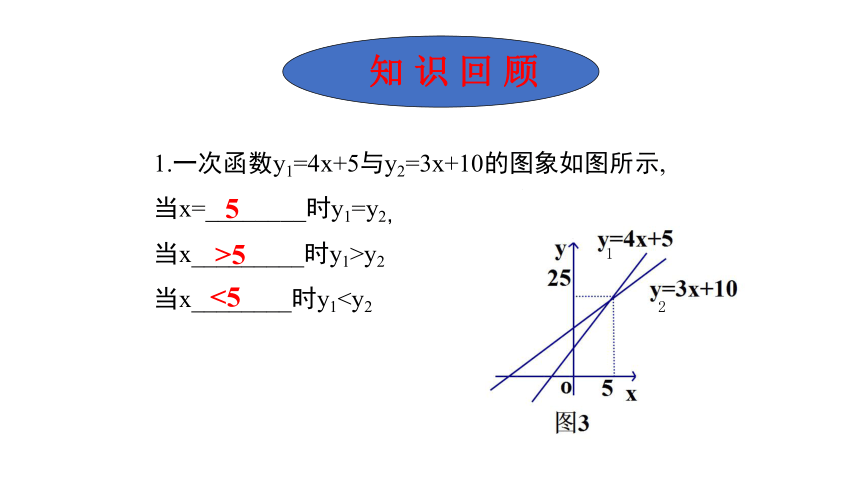
1.一次函数y1=4x+5与y2=3x+10的图象如图所示,
当x=________时y1=y2,
当x_________时y1>y2
当x________时y11
2
知 识 回 顾
>5
<5
5
1
2
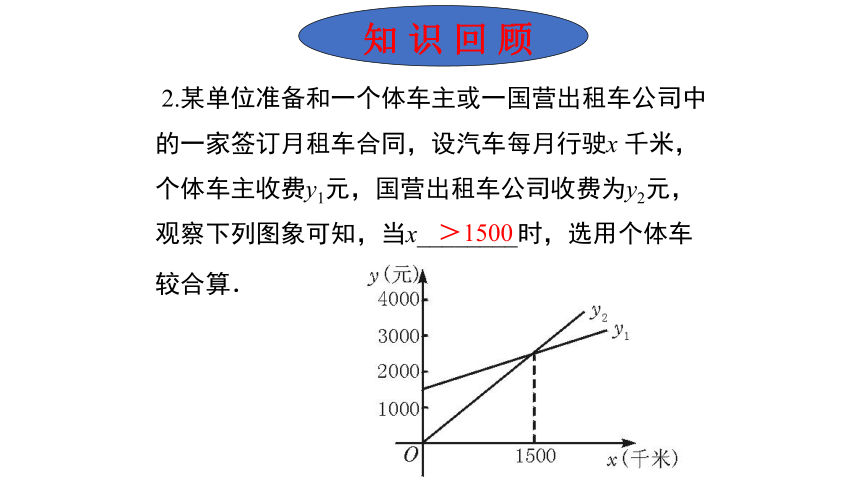
2.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
知 识 回 顾
一件事情,有时会有不同的实施方案
A 方案 B 方案 C 方案 D 方案
选择方案时,常用到一次函数选择最优方案
情 景 导 入
选择方案
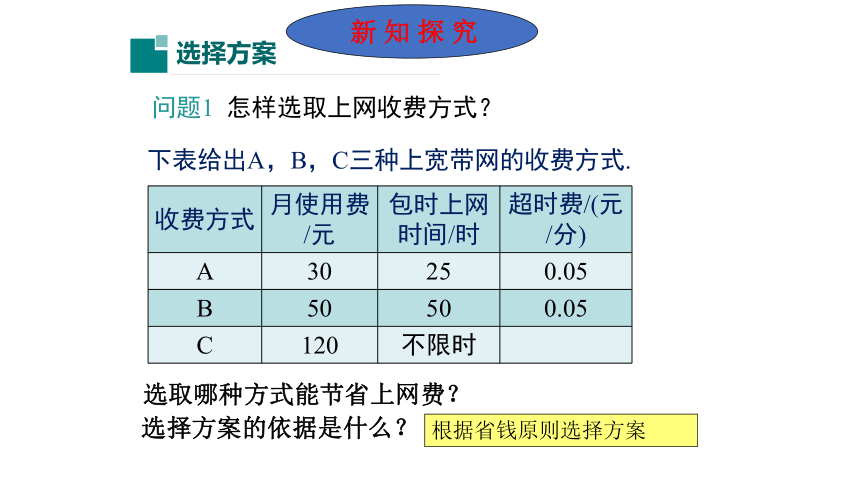
问题1 怎样选取上网收费方式?
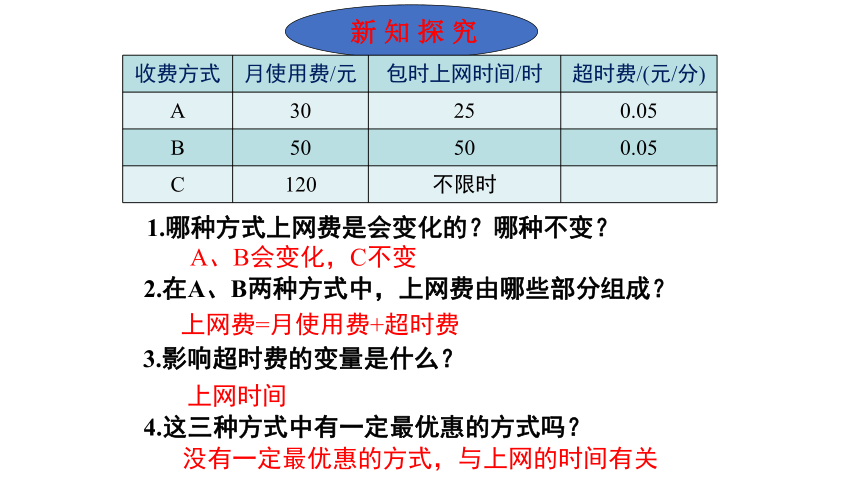
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
新 知 探 究
选取哪种方式能节省上网费?
根据省钱原则选择方案
选择方案的依据是什么?
新 知 探 究
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
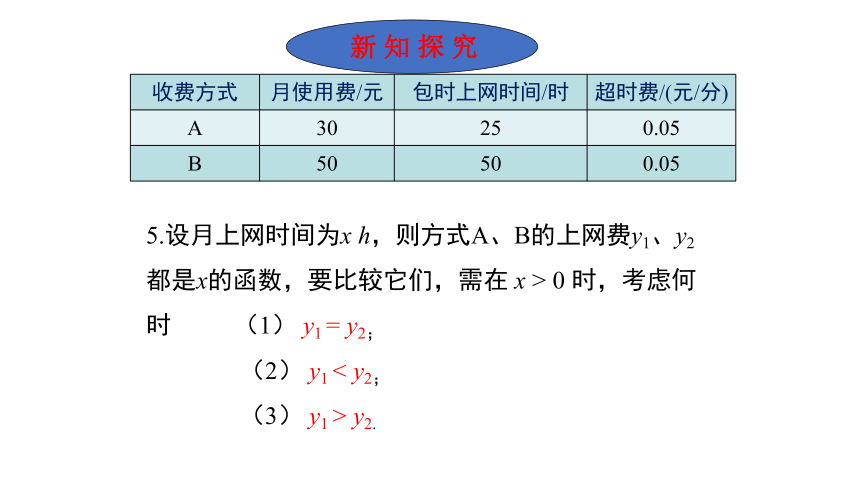
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
5.设月上网时间为x h,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时 (1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
新 知 探 究
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
6.在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
新 知 探 究
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
7.你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
当x≥0时,y3=120.
新 知 探 究
方式A.
新 知 探 究
方式B.
方式C. 请比较y1 y2 y3 的大小?
当x≥0时,y3=120.
这个问题看起来还是有点复杂,难点在于每一个函数的解析式都是分类表示的,需要分类讨论,而怎样分类是难点,怎么办?
综上分析我们把这个问题描述为函数问题,设上网时间为 X,方案A,B,C的上网费用分别为y1 元,y2 元, y3 元,且
——先画出图象看看.
方式A.
在同一坐标系画出它们的图象:
新 知 探 究
方式B.
方式C.
当x≥0时,y3=120.
7.当上网时__________时,选择方式A最省钱.
在同一坐标系画出它们的图象:
新 知 探 究
此时,A和B方式一样省钱
7.当上网时__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
在同一坐标系画出它们的图象:
新 知 探 究
此时,B和C方式一样省钱
7.当上网时__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
在同一坐标系画出它们的图象:
新 知 探 究
实际问题
一次函数问题
设变量
找对应关系
一次函数问题的解
实际问题的解
解释实
际意义
这个实际问题的解决过程中是怎样思考的?
解 后 反 思
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费为0.2元/分;
B方案: 零月租费,通话费为0.3元/分.
(1)试写出A,B两种方案所付话费y(元)与通话 时间t(分)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出哪种付费方式合算?
练 习 巩 固
A方案: y1 = 15+0.2t(t≥0)
B方案:y2 = 0.3t(t≥0).
解:(1) A方案: y1 = 15+0.2t(t≥0),
B方案:
y2 = 0.3t(t≥0).
(2)这两个函数的图象如下:
t(分)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y1 = 15+0.2t
y2 = 0.3t
●
观察图象,可知:
当通话时间为150分时,选择A或B方案费用一样;
当通话时间少于150分时,选择B方案费合算;
当通话时间多于150分时,选择A方案合算.
练 习 巩 固
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
课 堂 小 结
1.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法, 其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
课 后 作 业
2. 东风商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元.该商场为了促销制定了两种优惠方案供顾客选择.
甲:买一支毛笔赠送一本书法练习本.
乙:按购买金额打九折付款.
某校欲为校书法兴趣组购买这种毛笔10支,书法练习本x(x≤10)本.如何选择方案购买呢?
课 后 作 业
人教版 八年级数学下册
第19章 一次函数
19.3.1 课题学习 选择方案
学习目标:
1.会用一次函数知识解决方案选择问题,体会函数
模型思想;
2.能从不同的角度思考问题,优化解决问题的方法;
3.能进行解决问题过程的反思,总结解决问题的方
法.
学习重点:
建立函数模型解决方案选择问题.
1.一次函数y1=4x+5与y2=3x+10的图象如图所示,
当x=________时y1=y2,
当x_________时y1>y2
当x________时y1
2
知 识 回 顾
>5
<5
5
1
2
2.某单位准备和一个体车主或一国营出租车公司中的一家签订月租车合同,设汽车每月行驶x 千米,个体车主收费y1元,国营出租车公司收费为y2元,观察下列图象可知,当x________时,选用个体车较合算.
>1500
知 识 回 顾
一件事情,有时会有不同的实施方案
A 方案 B 方案 C 方案 D 方案
选择方案时,常用到一次函数选择最优方案
情 景 导 入
选择方案
问题1 怎样选取上网收费方式?
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
下表给出A,B,C三种上宽带网的收费方式.
新 知 探 究
选取哪种方式能节省上网费?
根据省钱原则选择方案
选择方案的依据是什么?
新 知 探 究
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
1.哪种方式上网费是会变化的?哪种不变?
A、B会变化,C不变
2.在A、B两种方式中,上网费由哪些部分组成?
上网费=月使用费+超时费
3.影响超时费的变量是什么?
上网时间
4.这三种方式中有一定最优惠的方式吗?
没有一定最优惠的方式,与上网的时间有关
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
5.设月上网时间为x h,则方式A、B的上网费y1、y2都是x的函数,要比较它们,需在 x > 0 时,考虑何时 (1) y1 = y2;
(2) y1 < y2;
(3) y1 > y2.
新 知 探 究
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
6.在方式A中,超时费一定会产生吗?什么情况下才会有超时费?
不一定,只有在上网时间超过25小时时才会产生.
合起来可写为:
当0≤x≤25时,y1=30;
当x>25时,y1=30+0.05×60(x-25)=3x-45.
新 知 探 究
收费方式 月使用费/元 包时上网时间/时 超时费/(元/分)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
7.你能自己写出方式B的上网费y2关于上网时间 x之间的函数关系式吗
方式C的上网费y3关于上网时间x之间的函数关系式呢
当x≥0时,y3=120.
新 知 探 究
方式A.
新 知 探 究
方式B.
方式C. 请比较y1 y2 y3 的大小?
当x≥0时,y3=120.
这个问题看起来还是有点复杂,难点在于每一个函数的解析式都是分类表示的,需要分类讨论,而怎样分类是难点,怎么办?
综上分析我们把这个问题描述为函数问题,设上网时间为 X,方案A,B,C的上网费用分别为y1 元,y2 元, y3 元,且
——先画出图象看看.
方式A.
在同一坐标系画出它们的图象:
新 知 探 究
方式B.
方式C.
当x≥0时,y3=120.
7.当上网时__________时,选择方式A最省钱.
在同一坐标系画出它们的图象:
新 知 探 究
此时,A和B方式一样省钱
7.当上网时__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
在同一坐标系画出它们的图象:
新 知 探 究
此时,B和C方式一样省钱
7.当上网时__________时,选择方式A最省钱.
当上网时间__________时,选择方式B最省钱.
当上网时间_________时,选择方式C最省钱.
在同一坐标系画出它们的图象:
新 知 探 究
实际问题
一次函数问题
设变量
找对应关系
一次函数问题的解
实际问题的解
解释实
际意义
这个实际问题的解决过程中是怎样思考的?
解 后 反 思
某移动公司对于移动话费推出两种收费方式:
A方案:每月收取基本月租费15元,另收通话费为0.2元/分;
B方案: 零月租费,通话费为0.3元/分.
(1)试写出A,B两种方案所付话费y(元)与通话 时间t(分)之间的函数关系式;
(2)在同一坐标系画出这两个函数的图象,并指出哪种付费方式合算?
练 习 巩 固
A方案: y1 = 15+0.2t(t≥0)
B方案:y2 = 0.3t(t≥0).
解:(1) A方案: y1 = 15+0.2t(t≥0),
B方案:
y2 = 0.3t(t≥0).
(2)这两个函数的图象如下:
t(分)
O
50
150
100
10
20
y(元)
50
30
40
●
●
y1 = 15+0.2t
y2 = 0.3t
●
观察图象,可知:
当通话时间为150分时,选择A或B方案费用一样;
当通话时间少于150分时,选择B方案费合算;
当通话时间多于150分时,选择A方案合算.
练 习 巩 固
解决方案问题步骤:
1.把实际问题转化为数学函数问题,列出函数关系式(建立数学模型).
2.通过解不等式或画函数图象的方式确定自变量的范围.
3.利用一次函数的增减性知识从而选择出最佳方案.
课 堂 小 结
1.如图是甲、乙两家商店销售同一种产品的销售价 y(元)与销售量 x(件)之间的函数图象.下列说法, 其中正确的说法有 .(填序号)
①售2件时甲、乙两家售价一样;
②买1件时买乙家的合算;
③买3件时买甲家的合算;
④买1件时,售价约为3元.
课 后 作 业
2. 东风商场文具部的某种毛笔每支售价25元,书法练习本每本售价5元.该商场为了促销制定了两种优惠方案供顾客选择.
甲:买一支毛笔赠送一本书法练习本.
乙:按购买金额打九折付款.
某校欲为校书法兴趣组购买这种毛笔10支,书法练习本x(x≤10)本.如何选择方案购买呢?
课 后 作 业
