人教版五年级数学下册 质数和合数、奇数偶数的运算顺序 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版五年级数学下册 质数和合数、奇数偶数的运算顺序 同步拓展讲与练+奥数培优(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 69.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 00:00:00 | ||
图片预览


文档简介
质数和合数、奇数偶数的运算顺序
知识引入:
奇数和偶数
例题1:填空。
(1)质数的因数只有( )个,合数的因数至少有( )个。自然数中,最小的质数是( ),最小的合数是( )。
(2)自然数中,既是质数又是偶数的数是( ),既是奇数又是合数的最小数是( )。
(3)两个连续的自然数都是质数,这两个数是( )和 ( );两个连续的一位自然数都是合数,这两个数是( )和( )。
例题2:判断。
(1)所有的偶数都是合数。( )
(2)所有的奇数都是质数。( )
(3)自然数除了质数就是合数。( )
(4)三个连续的自然数中至少有一个是合数。( )
(5)2是所有合数的因数。( )
(6)因为6=2×3, 所以 6的倍数一定可以被2、3、6整除。( )
例题3:猜数游戏。
(1)我是20以内最大的质数。 ( )
(2)我是最小的两位质数。 ( )
(3)我是最小的两位合数。 ( )
知识精讲1:
1.质数的意义: 一个数,如果只有1和它本身两个因数,那么这样的数叫做质数(或素数)。
如2,3,5,7都是质数。
2.一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。如4,6,15,49都是合数。
3.最小的质数是2; 最小的合数是4; 1不是质数,也不是合数。
4.100以内质数表:
2 3 5 7 11
13 17 19 23 29
31 37 41 43 27
53 59 61 67 71
73 79 83 89 97
二、奇数偶数的运算顺序
例题4:填空。在( )里填上“奇数”或“偶数”。
(1)一个奇数加5的和是( )。
(2)一个偶数加8的和是( )。
(3)最小的两位数与最大的两位数的和是( )。
(4)相邻两个自然数的和是( ),相邻两个自然数的积是( )。
(5)两个数的和是18,这两个数可能都是( )数,也可能都是( )。
(6)两个数的积是24,这两个数可能都是( )数,也可能一个是( )数,另一个是( )数。
(7)任何一个奇数减1后,都是( )数。
(8)两个质数的和是12,这两个数分别是( )和( );两个质数的积是91,这两个质数分别是( )和( )。
(9)最小的一位质数与最小的两位质数的积是( )。
(10)1~20中,不是奇数的质数有( ),不是偶数的合数有( )。
(11)两个质数的积是21,这两个质数的和是( )。
(12)两个连续自然数都是质数,这两个数是( )和( )。两个连续自然数都是合数,它们最小是( )和( )。
例题5:不计算,判断下面算式的结果是奇数还是偶数。
368+796 11367-231 46397+2016 368×796 11367×231 46397×2016
( ) ( ) ( ) ( ) ( ) ( )
知识精讲2:奇数偶数的运算顺序
(1)和差的奇偶性:
奇数±偶数= ;奇数±奇数= ; 偶数±偶数= 。
(2)积的奇偶性:
奇数×奇数= ;奇数×偶数= ; 偶数×偶数= 。
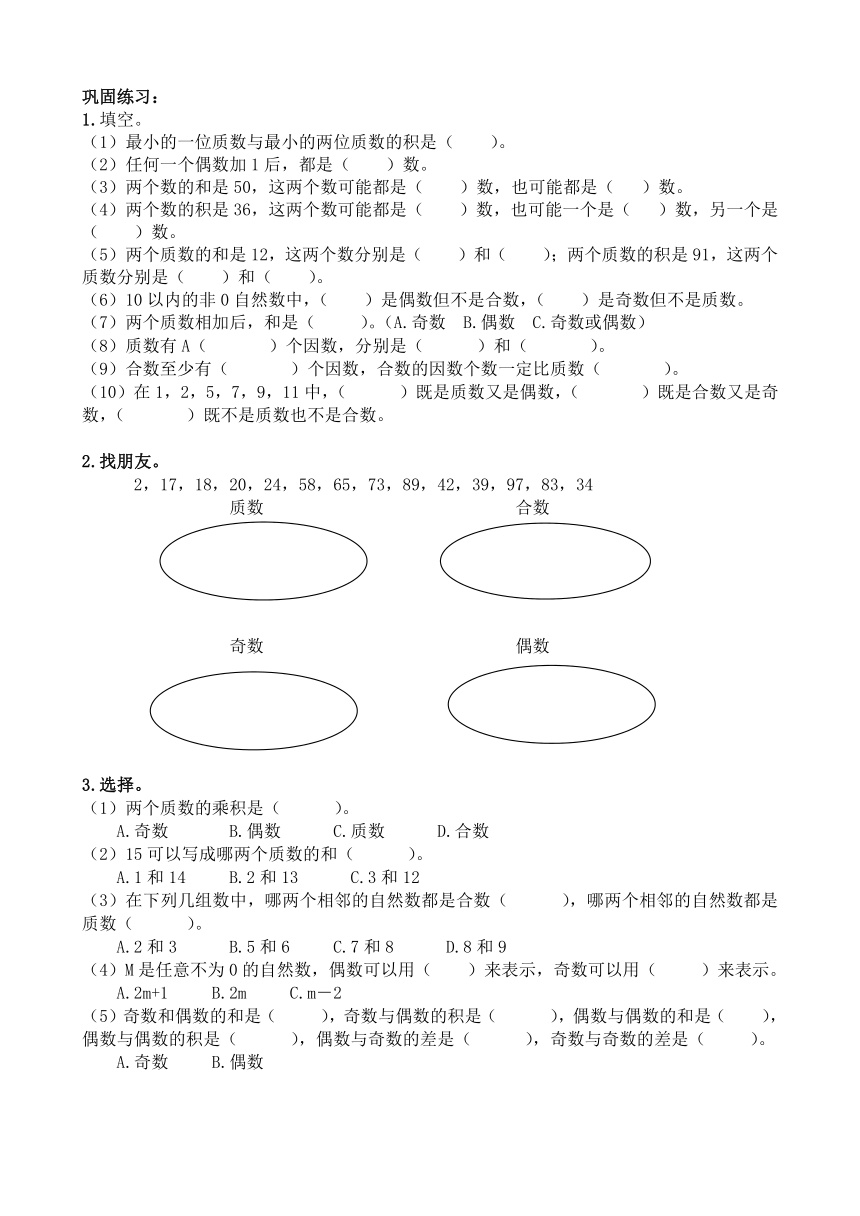
巩固练习:
1.填空。
最小的一位质数与最小的两位质数的积是( )。
任何一个偶数加1后,都是( )数。
两个数的和是50,这两个数可能都是( )数,也可能都是( )数。
两个数的积是36,这两个数可能都是( )数,也可能一个是( )数,另一个是( )数。
两个质数的和是12,这两个数分别是( )和( );两个质数的积是91,这两个质数分别是( )和( )。
10以内的非0自然数中,( )是偶数但不是合数,( )是奇数但不是质数。
两个质数相加后,和是( )。(A.奇数 B.偶数 C.奇数或偶数)
(8)质数有A( )个因数,分别是( )和( )。
(9)合数至少有( )个因数,合数的因数个数一定比质数( )。
(10)在1,2,5,7,9,11中,( )既是质数又是偶数,( )既是合数又是奇数,( )既不是质数也不是合数。
2.找朋友。
2,17,18,20,24,58,65,73,89,42,39,97,83,34
质数 合数
奇数 偶数
3.选择。
两个质数的乘积是( )。
A.奇数 B.偶数 C.质数 D.合数
(2)15可以写成哪两个质数的和( )。
A.1和14 B.2和13 C.3和12
(3)在下列几组数中,哪两个相邻的自然数都是合数( ),哪两个相邻的自然数都是质数( )。
A.2和3 B.5和6 C.7和8 D.8和9
(4)M是任意不为0的自然数,偶数可以用( )来表示,奇数可以用( )来表示。
A.2m+1 B.2m C.m-2
(5)奇数和偶数的和是( ),奇数与偶数的积是( ),偶数与偶数的和是( ),偶数与偶数的积是( ),偶数与奇数的差是( ),奇数与奇数的差是( )。
A.奇数 B.偶数
4.列式计算。
一个质数与它本身的10倍的和是55,这个质数是多少?
100以内最大的质数与最小的质数的积比它们的和是多多少?
有两个质数的和是18,积是65,这两个质数分别是多少?
1~20中,所有质数的和与合数的和相差多少?
(5)它是一个小于45的两位数,又是一个质数,且其数字之和是7,数字之差是1。这个数是多少?
(6)一个长方形的长和宽都是质数,并且周长是36cm,这个长方形的面积最大是多少平方厘米?
(7)两个质数的和是36,求这两个质数的积的最小值是多少?最大值是多少。
(8)两个质数的和是33,这这两个质数的积是多少?
(9)两个质数的积是33,这两个质数的和是多少?
5.推理解决实际问题。
(1)有126个苹果,把它们放在7个盘子里,每个盘子里只放奇数个苹果,能做到吗?
总结:奇数个奇数的和是 ,偶数个奇数的和是 。
奇数个偶数的和是 ,偶数个偶数的和是 。
(2)有2016个烟花,每次燃放奇数个,想在9次后恰好全部燃放,能做到吗?为什么?
(3) 1×2+3×4+5×6+…+199×200的和是奇数还是偶数?
(4)1+2+3+4+5+6+…+2007的和是奇数还是偶数?
奥数思维拓展:
运用列举法解决质数问题
1.渗透两种数学思想:化归思想、推理思想。
2.学习三类思维方法:推理法、列举法、图示法。
思维提升:
[例题1]三个不同质数的和是62,这三个质数的积最大是多少?
[分析]
除2以外所有的质数都是奇数。三个质数相加的和是偶数,必定有一个质数是2。62-2=60,另外两个质数的和是60,另外的两个质数可能的情况如下:
第一个质数 第二个质数 第三个质数 三个质数的积
7 53 742
13 47 1222
2 17 43 1462
19 41 1558
23 37 1702
29 31 1798
通过比较发现,当这两个质数是29和31时,这三个质数的积最大。
[解答]
2×29×31=1798
答:这三个质数的积最大是1798。
[技巧]
1.奇数个不同的质数相加,如果没有偶数2,和一定是奇数;如果和是偶数,其中一个质数一定是2。
2.两个数的和一定时,两个数的差越小,积就越大。
[例题2]三个不同质数的积是385,这三个不同质数的和是多少?
[分析]
因为385能被5整除,所以这三个指数中,必定有一个质数是5,385÷5=77,而77能被7整除,也一定有7,77÷7=11,所以这三个质数分别是5,7,11,它们的和是5+7+11=23。
[解答]
这三个不同质数的和是23。
[技巧]
解决这一类问题时,可以先找到这个数因数中的质数,再确定其它的质数。
举一反三:
1.三个不同质数的和是82,这三个质数的积最大是多少?
2.三个不同质数的积是1001,这三个质数的和是多少?
知识引入:
奇数和偶数
例题1:填空。
(1)质数的因数只有( )个,合数的因数至少有( )个。自然数中,最小的质数是( ),最小的合数是( )。
(2)自然数中,既是质数又是偶数的数是( ),既是奇数又是合数的最小数是( )。
(3)两个连续的自然数都是质数,这两个数是( )和 ( );两个连续的一位自然数都是合数,这两个数是( )和( )。
例题2:判断。
(1)所有的偶数都是合数。( )
(2)所有的奇数都是质数。( )
(3)自然数除了质数就是合数。( )
(4)三个连续的自然数中至少有一个是合数。( )
(5)2是所有合数的因数。( )
(6)因为6=2×3, 所以 6的倍数一定可以被2、3、6整除。( )
例题3:猜数游戏。
(1)我是20以内最大的质数。 ( )
(2)我是最小的两位质数。 ( )
(3)我是最小的两位合数。 ( )
知识精讲1:
1.质数的意义: 一个数,如果只有1和它本身两个因数,那么这样的数叫做质数(或素数)。
如2,3,5,7都是质数。
2.一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。如4,6,15,49都是合数。
3.最小的质数是2; 最小的合数是4; 1不是质数,也不是合数。
4.100以内质数表:
2 3 5 7 11
13 17 19 23 29
31 37 41 43 27
53 59 61 67 71
73 79 83 89 97
二、奇数偶数的运算顺序
例题4:填空。在( )里填上“奇数”或“偶数”。
(1)一个奇数加5的和是( )。
(2)一个偶数加8的和是( )。
(3)最小的两位数与最大的两位数的和是( )。
(4)相邻两个自然数的和是( ),相邻两个自然数的积是( )。
(5)两个数的和是18,这两个数可能都是( )数,也可能都是( )。
(6)两个数的积是24,这两个数可能都是( )数,也可能一个是( )数,另一个是( )数。
(7)任何一个奇数减1后,都是( )数。
(8)两个质数的和是12,这两个数分别是( )和( );两个质数的积是91,这两个质数分别是( )和( )。
(9)最小的一位质数与最小的两位质数的积是( )。
(10)1~20中,不是奇数的质数有( ),不是偶数的合数有( )。
(11)两个质数的积是21,这两个质数的和是( )。
(12)两个连续自然数都是质数,这两个数是( )和( )。两个连续自然数都是合数,它们最小是( )和( )。
例题5:不计算,判断下面算式的结果是奇数还是偶数。
368+796 11367-231 46397+2016 368×796 11367×231 46397×2016
( ) ( ) ( ) ( ) ( ) ( )
知识精讲2:奇数偶数的运算顺序
(1)和差的奇偶性:
奇数±偶数= ;奇数±奇数= ; 偶数±偶数= 。
(2)积的奇偶性:
奇数×奇数= ;奇数×偶数= ; 偶数×偶数= 。
巩固练习:
1.填空。
最小的一位质数与最小的两位质数的积是( )。
任何一个偶数加1后,都是( )数。
两个数的和是50,这两个数可能都是( )数,也可能都是( )数。
两个数的积是36,这两个数可能都是( )数,也可能一个是( )数,另一个是( )数。
两个质数的和是12,这两个数分别是( )和( );两个质数的积是91,这两个质数分别是( )和( )。
10以内的非0自然数中,( )是偶数但不是合数,( )是奇数但不是质数。
两个质数相加后,和是( )。(A.奇数 B.偶数 C.奇数或偶数)
(8)质数有A( )个因数,分别是( )和( )。
(9)合数至少有( )个因数,合数的因数个数一定比质数( )。
(10)在1,2,5,7,9,11中,( )既是质数又是偶数,( )既是合数又是奇数,( )既不是质数也不是合数。
2.找朋友。
2,17,18,20,24,58,65,73,89,42,39,97,83,34
质数 合数
奇数 偶数
3.选择。
两个质数的乘积是( )。
A.奇数 B.偶数 C.质数 D.合数
(2)15可以写成哪两个质数的和( )。
A.1和14 B.2和13 C.3和12
(3)在下列几组数中,哪两个相邻的自然数都是合数( ),哪两个相邻的自然数都是质数( )。
A.2和3 B.5和6 C.7和8 D.8和9
(4)M是任意不为0的自然数,偶数可以用( )来表示,奇数可以用( )来表示。
A.2m+1 B.2m C.m-2
(5)奇数和偶数的和是( ),奇数与偶数的积是( ),偶数与偶数的和是( ),偶数与偶数的积是( ),偶数与奇数的差是( ),奇数与奇数的差是( )。
A.奇数 B.偶数
4.列式计算。
一个质数与它本身的10倍的和是55,这个质数是多少?
100以内最大的质数与最小的质数的积比它们的和是多多少?
有两个质数的和是18,积是65,这两个质数分别是多少?
1~20中,所有质数的和与合数的和相差多少?
(5)它是一个小于45的两位数,又是一个质数,且其数字之和是7,数字之差是1。这个数是多少?
(6)一个长方形的长和宽都是质数,并且周长是36cm,这个长方形的面积最大是多少平方厘米?
(7)两个质数的和是36,求这两个质数的积的最小值是多少?最大值是多少。
(8)两个质数的和是33,这这两个质数的积是多少?
(9)两个质数的积是33,这两个质数的和是多少?
5.推理解决实际问题。
(1)有126个苹果,把它们放在7个盘子里,每个盘子里只放奇数个苹果,能做到吗?
总结:奇数个奇数的和是 ,偶数个奇数的和是 。
奇数个偶数的和是 ,偶数个偶数的和是 。
(2)有2016个烟花,每次燃放奇数个,想在9次后恰好全部燃放,能做到吗?为什么?
(3) 1×2+3×4+5×6+…+199×200的和是奇数还是偶数?
(4)1+2+3+4+5+6+…+2007的和是奇数还是偶数?
奥数思维拓展:
运用列举法解决质数问题
1.渗透两种数学思想:化归思想、推理思想。
2.学习三类思维方法:推理法、列举法、图示法。
思维提升:
[例题1]三个不同质数的和是62,这三个质数的积最大是多少?
[分析]
除2以外所有的质数都是奇数。三个质数相加的和是偶数,必定有一个质数是2。62-2=60,另外两个质数的和是60,另外的两个质数可能的情况如下:
第一个质数 第二个质数 第三个质数 三个质数的积
7 53 742
13 47 1222
2 17 43 1462
19 41 1558
23 37 1702
29 31 1798
通过比较发现,当这两个质数是29和31时,这三个质数的积最大。
[解答]
2×29×31=1798
答:这三个质数的积最大是1798。
[技巧]
1.奇数个不同的质数相加,如果没有偶数2,和一定是奇数;如果和是偶数,其中一个质数一定是2。
2.两个数的和一定时,两个数的差越小,积就越大。
[例题2]三个不同质数的积是385,这三个不同质数的和是多少?
[分析]
因为385能被5整除,所以这三个指数中,必定有一个质数是5,385÷5=77,而77能被7整除,也一定有7,77÷7=11,所以这三个质数分别是5,7,11,它们的和是5+7+11=23。
[解答]
这三个不同质数的和是23。
[技巧]
解决这一类问题时,可以先找到这个数因数中的质数,再确定其它的质数。
举一反三:
1.三个不同质数的和是82,这三个质数的积最大是多少?
2.三个不同质数的积是1001,这三个质数的和是多少?
