人教版五年级数学下册 分数和小数的互化 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版五年级数学下册 分数和小数的互化 同步拓展讲与练+奥数培优(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 302.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-12 17:43:55 | ||
图片预览




文档简介
分数和小数的互化
知识引入:
一、小数化成分数的方法
根据小数的意义,有限小数可以直接化成分母是10、100、1000、…的分数,原来是几位小数,就在1后面写几个零作分母,把原来的小数点去掉作分子。能约分的要约分。
如 :0.3 = , 0.02= = 。
例题1:把下列小数化成分数。
0.3=( ); 0.75=( ); 0.025=( ); 1.45=( );
二、分数化成小数的方法
(1)分母是10、100、1000、…的分数化成小数,可以直接去掉分母,看分母中1后面有几个零,就在分子中从最后一位起向左数出几位(位数不够用时用0补足),点上小数点。
如: = 0.1 , = 0.07 。
(2)分母不是10、100、1000、…的分数化成小数,用分子除以分母,除不尽时,根据需要按“四舍五入”法保留几位小数。
如: = 1 ÷ 2 = 0.5 , = 7 ÷ 2 = 3.5 。
例题2:把下列分数化成小数。
=( );=( );=( );=( );1=( );
三、如何判断一个最简分数是否可以化成有限小数
如果分母中除了2和5以外,不含有其他质因数,这个分数就能化成有限小数;
如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数。
如: 的分母20=2×2×2,所以 可以化成有限小数;
的分母15=3×5,可以 不能化成有限小数。
例题3:下列哪些分数能化成有限小数:
巩固练习:
1.填空。
小数化成分数时,有几位小数就要在1右面写( )作分母,原来的小数去掉( )作分子。
把小数化成分数时,要注意 。
在一列数中,既有分数,又有小数。在比较大小时有两种方法:一是 ,二是 ,再比较大小。
用分数表示为( ),化成小数为( )。
用分数表示为( ),化成小数为( )。
(6)一位小数表示( ),两位小数表示( ),三位小数表示( )。
(7)0.04里有( )个百分之一,写成分数是( )。
(8)0.375里有( )个千分之一,写成分数是( )。
(9)0.3里有( )个0.01,有( )个百分之一。
2.判断。
=3.7( )
1.035=( )
3.05=( )
3.找朋友。
0.6 0.24 0.8
1.025 0.35
在 里填上“>”“<”或“=”。
0.375 1.018 0.67
0.912 3.16 0.77
0.184 2.5 0.02
3.74 0.12 0.02
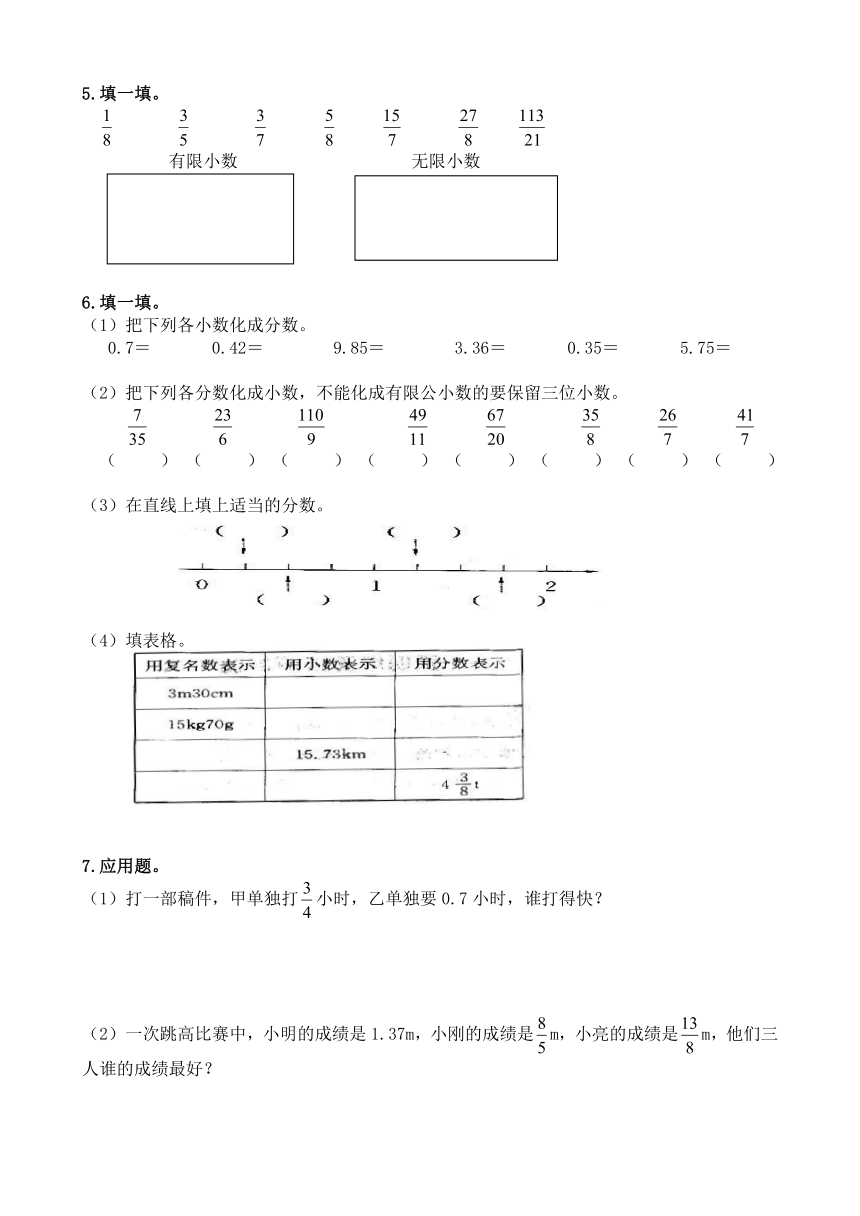
5.填一填。
有限小数 无限小数
6.填一填。
把下列各小数化成分数。
0.7= 0.42= 9.85= 3.36= 0.35= 5.75=
把下列各分数化成小数,不能化成有限公小数的要保留三位小数。
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
在直线上填上适当的分数。
(4)填表格。
7.应用题。
打一部稿件,甲单独打小时,乙单独要0.7小时,谁打得快?
一次跳高比赛中,小明的成绩是1.37m,小刚的成绩是m,小亮的成绩是m,他们三人谁的成绩最好?
兰兰的身高为1.53m,丽丽的身高为159cm,芳芳的身高为m,谁最高,谁最矮?
(4)甲、乙、丙三位工人师傅加工一批零件,甲每小时加工32个,乙15分钟加工13个,丙6分钟加工5个,谁加工得快?
分数的意义和性质单元小结:
1.填空。
(1)在下面的括号里填上适当的分数。
40平方分米=( )平方米 75厘米=( )米 350千克=( )吨
(2)表示( ),
还可以表示( )。
(3)的分数单位是( ),它有( )个这样的分数单位。
(4)在下面的○里填上“>”、“<”或“=”符号。
○0.125 ○1 4○3 6.5千米○6千米
(5)在下面的括号里填上适当的数。
是( )个 0.875===
(6)3米长的铁丝平均分成8段,每段长米,用小数表示是( )米。
(7)8和9的最大公因数是( ),最小公倍数是( )。
12和72的最大公因数是( ),最小公倍数是( )。
(8)一个数3、5、7分别除都余1,这个数最小是( )。
(9)一项工程必须在30天完成,平均每天完成全部工程的。7天完成这项工程的。19天完成这项工程的。
(10)两个数的最小公倍数是180,最大公因数是30,其中一个数是90,另一个数是( )。
(11)一个最简分数,如果能化成有限小数,它的分母中只含有质因数( )。
(12)a和b是互质数,它们的最大公因数是( ),最小公倍数是( )。
(13)在下面的括号里填上适当的分数。
(14)用直线上的点表示下面各数。
1 2 3
2.选择题。将正确答案的序号填在题中的括号里。
(1)米表示的意义是把( )平均分成7份,表示其中的4份。
①4米 ②1米 ③单位1
(2)一个分数,分子不变,分母扩大4倍,这个分数值就( )
①不变 ②扩大4倍 ③缩小4倍
(3)甲每小时做7个零件,乙每小时做8个零件,做一个零件( )
①甲用的时间多 ②乙用的时间多 ③两人用的时间同样多。
(4)把一个分数约分,用分子和分母的( )去约,比较简便。
①公约数 ②最小公倍数 ③最大公因数
(5)12是36和24的( )
①最小公倍数 ②最大公因数 ③公倍数
(6)两个自然数相除,不能整除的时候,它们的商可以用( )来表示。
①分数 ②循环节 ③余数
3.把下面的假分数化成带分数或整数。
4.把下面的分数约分,是假分数的要化成带分数或整数。
1
把下面各组分数通分。
和 和 、和
、和 1、4和7 1、3和2
分数和小数的互化。
把下面的小数化成分数。
0.8 1.7 3.4 4.875 24.125
(2)下面的分数化成小数,(除不尽的保留两位小数)。
2 3
(3)把0.29 , , 0.3 , , 按从小到大的顺序排列。
7.解决问题。
(1)五、一班有男生20人,比女生少5人,男、女生人数各占全班人数的几分之几?
(2)五、二班上学期体育达标的有52人,其中男生有28人,男、女生达标人数各占达标总人数的几分之几?
(3)一本科技书,小磊看过50页,还剩下31页没有看,看过的和没有看过的各占这本书总页数的几分之几?
(4)张师傅6分钟做7个零件,王师傅7分钟做8个零件,他们两人每分钟各做多少个零件?谁做得快些?
(5)解放军进行军事训练,第一天4小时行了58千米,第二天5小时走了73千米,哪一天走得快些?
(6)学校植树,每行栽12棵、16棵或20棵三种栽法,都刚好排成整行而无剩余。问至少有多少棵树?
奥数思维拓展(一):解决分数问题
1.渗透两种数学思想:推理思想、化归思想。
2.学习两类思维方法:观察法、分析法。
思维提升:
[例] 化成小数后,小数点后第1位到2003位的数字之和是多少?
[分析]
化成小数是个循环小数,看小数部分每几位一个循环,看每组循环数字的和是多少,然后再乘组数加上余下数字之和。
[解答]
=0.857142,循环数字有6位,2003÷6=333……5,2003个数中共有333组零5个数,每组的和是8+5+7+1+4+2=27,所以27×333+8+5+7+1+4=9016。
[技巧]
求一个分数化成循环小数后一些连续小数位上的数字的和,先找出每组循环的数字求出和,再看要求的位数里面有多少组,用组数×每组的数字之和,如果有剩余,就加上余下的几个数字。
举一反三:
1. 化成小数后,小数点后第1位到192位的数字之和是多少?
2. 化成小数后,小数点后第1位到314位的数字之和是多少?
3. 化成小数后,小数点后第1位到1045位的数字之和是多少?
奥数思维拓展(二):循环小数化成分数
1.渗透两种数学思想:推理思想、化归思想。
2.学习两类思维方法:观察法、分析法。
思维提升:
[例]把0.53和0.231化成分数。
[分析与解答]
(1)0.53是纯循环小数,可以用移动循环节的方法化循环小数为分数。
0.53=0.53①
0.53×100=53.53②
②-①得:0.53×100-0.53=53.53-0.53
0.53×(100-1)=53
0.53=
(2)0.231是混循环小数,同样也可以采用上面的方法。
0.231×10=2.31③
0.231×1000=231.31④
④-③得:0.231×1000-0.231×10=231.31-2.31
0.231×(1000-10)=231.31-2.31
0.231×990=229
0.231=
[技巧]
1.纯循环小数化成分数:分子是由一个循环节的数字组成的,分母的个位数字都是9,9的个数与循环节的位数相同。字母表示为:0.ab= 。
2.混循环小数化成分数:分子是小数点后面第一个数字至第一个循环节的末尾数字所组成的数,减去不循数字所组成的数得的差;分母的头几位数字是9,末位数字是0,9的个数和循环节的位数相同,0的个数和不循环部分的位数相同。字母表示为:0.abc= 。
举一反三:
把0.47和0.156化成分数。
“1”
( )
“1”
( )
知识引入:
一、小数化成分数的方法
根据小数的意义,有限小数可以直接化成分母是10、100、1000、…的分数,原来是几位小数,就在1后面写几个零作分母,把原来的小数点去掉作分子。能约分的要约分。
如 :0.3 = , 0.02= = 。
例题1:把下列小数化成分数。
0.3=( ); 0.75=( ); 0.025=( ); 1.45=( );
二、分数化成小数的方法
(1)分母是10、100、1000、…的分数化成小数,可以直接去掉分母,看分母中1后面有几个零,就在分子中从最后一位起向左数出几位(位数不够用时用0补足),点上小数点。
如: = 0.1 , = 0.07 。
(2)分母不是10、100、1000、…的分数化成小数,用分子除以分母,除不尽时,根据需要按“四舍五入”法保留几位小数。
如: = 1 ÷ 2 = 0.5 , = 7 ÷ 2 = 3.5 。
例题2:把下列分数化成小数。
=( );=( );=( );=( );1=( );
三、如何判断一个最简分数是否可以化成有限小数
如果分母中除了2和5以外,不含有其他质因数,这个分数就能化成有限小数;
如果分母中含有2和5以外的质因数,这个分数就不能化成有限小数。
如: 的分母20=2×2×2,所以 可以化成有限小数;
的分母15=3×5,可以 不能化成有限小数。
例题3:下列哪些分数能化成有限小数:
巩固练习:
1.填空。
小数化成分数时,有几位小数就要在1右面写( )作分母,原来的小数去掉( )作分子。
把小数化成分数时,要注意 。
在一列数中,既有分数,又有小数。在比较大小时有两种方法:一是 ,二是 ,再比较大小。
用分数表示为( ),化成小数为( )。
用分数表示为( ),化成小数为( )。
(6)一位小数表示( ),两位小数表示( ),三位小数表示( )。
(7)0.04里有( )个百分之一,写成分数是( )。
(8)0.375里有( )个千分之一,写成分数是( )。
(9)0.3里有( )个0.01,有( )个百分之一。
2.判断。
=3.7( )
1.035=( )
3.05=( )
3.找朋友。
0.6 0.24 0.8
1.025 0.35
在 里填上“>”“<”或“=”。
0.375 1.018 0.67
0.912 3.16 0.77
0.184 2.5 0.02
3.74 0.12 0.02
5.填一填。
有限小数 无限小数
6.填一填。
把下列各小数化成分数。
0.7= 0.42= 9.85= 3.36= 0.35= 5.75=
把下列各分数化成小数,不能化成有限公小数的要保留三位小数。
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
在直线上填上适当的分数。
(4)填表格。
7.应用题。
打一部稿件,甲单独打小时,乙单独要0.7小时,谁打得快?
一次跳高比赛中,小明的成绩是1.37m,小刚的成绩是m,小亮的成绩是m,他们三人谁的成绩最好?
兰兰的身高为1.53m,丽丽的身高为159cm,芳芳的身高为m,谁最高,谁最矮?
(4)甲、乙、丙三位工人师傅加工一批零件,甲每小时加工32个,乙15分钟加工13个,丙6分钟加工5个,谁加工得快?
分数的意义和性质单元小结:
1.填空。
(1)在下面的括号里填上适当的分数。
40平方分米=( )平方米 75厘米=( )米 350千克=( )吨
(2)表示( ),
还可以表示( )。
(3)的分数单位是( ),它有( )个这样的分数单位。
(4)在下面的○里填上“>”、“<”或“=”符号。
○0.125 ○1 4○3 6.5千米○6千米
(5)在下面的括号里填上适当的数。
是( )个 0.875===
(6)3米长的铁丝平均分成8段,每段长米,用小数表示是( )米。
(7)8和9的最大公因数是( ),最小公倍数是( )。
12和72的最大公因数是( ),最小公倍数是( )。
(8)一个数3、5、7分别除都余1,这个数最小是( )。
(9)一项工程必须在30天完成,平均每天完成全部工程的。7天完成这项工程的。19天完成这项工程的。
(10)两个数的最小公倍数是180,最大公因数是30,其中一个数是90,另一个数是( )。
(11)一个最简分数,如果能化成有限小数,它的分母中只含有质因数( )。
(12)a和b是互质数,它们的最大公因数是( ),最小公倍数是( )。
(13)在下面的括号里填上适当的分数。
(14)用直线上的点表示下面各数。
1 2 3
2.选择题。将正确答案的序号填在题中的括号里。
(1)米表示的意义是把( )平均分成7份,表示其中的4份。
①4米 ②1米 ③单位1
(2)一个分数,分子不变,分母扩大4倍,这个分数值就( )
①不变 ②扩大4倍 ③缩小4倍
(3)甲每小时做7个零件,乙每小时做8个零件,做一个零件( )
①甲用的时间多 ②乙用的时间多 ③两人用的时间同样多。
(4)把一个分数约分,用分子和分母的( )去约,比较简便。
①公约数 ②最小公倍数 ③最大公因数
(5)12是36和24的( )
①最小公倍数 ②最大公因数 ③公倍数
(6)两个自然数相除,不能整除的时候,它们的商可以用( )来表示。
①分数 ②循环节 ③余数
3.把下面的假分数化成带分数或整数。
4.把下面的分数约分,是假分数的要化成带分数或整数。
1
把下面各组分数通分。
和 和 、和
、和 1、4和7 1、3和2
分数和小数的互化。
把下面的小数化成分数。
0.8 1.7 3.4 4.875 24.125
(2)下面的分数化成小数,(除不尽的保留两位小数)。
2 3
(3)把0.29 , , 0.3 , , 按从小到大的顺序排列。
7.解决问题。
(1)五、一班有男生20人,比女生少5人,男、女生人数各占全班人数的几分之几?
(2)五、二班上学期体育达标的有52人,其中男生有28人,男、女生达标人数各占达标总人数的几分之几?
(3)一本科技书,小磊看过50页,还剩下31页没有看,看过的和没有看过的各占这本书总页数的几分之几?
(4)张师傅6分钟做7个零件,王师傅7分钟做8个零件,他们两人每分钟各做多少个零件?谁做得快些?
(5)解放军进行军事训练,第一天4小时行了58千米,第二天5小时走了73千米,哪一天走得快些?
(6)学校植树,每行栽12棵、16棵或20棵三种栽法,都刚好排成整行而无剩余。问至少有多少棵树?
奥数思维拓展(一):解决分数问题
1.渗透两种数学思想:推理思想、化归思想。
2.学习两类思维方法:观察法、分析法。
思维提升:
[例] 化成小数后,小数点后第1位到2003位的数字之和是多少?
[分析]
化成小数是个循环小数,看小数部分每几位一个循环,看每组循环数字的和是多少,然后再乘组数加上余下数字之和。
[解答]
=0.857142,循环数字有6位,2003÷6=333……5,2003个数中共有333组零5个数,每组的和是8+5+7+1+4+2=27,所以27×333+8+5+7+1+4=9016。
[技巧]
求一个分数化成循环小数后一些连续小数位上的数字的和,先找出每组循环的数字求出和,再看要求的位数里面有多少组,用组数×每组的数字之和,如果有剩余,就加上余下的几个数字。
举一反三:
1. 化成小数后,小数点后第1位到192位的数字之和是多少?
2. 化成小数后,小数点后第1位到314位的数字之和是多少?
3. 化成小数后,小数点后第1位到1045位的数字之和是多少?
奥数思维拓展(二):循环小数化成分数
1.渗透两种数学思想:推理思想、化归思想。
2.学习两类思维方法:观察法、分析法。
思维提升:
[例]把0.53和0.231化成分数。
[分析与解答]
(1)0.53是纯循环小数,可以用移动循环节的方法化循环小数为分数。
0.53=0.53①
0.53×100=53.53②
②-①得:0.53×100-0.53=53.53-0.53
0.53×(100-1)=53
0.53=
(2)0.231是混循环小数,同样也可以采用上面的方法。
0.231×10=2.31③
0.231×1000=231.31④
④-③得:0.231×1000-0.231×10=231.31-2.31
0.231×(1000-10)=231.31-2.31
0.231×990=229
0.231=
[技巧]
1.纯循环小数化成分数:分子是由一个循环节的数字组成的,分母的个位数字都是9,9的个数与循环节的位数相同。字母表示为:0.ab= 。
2.混循环小数化成分数:分子是小数点后面第一个数字至第一个循环节的末尾数字所组成的数,减去不循数字所组成的数得的差;分母的头几位数字是9,末位数字是0,9的个数和循环节的位数相同,0的个数和不循环部分的位数相同。字母表示为:0.abc= 。
举一反三:
把0.47和0.156化成分数。
“1”
( )
“1”
( )
