六年级下册数学课件 圆柱和圆锥整理与复习 北京版(39张ppt)
文档属性
| 名称 | 六年级下册数学课件 圆柱和圆锥整理与复习 北京版(39张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 06:44:01 | ||
图片预览



文档简介
(共39张PPT)
圆柱和圆锥整理与复习
六年级 数学
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
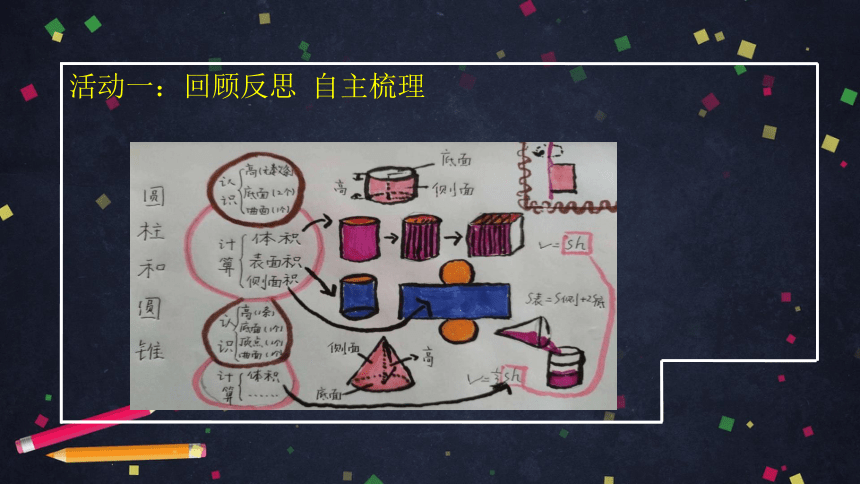
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
圆锥
圆柱
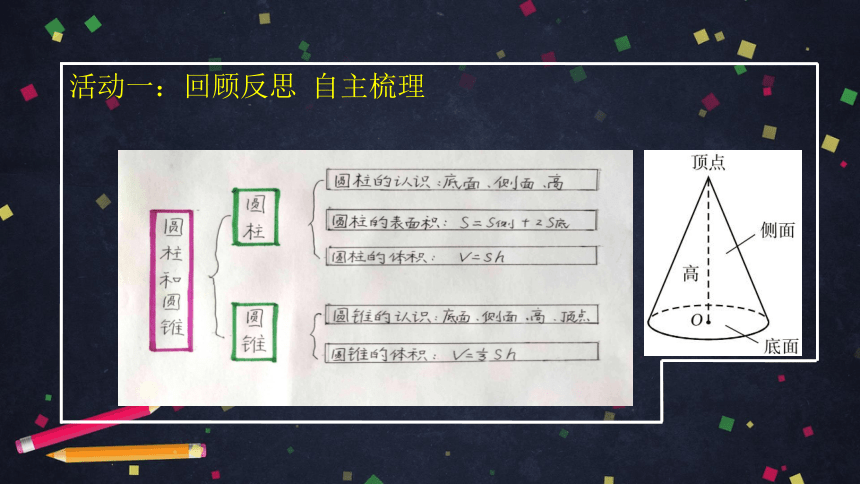
圆锥的认识
底面 侧面 高 顶点
实验
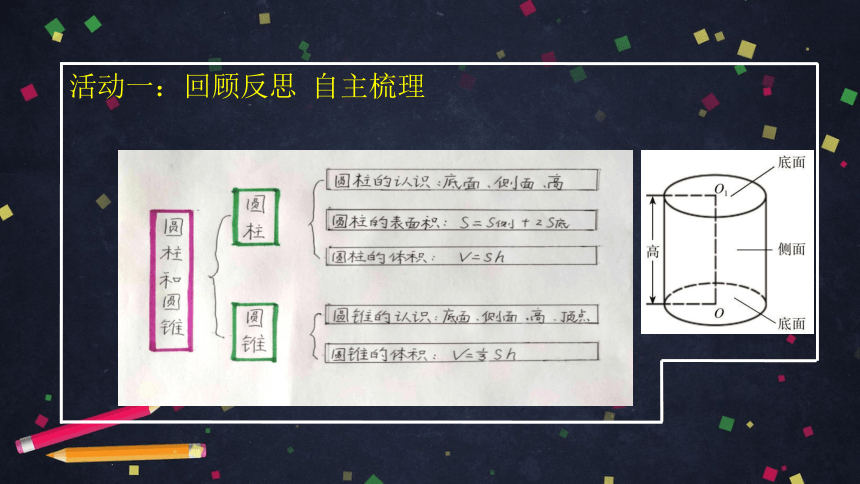
圆柱的体积
V=Sh
圆柱的认识
底面 侧面 高
圆柱的表面积
S表=S侧+2S底
观察 围合 旋转 平移 切截
由表及里
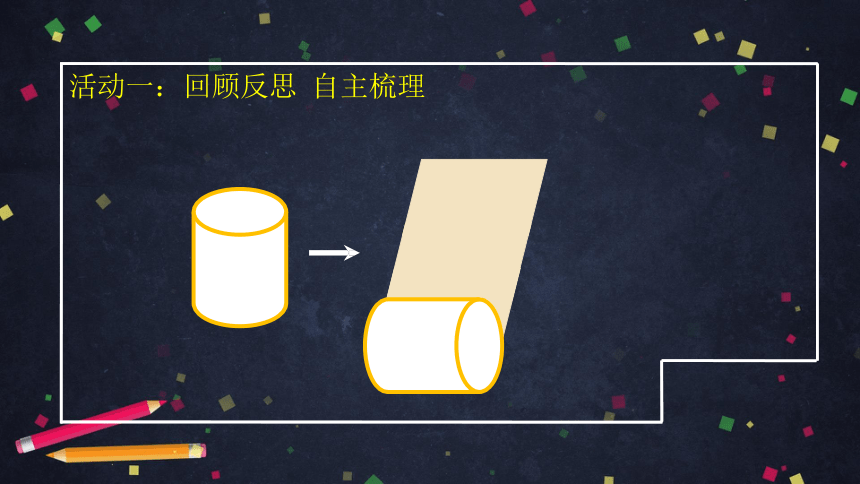
展开
立体到平面
体积不变 形状变化 猜想 验证
圆锥的体积
????
V= S h
15
厘
米
图①
?
活动二:从平面图形到立体图形
看到了图①,你能确定这个立体图形的形状吗?
10厘米
10厘米
图②
?
15
厘
米
图①
10厘米
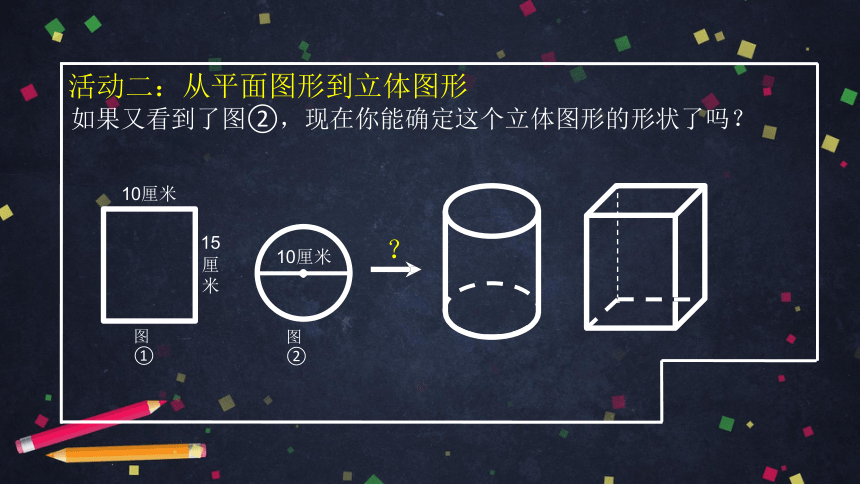
活动二:从平面图形到立体图形
如果又看到了图②,现在你能确定这个立体图形的形状了吗?
15
厘
米
图①
10厘米
10厘米
图②
活动二:从平面图形到立体图形
如果又看到了图②,现在你能确定这个立体图形的形状了吗?
15
厘 米
10厘米
10厘米
15
厘
米
图①
10厘米
图②
活动二:从平面图形到立体图形
如果又看到了图②,现在你能确定这个立体图形的形状了吗?
10厘米
15
厘
米
活动二:从平面图形到立体图形
如果这个长方形是圆柱的截面图,你能确定这个圆柱的形状吗?
10厘米
15
厘
米
活动二:从平面图形到立体图形
如果这个长方形是圆柱的截面图,你能确定这个圆柱的形状吗?
15
厘
米
10厘米
活动二:从平面图形到立体图形
如果这个截面通过两底面的圆心, 能确定这个圆柱的形状吗?
10厘米
15
厘
米
图③
?
10厘米
活动二:从平面图形到立体图形
图③是圆锥的截面图,根据图③你能确定圆锥的形状吗?
?
图③
10厘米
活动二:从平面图形到立体图形
图③是圆锥的截面图,根据图③你能确定圆锥的形状吗?
活动二:从平面图形到立体图形
15
厘 米
10厘米
15
厘 米
10厘米
16
厘
米
20厘米
20
厘 米
16厘米
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
底面周长/厘米 底面半径/厘米 高/厘米 体积/立方厘米
20 3.2 16 514.5
16 2.5 20 392.5
?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
为什么以长边为底面周长围成的圆
柱体积大呢?
底面周长/厘米 底面半径/厘米 高/厘米 体积/立方厘米
20 3.2 16 514.5
16 2.5 20 392.5
?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
为什么以长边为底面周长围成的圆
柱体积大呢?
图①
为什么以长边为底面周长围成的圆
柱体积大呢?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
图②
长方体的体积 = 底面积 × 高
圆柱的体积 = 侧面积的一半×半径
?
为什么以长边为底面周长围成的圆
柱体积大呢?
?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
底面周长/厘米 底面半径/厘米 高/厘米 体积/立方厘米
20 3.2 16 514.5
16 2.5 20 392.5
长方体的体积 = 底面积 × 高
圆柱的体积 = 侧面积的一半×半径
我买了一支底面积是0.3平方厘 米的铅笔。用了几天后……
这支铅笔的体积是多少立方厘米?
剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
活动四:综合应用 解决问题
我买了一支底面积是0.3平方厘 米的铅笔。用了几天后……
1.这支铅笔的体积是多少立方厘米?
0.3×18=5.4(立方厘米)
答:这支铅笔的体积是5.4立方厘米。
我买了一支底面积是0.3平方厘 米的铅笔。用了几天后……
这支铅笔的体积是多少立方厘米?
剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
活动四:综合应用 解决问题
2.剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
2.剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
2.剩余部分的体积是多少立方厘米?
12份
回顾反思
回顾反思 自主梳理
从平面图形到立体图形
围圆柱的小秘密
综合应用 解决问题
圆锥
圆柱
圆锥的认识
底面 侧面 高 顶点
体积不变 形状变化 猜想 验证
圆锥的表面积
实验
圆柱的体积
V=Sh
圆柱的认识
底面 侧面 高
圆柱的表面积
S表=S侧+2S底
圆锥的体积
????
V= S h
观察 围合 旋转 平移 切截
由表及里
展开
立体到平面
新形体
认识
表面积
体积
回顾反思
课后作业
1.数学书第19页第6题
课后作业
2.数学书第19页第7题
课后作业
3.数学书第20页第12题
课后作业
4.数学书第20页第13题
课后作业
5.选择一个生活中的物体,用自己喜欢的方法认识它。
再 见
圆柱和圆锥整理与复习
六年级 数学
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
活动一:回顾反思 自主梳理
圆锥
圆柱
圆锥的认识
底面 侧面 高 顶点
实验
圆柱的体积
V=Sh
圆柱的认识
底面 侧面 高
圆柱的表面积
S表=S侧+2S底
观察 围合 旋转 平移 切截
由表及里
展开
立体到平面
体积不变 形状变化 猜想 验证
圆锥的体积
????
V= S h
15
厘
米
图①
?
活动二:从平面图形到立体图形
看到了图①,你能确定这个立体图形的形状吗?
10厘米
10厘米
图②
?
15
厘
米
图①
10厘米
活动二:从平面图形到立体图形
如果又看到了图②,现在你能确定这个立体图形的形状了吗?
15
厘
米
图①
10厘米
10厘米
图②
活动二:从平面图形到立体图形
如果又看到了图②,现在你能确定这个立体图形的形状了吗?
15
厘 米
10厘米
10厘米
15
厘
米
图①
10厘米
图②
活动二:从平面图形到立体图形
如果又看到了图②,现在你能确定这个立体图形的形状了吗?
10厘米
15
厘
米
活动二:从平面图形到立体图形
如果这个长方形是圆柱的截面图,你能确定这个圆柱的形状吗?
10厘米
15
厘
米
活动二:从平面图形到立体图形
如果这个长方形是圆柱的截面图,你能确定这个圆柱的形状吗?
15
厘
米
10厘米
活动二:从平面图形到立体图形
如果这个截面通过两底面的圆心, 能确定这个圆柱的形状吗?
10厘米
15
厘
米
图③
?
10厘米
活动二:从平面图形到立体图形
图③是圆锥的截面图,根据图③你能确定圆锥的形状吗?
?
图③
10厘米
活动二:从平面图形到立体图形
图③是圆锥的截面图,根据图③你能确定圆锥的形状吗?
活动二:从平面图形到立体图形
15
厘 米
10厘米
15
厘 米
10厘米
16
厘
米
20厘米
20
厘 米
16厘米
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
底面周长/厘米 底面半径/厘米 高/厘米 体积/立方厘米
20 3.2 16 514.5
16 2.5 20 392.5
?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
为什么以长边为底面周长围成的圆
柱体积大呢?
底面周长/厘米 底面半径/厘米 高/厘米 体积/立方厘米
20 3.2 16 514.5
16 2.5 20 392.5
?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
为什么以长边为底面周长围成的圆
柱体积大呢?
图①
为什么以长边为底面周长围成的圆
柱体积大呢?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
图②
长方体的体积 = 底面积 × 高
圆柱的体积 = 侧面积的一半×半径
?
为什么以长边为底面周长围成的圆
柱体积大呢?
?
活动三:围圆柱的小秘密
用一张长方形纸围成圆柱的侧面,如果再配上两个底面,做成 一个圆柱。这个圆柱的体积是多少?
底面周长/厘米 底面半径/厘米 高/厘米 体积/立方厘米
20 3.2 16 514.5
16 2.5 20 392.5
长方体的体积 = 底面积 × 高
圆柱的体积 = 侧面积的一半×半径
我买了一支底面积是0.3平方厘 米的铅笔。用了几天后……
这支铅笔的体积是多少立方厘米?
剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
活动四:综合应用 解决问题
我买了一支底面积是0.3平方厘 米的铅笔。用了几天后……
1.这支铅笔的体积是多少立方厘米?
0.3×18=5.4(立方厘米)
答:这支铅笔的体积是5.4立方厘米。
我买了一支底面积是0.3平方厘 米的铅笔。用了几天后……
这支铅笔的体积是多少立方厘米?
剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
活动四:综合应用 解决问题
2.剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
2.剩余部分的体积是多少立方厘米?
活动四:综合应用 解决问题
2.剩余部分的体积是多少立方厘米?
12份
回顾反思
回顾反思 自主梳理
从平面图形到立体图形
围圆柱的小秘密
综合应用 解决问题
圆锥
圆柱
圆锥的认识
底面 侧面 高 顶点
体积不变 形状变化 猜想 验证
圆锥的表面积
实验
圆柱的体积
V=Sh
圆柱的认识
底面 侧面 高
圆柱的表面积
S表=S侧+2S底
圆锥的体积
????
V= S h
观察 围合 旋转 平移 切截
由表及里
展开
立体到平面
新形体
认识
表面积
体积
回顾反思
课后作业
1.数学书第19页第6题
课后作业
2.数学书第19页第7题
课后作业
3.数学书第20页第12题
课后作业
4.数学书第20页第13题
课后作业
5.选择一个生活中的物体,用自己喜欢的方法认识它。
再 见
