六年级下册数学课件 圆锥的体积(二) 北京版(32张ppt)
文档属性
| 名称 | 六年级下册数学课件 圆锥的体积(二) 北京版(32张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 06:44:52 | ||
图片预览











文档简介
(共32张PPT)
圆锥的体积(二)
六年级 数学
令-
?
...
.
II
□
/云雾,
--- - - - -
□
□
口
马 ·
“
口
笆
,
如果用圆柱形状的木材加工成一个最大 的圆锥,这个圆锥的体积是多少?削掉 部分的体积又是多少?
陀螺的体积是多少呢?
蒙古包所占空间的大小是多少? 蒙古包的形状可以通过什么样的图 形旋转而成呢?
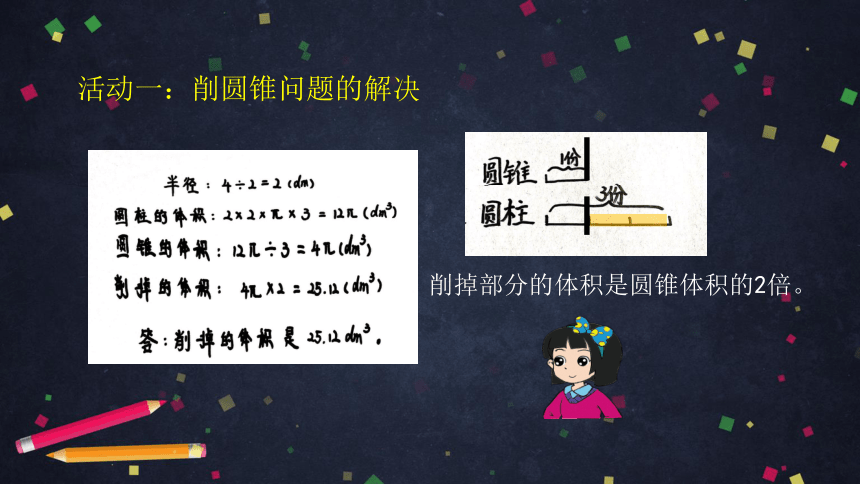
活动一:削圆锥问题的解决
如果用圆柱形状的木材加工成一个最大的圆锥,这个 圆锥的体积是多少?削掉部分的体积又是多少?
怎么削才会得到体积最大
的圆锥呢?
等底等高
活动一:削圆锥问题的解决
削掉部分的体积是圆锥体积的2倍。
活动一:削圆锥问题的解决
活动一:削圆锥问题的解决
半径:4÷2 = 2(dm)
圆柱的体积:2×2×π×3 = 37.68( dm?
1
圆锥的体积:37.68× 3 = 12.56(dm?
削掉部分的体积:37.68-12.56 = 25.12(dm?
活动二:陀螺问题的解决
3cm
陀螺的体积是多少?
3cm
6cm
活动二:陀螺问题的解决
6cm
3cm
3cm
陀螺体积: ×3×3×π×(3+3)= 56.52( cm? )
半径:6÷2 = 3(cm)
1
3
活动二:陀螺问题的解决
这个蒙古包所占的空间是多少立方米?
3m
2m
6m
活动三:蒙古包问题的解决
活动三:蒙古包问题的解决
3m
2m
6m
6
活动三:蒙古包问题的解决
1
1m
2m
6m
3m
2m
1m
想象
活动三:蒙古包问题的解决
蒙古包的形状可以通过什么样的图形旋转而成呢?
活动四:思考题
21
32
3
数学书第17页 思考题
一个直角梯形(如图,图中单位: 米),如果分别以 直角梯形的上底、下底所在的直线为轴旋转一周,那么 所形成的立体图形的体积哪个大?为什么?
活动四:思考题
①
②
活动四:思考题
①
②
活动四:思考题
②
①
①
1 份
2 份
2
3
3
2
3
3
-
活动四:思考题
圆柱的体积:3×3×π×3=27π( m? )
圆锥的体积:3×3×π×(3-2)× 1 =3π(m?)
3
差:27π-3π = 24π = 75.36(m?)75.36m?>65.94m?
课后作业
1.数学书第17页第5题
课后作业
2.数学书第19页第7题
课后作业
3.数学书第20页第10题
课后作业
4.观察生活,提出与圆柱圆锥有关的实际问 题,并尝试解答。
课前参与
回顾与梳理本单元学习的知识、方法,用自 己喜欢的方式表达。
再见
圆锥的体积(二)
六年级 数学
令-
?
...
.
II
□
/云雾,
--- - - - -
□
□
口
马 ·
“
口
笆
,
如果用圆柱形状的木材加工成一个最大 的圆锥,这个圆锥的体积是多少?削掉 部分的体积又是多少?
陀螺的体积是多少呢?
蒙古包所占空间的大小是多少? 蒙古包的形状可以通过什么样的图 形旋转而成呢?
活动一:削圆锥问题的解决
如果用圆柱形状的木材加工成一个最大的圆锥,这个 圆锥的体积是多少?削掉部分的体积又是多少?
怎么削才会得到体积最大
的圆锥呢?
等底等高
活动一:削圆锥问题的解决
削掉部分的体积是圆锥体积的2倍。
活动一:削圆锥问题的解决
活动一:削圆锥问题的解决
半径:4÷2 = 2(dm)
圆柱的体积:2×2×π×3 = 37.68( dm?
1
圆锥的体积:37.68× 3 = 12.56(dm?
削掉部分的体积:37.68-12.56 = 25.12(dm?
活动二:陀螺问题的解决
3cm
陀螺的体积是多少?
3cm
6cm
活动二:陀螺问题的解决
6cm
3cm
3cm
陀螺体积: ×3×3×π×(3+3)= 56.52( cm? )
半径:6÷2 = 3(cm)
1
3
活动二:陀螺问题的解决
这个蒙古包所占的空间是多少立方米?
3m
2m
6m
活动三:蒙古包问题的解决
活动三:蒙古包问题的解决
3m
2m
6m
6
活动三:蒙古包问题的解决
1
1m
2m
6m
3m
2m
1m
想象
活动三:蒙古包问题的解决
蒙古包的形状可以通过什么样的图形旋转而成呢?
活动四:思考题
21
32
3
数学书第17页 思考题
一个直角梯形(如图,图中单位: 米),如果分别以 直角梯形的上底、下底所在的直线为轴旋转一周,那么 所形成的立体图形的体积哪个大?为什么?
活动四:思考题
①
②
活动四:思考题
①
②
活动四:思考题
②
①
①
1 份
2 份
2
3
3
2
3
3
-
活动四:思考题
圆柱的体积:3×3×π×3=27π( m? )
圆锥的体积:3×3×π×(3-2)× 1 =3π(m?)
3
差:27π-3π = 24π = 75.36(m?)75.36m?>65.94m?
课后作业
1.数学书第17页第5题
课后作业
2.数学书第19页第7题
课后作业
3.数学书第20页第10题
课后作业
4.观察生活,提出与圆柱圆锥有关的实际问 题,并尝试解答。
课前参与
回顾与梳理本单元学习的知识、方法,用自 己喜欢的方式表达。
再见
