人教版八年级下册数学第19章一次函数复习教案

时 间 月 日 第 周 第 课时
课 题 第19章 一次函数复习 课型 复习
教学目标 1、理解一次函数的定义与图象性质。 2、理解一元一次方程、一元一次不等式、二元一次方程组与一次函数之间的关系3、使学生进一步体会“数形结合”、“方程思想”、 “待定系数法”。4、学会用函数思想解决问题,渗透数形相结合思想.
教学重点 复习巩固一次函数的图象和性质，并能简单应用运用一次函数数形相结合思想解决实际问题
教学难点 灵活运用数与形进行实际问题应用
教学设计
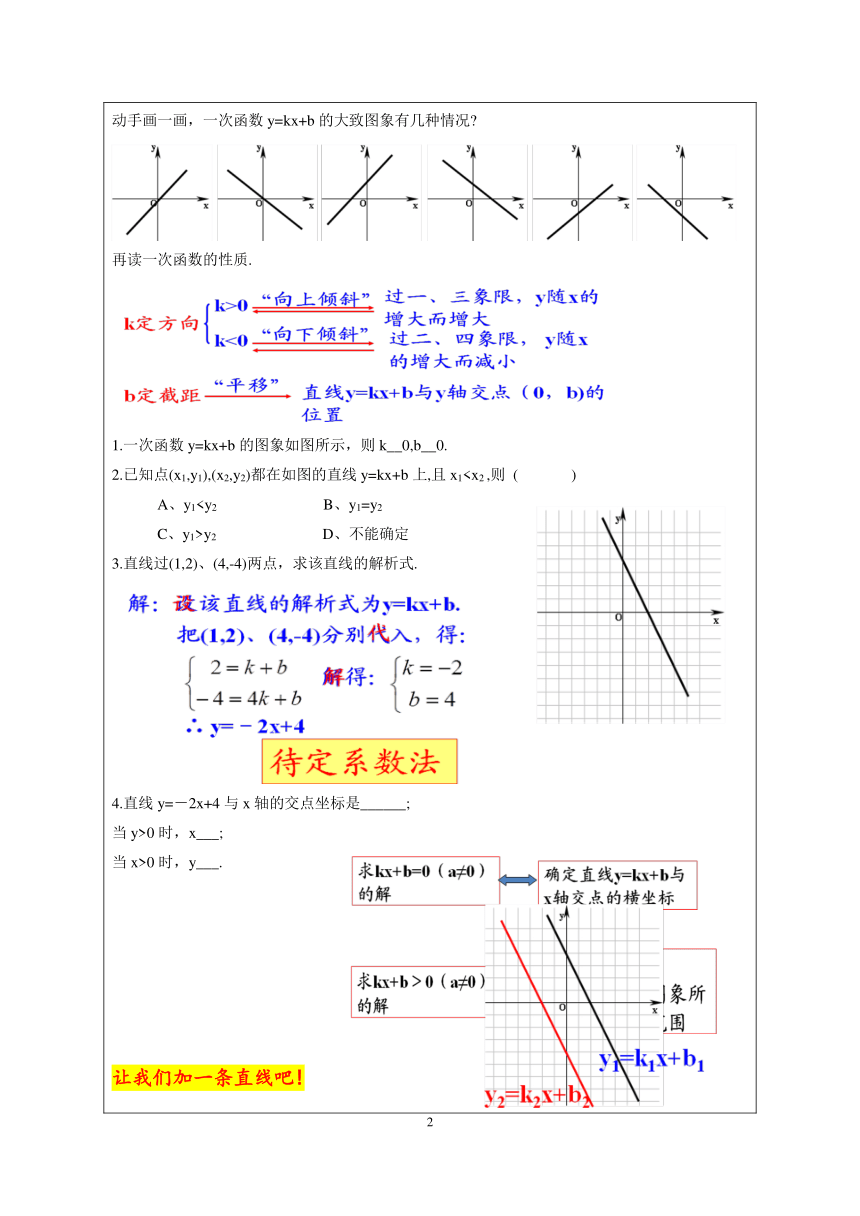
一忆定义：在心电图中，对于横坐标表示时间x的每一个确定的值，纵坐标表示心脏部位的生物电流y都有唯一确定的值与其对应吗？一般地，在一个变化过程中，如果有两个变量 x 与 y，并且对于 x 的每一个确定的值，y 都有唯一确定的值与其对应，那么我们就说 x 是自变量，y 是 x 的函数。大千世界，总在不停的运动变化中, 研究这些运动变化并寻找规律都用到了本章学习的函数.我们是从哪些方面来学习一次函数的？解析式、图象、性质、应用等.形如y=kx+b(k,b为常数,k≠0)的函数,叫做一次函数.m=_____时,函数是一次函数. 再读一次函数的解析式y=kx+b.(1)自变量的指数为1次，(2)比例系数k≠0.一次函数和正比例函数有什么联系吗？正比例函数是特殊的一次函数.二读图象：动手画一画，一次函数y=kx+b的大致图象有几种情况?再读一次函数的性质.1.一次函数y=kx+b的图象如图所示，则k__0,b__0.2.已知点(x1,y1),(x2,y2)都在如图的直线y=kx+b上,且x1y2 D、不能确定3.直线过(1,2)、(4,-4)两点，求该直线的解析式.4.直线y=－2x+4与x轴的交点坐标是______;当y>0时，x___; 当x>0时，y___. 让我们加一条直线吧!5.一次函数y=(m－1)x+(3－m)平行于直线y=2x –3，则m=_____.6.将直线y=－2x+4向下平移8个单位，得到的直线的解析式为_______.7.请依据图中给定的信息设计题目，想想两条相交直线都有哪些考核方法. 8.直线y1=－2x+4与直线y2=x+m的交点在第一象限,则m的取值范围是 .三悟应用例:在一条笔直的公路上有A、B两地，甲骑自行车从A地到B地；乙骑自行车从B地到A地，到达A地后立即按原路返回，如图是甲、乙两人离B地的距离y（km）与行驶时x（h）之间的函数图象，根据图象解答以下问题：
（1）写出A、B两地之间的距离；
（2）求出点M的坐标，并解释该点坐标所表示的实际意义
（3）若两人之间保持的距离不超过3km时，能够用无线对讲机保持联系，请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围．针对练习．由于持续高温和连日无雨，某水库的蓄水量随时间的增加而减少，已知原有蓄水量y1(万立方米)与干旱持续时间x(天)的关系如图中线段l1所示，针对这种干旱情况，从第20天开始向水库注水，注水量y2(万立方米)与时间x(天)的关系如图中线段l2所示．(不考虑其他因素) (1)求原有蓄水量y1(万立方米)与 时间x(天)的函数关系式， 并求当x＝20时的水库总蓄水量；(2)求当0≤x≤60时，水库的总蓄水量y(万立方米)与时间x(天)的函数关系式(注明x的取值 范围)，若总蓄水量不多于900万立方米为严重干旱，直接写出发生严重干旱时x的范围．归纳小结通过本节课的学习，你有何收获？你又有何疑惑？请与你的同伴交流。使你的知识更加系统化、更加条理化。相信你会做得很出色！
教学反思




4