人教版七年级下册数学课件 5.3.1 平行线的性质 (55张ppt)
文档属性
| 名称 | 人教版七年级下册数学课件 5.3.1 平行线的性质 (55张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 11.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 08:09:31 | ||
图片预览




文档简介
(共55张PPT)
平行线的性质
初一年级 数学
一、回顾梳理
问题1 上一节,我们学习了三种平行线的判定方法,请问分别
是什么?
平行线的判定方法
判定方法 1 同位角相等,两直线平行.
判定方法 2 内错角相等,两直线平行.
判定方法 3 同旁内角互补,两直线平行.
已知
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
一、回顾梳理
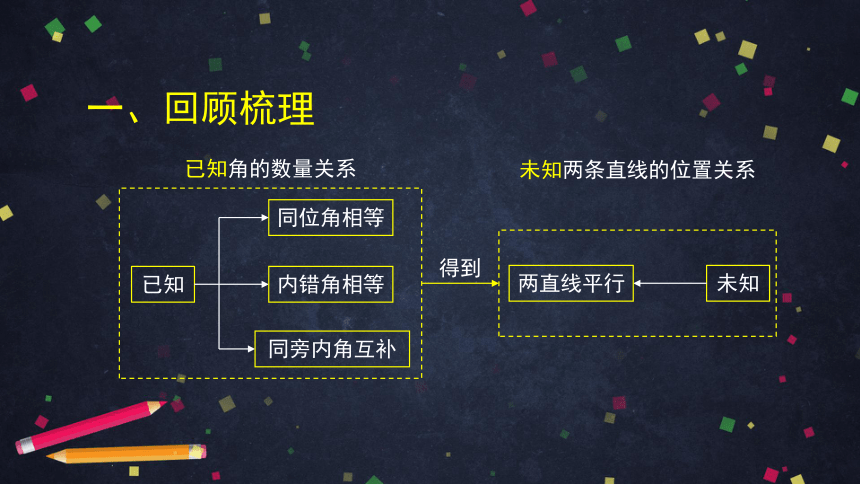
已知角的数量关系
已知
同位角相等
同旁内角互补
内错角相等
未知
两直线平行
已知角的数量关系
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
已知角的数量关系
未知
两直线平行
未知两条直线的位置关系
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
未知
两直线平行
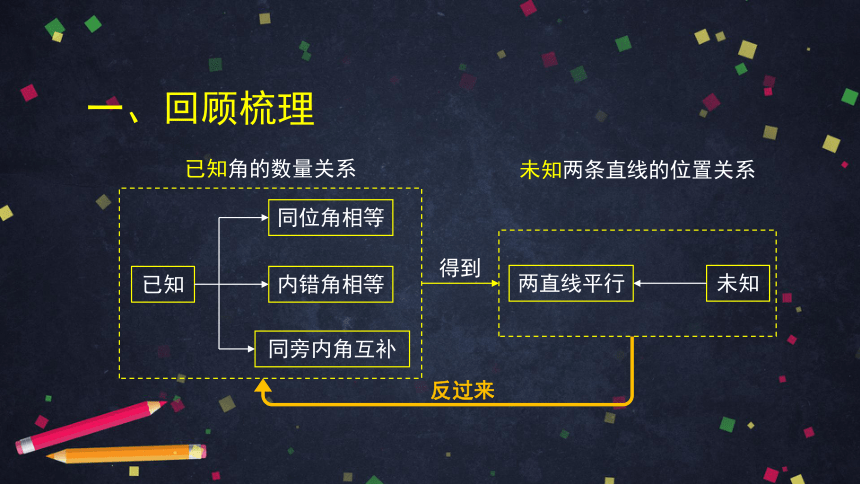
得到
已知角的数量关系
未知两条直线的位置关系
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
未知
两直线平行
得到
反过来
已知角的数量关系
未知两条直线的位置关系
一、回顾梳理
二、探究新知
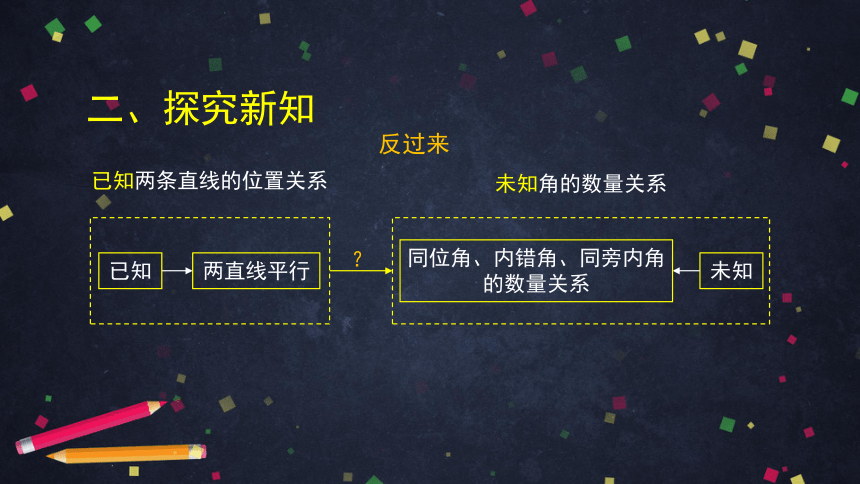
两直线平行
已知
未知
同位角、内错角、同旁内角的数量关系
反过来
未知角的数量关系
已知两条直线的位置关系
?
二、探究新知
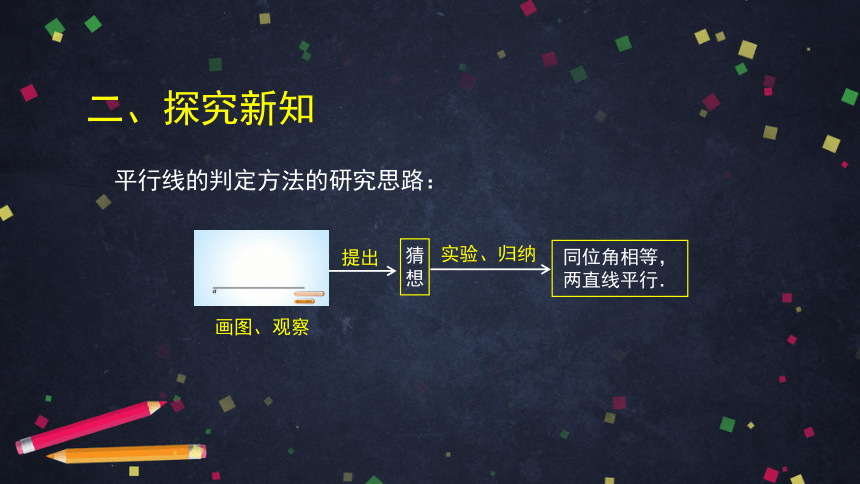
平行线的判定方法的研究思路:
画图、观察
同位角相等,
两直线平行.
实验、归纳
提出
猜
想
二、探究新知
问题2 在两条平行线被第三条直线所截,形成的同位角会具有
怎样的数量关系?
猜想:如果两条直线平行,那么同位角相等.
二、探究新知
两个角是对顶角
反过来
有两个角相等
这两个角是对顶角
×
这两个角相等
可得
验
证
如图,OC是∠AOB的角平分线.
可知,∠AOC=∠BOC.
∠AOC与∠BOC不是对顶角.
A
?
O
?
B
?
C?
二、探究新知
问题2 在两条平行线被第三条直线所截的条件下,同位角会具有
怎样的关系?
画两条平行线a∥b,然后,画一条截线c与这两条平行线相交.
如图,直线a∥b,c为截线.
a
?
b
?
c
?
二、探究新知
问题2 在两条平行线被第三条直线所截的条件下,同位角会具有
怎样的关系?
如图,直线a∥b,c为截线.
画两条平行线a∥b,然后,画一条截线c与这两条平行线相交.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
①识别图中的同位角.
②发现同位角的数量关系.
③判断在这个图中是否所有的同位角都具有相同的数量关系.
105?
75?
105?
75?
105?
75?
105?
75?
用量角器度量所形成的八个角的度数,并用表格进行整理.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
二、探究新知
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
105?
75?
105?
75?
105?
75?
105?
75?
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
105?
75?
105?
75?
105?
75?
105?
75?
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
105?
75?
105?
75?
105?
75?
105?
75?
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
105?
75?
105?
75?
105?
75?
105?
75?
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
在这个图中,两条平行线被第三条直线截得的任意一对同位角都相等.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
105?
75?
105?
75?
105?
75?
105?
75?
两直线平行,同位角相等.
特例
同位角相等
两直线平行
可得
与同位角的具体度数无关
二、探究新知
在这个图中,两条平行线被第三条直线截得的任意一对同位角都相等.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
如图,直线a∥b,d,e为截线.
9
10
11
12
d
?
1
2
3
4
a
?
b
?
e
?
5
6
7
8
二、探究新知
角
度数
角
度数
识别同位角并填入表中,让上下相邻的一对角是同位角,然后再测量度数填入表格.
13
14
15
16
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
∠9
∠10
∠11
∠12
∠13
∠14
∠15
∠16
120?
60?
120?
60?
120?
60?
120?
60?
80?
100?
80?
100?
80?
100?
80?
100?
如图,直线a∥b,d,e为截线.
9
10
11
12
13
14
15
16
d
?
1
2
3
4
a
?
b
?
e
?
同位角的度数变了,但同位角相等的数量关系不变.
二、探究新知
5
6
7
8
角
度数
角
度数
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
∠9
∠10
∠11
∠12
∠13
∠14
∠15
∠16
120?
60?
120?
60?
120?
60?
120?
60?
80?
100?
80?
100?
80?
100?
80?
100?
二、探究新知
二、探究新知
当截线的位置变化时,同位角相等的数量关系不变.
变化中的不变
二、探究新知
二、探究新知
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
如图,如果a∥b,那么∠1=∠2.
1
a
?
b
?
c
?
2
二、探究新知
平行线的性质
两直线平行
已知
同位角相等
未知
画图测量
实验
对比归纳
类比
平行线的判定
同位角相等
两直线平行
已知
未知
反
过
来
二、探究新知
研
究
思
路
梳
理
问题3 两条平行线被第三条直线截得的内错角之间有怎样的关系?
二、探究新知
同位角相等,
两直线平行.
内错角相等,
两直线平行.
推出
平行线的判定方法的探究过程:
直线a∥b
∠2=∠3
∠1=∠2
∠3与∠1互为对顶角
∠3=∠1
如图,直线a∥b,c是截线,你能由性质1,推出∠1与∠2的关系吗?
a
?
b
?
c
?
2
3
1
二、探究新知
已知
未知
联系
因为直线a∥b,
根据“两直线平行,同位角相等”,
可得∠2=∠3.
又因为∠3与∠1互为对顶角,
所以∠3=∠1.
所以∠1=∠2.
3
a
?
b
?
c
?
2
1
二、探究新知
推理过程:
平行线的性质
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
如图,如果a∥b,那么∠1=∠2.
a
?
b
?
c
?
2
1
二、探究新知
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
请同学们类比性质2的探究过程,自己试着设计探究方案,研究两条
平行线被第三条直线所截,同旁内角的数量关系.
二、探究新知
3
a
?
b
?
c
?
2
1
二、探究新知
直线a∥b
∠2=∠3
∠1+∠2=180°
∠3与∠1是邻补角
∠3+∠1=180°
如图,直线a∥b,c是截线,你能由性质1,推出∠1与∠2的关系吗?
因为直线a∥b,
根据“两直线平行,同位角相等”,
可得∠2=∠3.
又因为∠3与∠1是邻补角,
所以∠3+∠1=180°.
所以∠1+∠2=180°.
二、探究新知
3
a
?
b
?
c
?
2
1
推理过程:
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
如图,如果a∥b,那么∠1+∠2=180°.
a
?
b
?
c
?
2
1
二、探究新知
如图,直线a∥b,c是截线,根据性质2,推出∠1与∠2的关系.
a
?
b
?
c
?
2
1
3
二、探究新知
直线a∥b
∠2=∠3
∠1+∠2=180°
∠3与∠1是邻补角
∠3+∠1=180°
如图,直线a∥b,c是截线,根据性质2,推出∠1与∠2的关系.
因为直线a∥b,
根据“两直线平行,内错角相等”,
可得∠2=∠3.
又因为∠3与∠1是邻补角,
所以∠3+∠1=180°.
所以∠1+∠2=180°.
a
?
b
?
c
?
2
1
3
二、探究新知
推理过程:
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.
三、归纳提升
三、归纳提升
问题4 回顾平行线的判定与性质,说说他们的区别与联系.
可以利用图形的判定(性质)研究图形的性质(判定).
两直线
平行
同位角相等;
内错角相等;
同旁内角互补.
性质
判定
四、巩固新知
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
(2)从∠1=110°可以知道∠3是多少度?为什么?
(3)从∠1=110°可以知道∠4是多少度?为什么?
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
求得
已知 ∠1=110°
未知 ∠2的度数
联系
4
1
3
2
A
B
C
D
E
四、巩固新知
位置关系∠2与∠1是内错角
AB∥CD
数量关系∠2=∠1
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
四、巩固新知
解:因为AB∥CD,
根据“两直线平行,内错角相等”,
可得∠2=∠1.
因为∠1=110°,
所以∠2=110°.
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
四、巩固新知
位置关系∠3与∠1是同位角
AB∥CD
数量关系∠3=∠1
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(2)从∠1=110°可以知道∠3是多少度?为什么?
四、巩固新知
解:因为AB∥CD,
根据“两直线平行,同位角相等”,
可得∠3=∠1.
因为∠1=110°,
所以∠3=110°.
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(2)从∠1=110°可以知道∠3是多少度?为什么?
四、巩固新知
位置关系∠4与∠1是同旁内角
AB∥CD
数量关系∠4+∠1 =180°
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(3)从∠1=110°可以知道∠4是多少度?为什么?
四、巩固新知
4
1
3
2
A
B
C
D
E
解:因为AB∥CD,
根据“两直线平行,同旁内角互补”,
可得∠4+∠1=180°.
因为∠1=110°,
所以∠4=180?-∠1=70°.
例1 如图,平行线AB,CD被直线AE所截.
(3)从∠1=110°可以知道∠4是多少度?为什么?
四、巩固新知
平
行
线
的
性质
平
行
线
的
判
定
反过来
推理
推理
推
理
两直线平行,同旁内角互补.
两直线平行,同位角相等.
两直线平行,内错角相等.
实验探究
类比
研究思路、过程
五、课堂小结
1.如图,在四边形ABCD中,如果AD∥BC,∠A= 60°,求∠B的度数.不用度量的方法,能否求得∠D的度数?
D
A
C
B
六、课后作业
D
A
C
B
1
2
3
4
六、课后作业
2.选择题.
如图,AB∥CD ,可以得到( ).
(A)∠1=∠2 (B)∠2=∠3
(C)∠1=∠4 (D)∠3=∠4
2
3
5
4
1
?
?
a
?
b
c
d
六、课后作业
3.如图,a∥b,c,d是截线,∠1=80°,∠5=70°.∠2,∠3,∠4各是多少度?为什么?
同学们再见!
平行线的性质
初一年级 数学
一、回顾梳理
问题1 上一节,我们学习了三种平行线的判定方法,请问分别
是什么?
平行线的判定方法
判定方法 1 同位角相等,两直线平行.
判定方法 2 内错角相等,两直线平行.
判定方法 3 同旁内角互补,两直线平行.
已知
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
一、回顾梳理
已知角的数量关系
已知
同位角相等
同旁内角互补
内错角相等
未知
两直线平行
已知角的数量关系
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
已知角的数量关系
未知
两直线平行
未知两条直线的位置关系
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
未知
两直线平行
得到
已知角的数量关系
未知两条直线的位置关系
一、回顾梳理
已知
同位角相等
同旁内角互补
内错角相等
未知
两直线平行
得到
反过来
已知角的数量关系
未知两条直线的位置关系
一、回顾梳理
二、探究新知
两直线平行
已知
未知
同位角、内错角、同旁内角的数量关系
反过来
未知角的数量关系
已知两条直线的位置关系
?
二、探究新知
平行线的判定方法的研究思路:
画图、观察
同位角相等,
两直线平行.
实验、归纳
提出
猜
想
二、探究新知
问题2 在两条平行线被第三条直线所截,形成的同位角会具有
怎样的数量关系?
猜想:如果两条直线平行,那么同位角相等.
二、探究新知
两个角是对顶角
反过来
有两个角相等
这两个角是对顶角
×
这两个角相等
可得
验
证
如图,OC是∠AOB的角平分线.
可知,∠AOC=∠BOC.
∠AOC与∠BOC不是对顶角.
A
?
O
?
B
?
C?
二、探究新知
问题2 在两条平行线被第三条直线所截的条件下,同位角会具有
怎样的关系?
画两条平行线a∥b,然后,画一条截线c与这两条平行线相交.
如图,直线a∥b,c为截线.
a
?
b
?
c
?
二、探究新知
问题2 在两条平行线被第三条直线所截的条件下,同位角会具有
怎样的关系?
如图,直线a∥b,c为截线.
画两条平行线a∥b,然后,画一条截线c与这两条平行线相交.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
①识别图中的同位角.
②发现同位角的数量关系.
③判断在这个图中是否所有的同位角都具有相同的数量关系.
105?
75?
105?
75?
105?
75?
105?
75?
用量角器度量所形成的八个角的度数,并用表格进行整理.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
二、探究新知
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
105?
75?
105?
75?
105?
75?
105?
75?
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
105?
75?
105?
75?
105?
75?
105?
75?
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
105?
75?
105?
75?
105?
75?
105?
75?
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
1
2
3
4
a
?
b
?
c
?
5
6
7
8
105?
75?
105?
75?
105?
75?
105?
75?
用量角器度量所形成的八个角的度数,并用表格进行整理.
二、探究新知
在这个图中,两条平行线被第三条直线截得的任意一对同位角都相等.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
105?
75?
105?
75?
105?
75?
105?
75?
两直线平行,同位角相等.
特例
同位角相等
两直线平行
可得
与同位角的具体度数无关
二、探究新知
在这个图中,两条平行线被第三条直线截得的任意一对同位角都相等.
1
2
3
4
a
?
b
?
c
?
5
6
7
8
如图,直线a∥b,d,e为截线.
9
10
11
12
d
?
1
2
3
4
a
?
b
?
e
?
5
6
7
8
二、探究新知
角
度数
角
度数
识别同位角并填入表中,让上下相邻的一对角是同位角,然后再测量度数填入表格.
13
14
15
16
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
∠9
∠10
∠11
∠12
∠13
∠14
∠15
∠16
120?
60?
120?
60?
120?
60?
120?
60?
80?
100?
80?
100?
80?
100?
80?
100?
如图,直线a∥b,d,e为截线.
9
10
11
12
13
14
15
16
d
?
1
2
3
4
a
?
b
?
e
?
同位角的度数变了,但同位角相等的数量关系不变.
二、探究新知
5
6
7
8
角
度数
角
度数
∠1
∠2
∠3
∠4
∠5
∠6
∠7
∠8
∠9
∠10
∠11
∠12
∠13
∠14
∠15
∠16
120?
60?
120?
60?
120?
60?
120?
60?
80?
100?
80?
100?
80?
100?
80?
100?
二、探究新知
二、探究新知
当截线的位置变化时,同位角相等的数量关系不变.
变化中的不变
二、探究新知
二、探究新知
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
简单说成:两直线平行,同位角相等.
如图,如果a∥b,那么∠1=∠2.
1
a
?
b
?
c
?
2
二、探究新知
平行线的性质
两直线平行
已知
同位角相等
未知
画图测量
实验
对比归纳
类比
平行线的判定
同位角相等
两直线平行
已知
未知
反
过
来
二、探究新知
研
究
思
路
梳
理
问题3 两条平行线被第三条直线截得的内错角之间有怎样的关系?
二、探究新知
同位角相等,
两直线平行.
内错角相等,
两直线平行.
推出
平行线的判定方法的探究过程:
直线a∥b
∠2=∠3
∠1=∠2
∠3与∠1互为对顶角
∠3=∠1
如图,直线a∥b,c是截线,你能由性质1,推出∠1与∠2的关系吗?
a
?
b
?
c
?
2
3
1
二、探究新知
已知
未知
联系
因为直线a∥b,
根据“两直线平行,同位角相等”,
可得∠2=∠3.
又因为∠3与∠1互为对顶角,
所以∠3=∠1.
所以∠1=∠2.
3
a
?
b
?
c
?
2
1
二、探究新知
推理过程:
平行线的性质
性质2 两条平行线被第三条直线所截,内错角相等.
简单说成:两直线平行,内错角相等.
如图,如果a∥b,那么∠1=∠2.
a
?
b
?
c
?
2
1
二、探究新知
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
请同学们类比性质2的探究过程,自己试着设计探究方案,研究两条
平行线被第三条直线所截,同旁内角的数量关系.
二、探究新知
3
a
?
b
?
c
?
2
1
二、探究新知
直线a∥b
∠2=∠3
∠1+∠2=180°
∠3与∠1是邻补角
∠3+∠1=180°
如图,直线a∥b,c是截线,你能由性质1,推出∠1与∠2的关系吗?
因为直线a∥b,
根据“两直线平行,同位角相等”,
可得∠2=∠3.
又因为∠3与∠1是邻补角,
所以∠3+∠1=180°.
所以∠1+∠2=180°.
二、探究新知
3
a
?
b
?
c
?
2
1
推理过程:
性质3 两条平行线被第三条直线所截,同旁内角互补.
简单说成:两直线平行,同旁内角互补.
如图,如果a∥b,那么∠1+∠2=180°.
a
?
b
?
c
?
2
1
二、探究新知
如图,直线a∥b,c是截线,根据性质2,推出∠1与∠2的关系.
a
?
b
?
c
?
2
1
3
二、探究新知
直线a∥b
∠2=∠3
∠1+∠2=180°
∠3与∠1是邻补角
∠3+∠1=180°
如图,直线a∥b,c是截线,根据性质2,推出∠1与∠2的关系.
因为直线a∥b,
根据“两直线平行,内错角相等”,
可得∠2=∠3.
又因为∠3与∠1是邻补角,
所以∠3+∠1=180°.
所以∠1+∠2=180°.
a
?
b
?
c
?
2
1
3
二、探究新知
推理过程:
平行线的性质
性质1 两条平行线被第三条直线所截,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.
三、归纳提升
三、归纳提升
问题4 回顾平行线的判定与性质,说说他们的区别与联系.
可以利用图形的判定(性质)研究图形的性质(判定).
两直线
平行
同位角相等;
内错角相等;
同旁内角互补.
性质
判定
四、巩固新知
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
(2)从∠1=110°可以知道∠3是多少度?为什么?
(3)从∠1=110°可以知道∠4是多少度?为什么?
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
求得
已知 ∠1=110°
未知 ∠2的度数
联系
4
1
3
2
A
B
C
D
E
四、巩固新知
位置关系∠2与∠1是内错角
AB∥CD
数量关系∠2=∠1
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
四、巩固新知
解:因为AB∥CD,
根据“两直线平行,内错角相等”,
可得∠2=∠1.
因为∠1=110°,
所以∠2=110°.
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(1)从∠1=110°可以知道∠2是多少度?为什么?
四、巩固新知
位置关系∠3与∠1是同位角
AB∥CD
数量关系∠3=∠1
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(2)从∠1=110°可以知道∠3是多少度?为什么?
四、巩固新知
解:因为AB∥CD,
根据“两直线平行,同位角相等”,
可得∠3=∠1.
因为∠1=110°,
所以∠3=110°.
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(2)从∠1=110°可以知道∠3是多少度?为什么?
四、巩固新知
位置关系∠4与∠1是同旁内角
AB∥CD
数量关系∠4+∠1 =180°
4
1
3
2
A
B
C
D
E
例1 如图,平行线AB,CD被直线AE所截.
(3)从∠1=110°可以知道∠4是多少度?为什么?
四、巩固新知
4
1
3
2
A
B
C
D
E
解:因为AB∥CD,
根据“两直线平行,同旁内角互补”,
可得∠4+∠1=180°.
因为∠1=110°,
所以∠4=180?-∠1=70°.
例1 如图,平行线AB,CD被直线AE所截.
(3)从∠1=110°可以知道∠4是多少度?为什么?
四、巩固新知
平
行
线
的
性质
平
行
线
的
判
定
反过来
推理
推理
推
理
两直线平行,同旁内角互补.
两直线平行,同位角相等.
两直线平行,内错角相等.
实验探究
类比
研究思路、过程
五、课堂小结
1.如图,在四边形ABCD中,如果AD∥BC,∠A= 60°,求∠B的度数.不用度量的方法,能否求得∠D的度数?
D
A
C
B
六、课后作业
D
A
C
B
1
2
3
4
六、课后作业
2.选择题.
如图,AB∥CD ,可以得到( ).
(A)∠1=∠2 (B)∠2=∠3
(C)∠1=∠4 (D)∠3=∠4
2
3
5
4
1
?
?
a
?
b
c
d
六、课后作业
3.如图,a∥b,c,d是截线,∠1=80°,∠5=70°.∠2,∠3,∠4各是多少度?为什么?
同学们再见!
