人教版七年级下册数学课件5.3.1 平行线的性质的应用 (39张ppt)
文档属性
| 名称 | 人教版七年级下册数学课件5.3.1 平行线的性质的应用 (39张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 00:00:00 | ||
图片预览



文档简介
(共39张PPT)
平行线的性质的应用
初一年级 数学
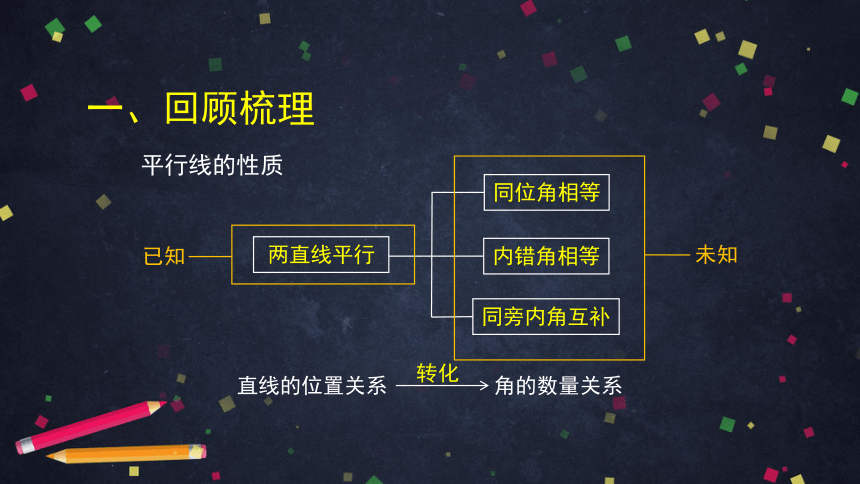
一、回顾梳理
性质1 两条平行线被第三条直线所截,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.
学习了平行线的性质后,我们能解决什么问题?
问题1 平行线的三条性质分别是什么?
同旁内角互补
同位角相等
内错角相等
两直线平行
一、回顾梳理
平行线的性质
未知
已知
直线的位置关系
角的数量关系
转化
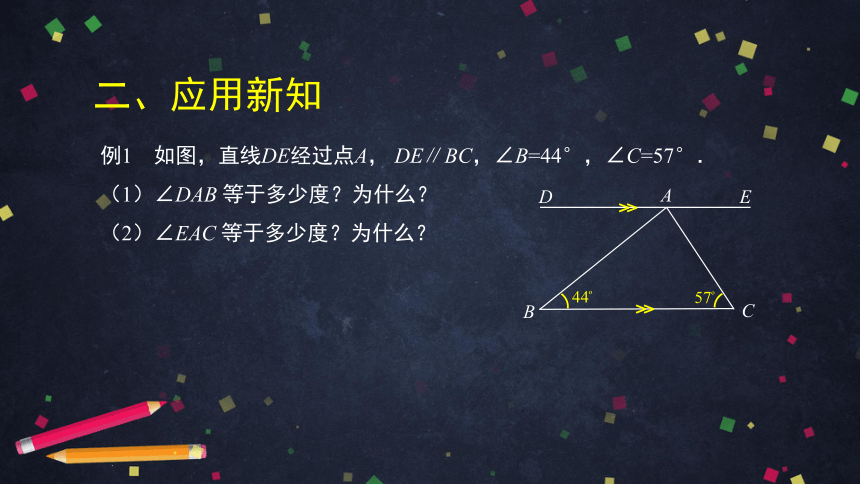
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
(2)∠EAC 等于多少度?为什么?
A
D
E
B
C
44?
57?
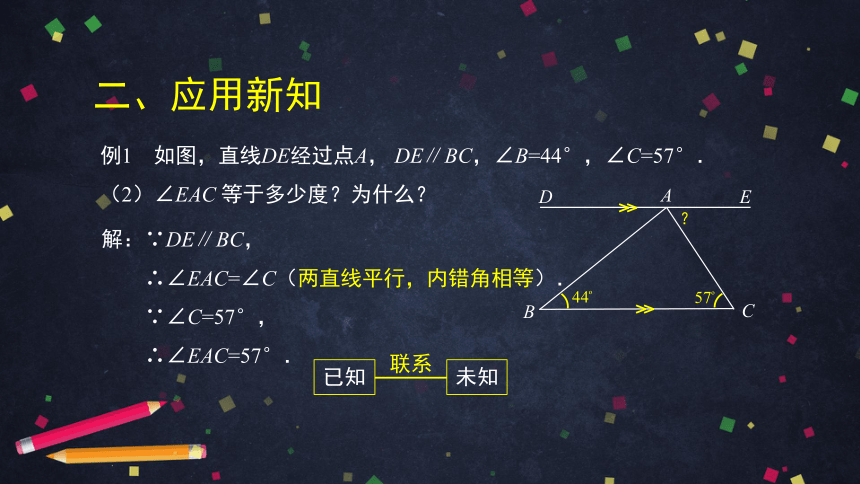
二、应用新知
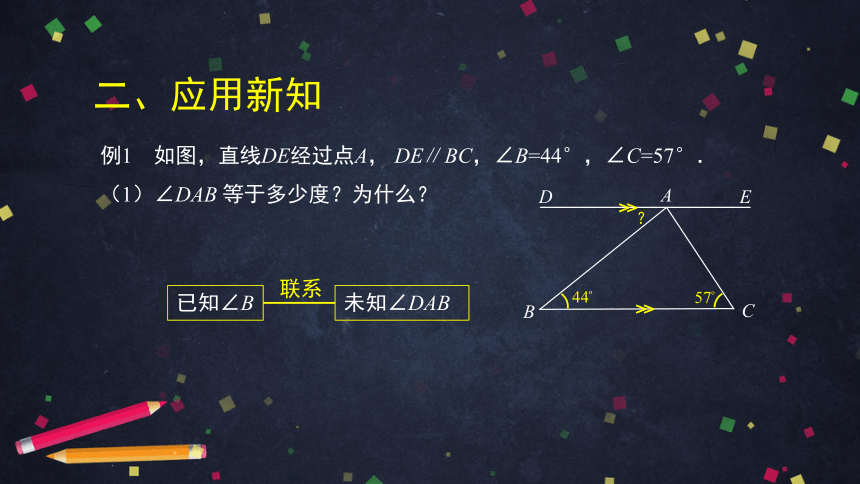
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
二、应用新知
?
已知∠B
未知∠DAB
联系
A
D
E
B
C
44?
57?
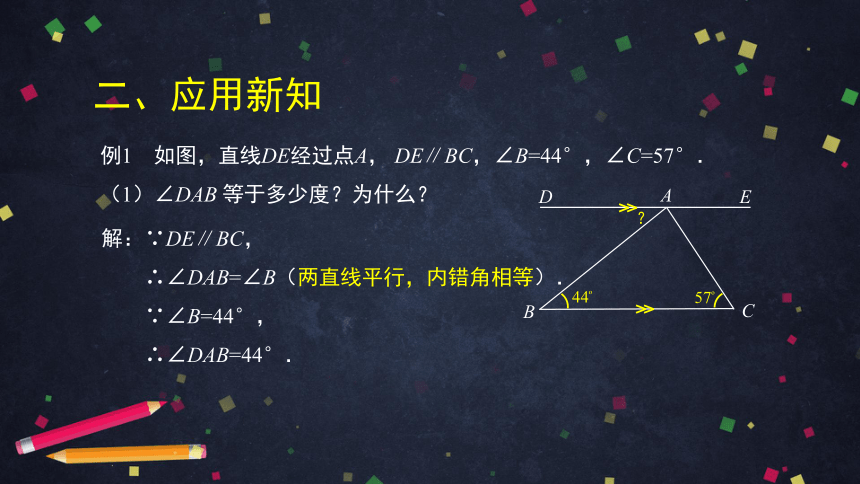
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
解:∵DE∥BC,
∴∠DAB=∠B(两直线平行,内错角相等).
∵∠B=44°,
∴∠DAB=44°.
二、应用新知
?
A
D
E
B
C
44?
57?
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(2)∠EAC 等于多少度?为什么?
二、应用新知
?
已知
未知
联系
解:∵DE∥BC,
∴∠EAC=∠C(两直线平行,内错角相等).
∵∠C=57°,
∴∠EAC=57°.
A
D
E
B
C
44?
57?
A
B
C
D
E
60?
60?
40?
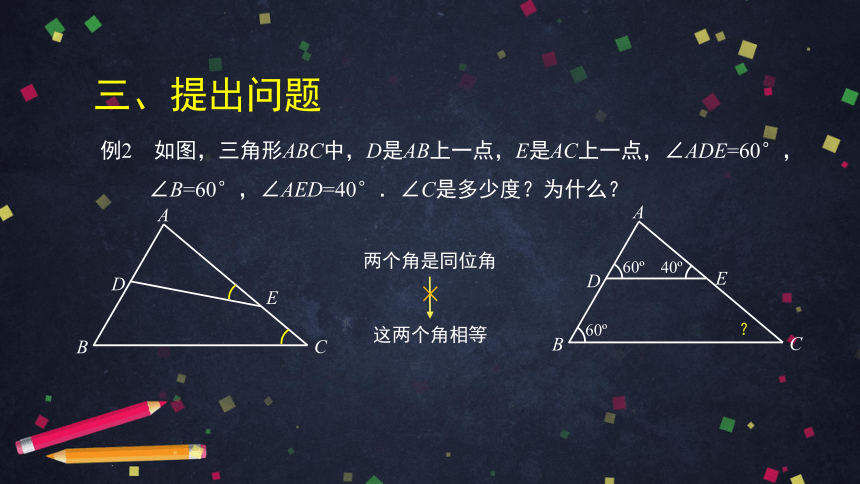
三、提出问题
?
A
B
C
D
E
两个角是同位角
这两个角相等
×
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
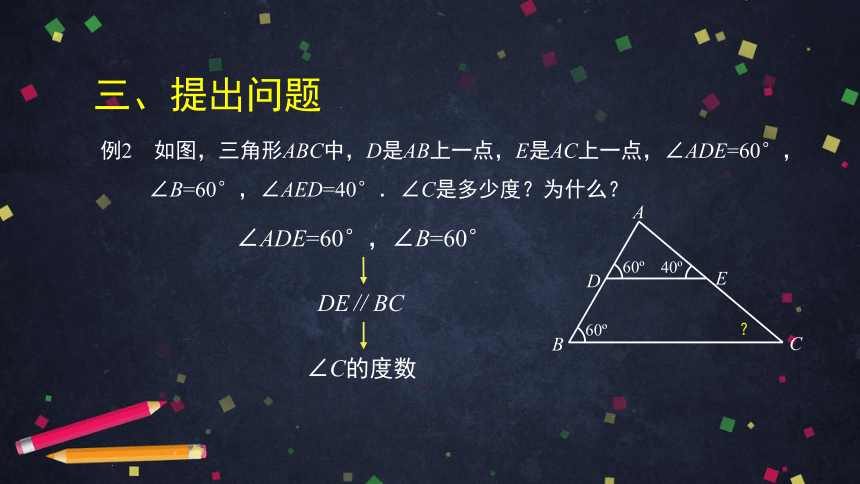
三、提出问题
A
B
C
D
E
60?
60?
40?
?
∠C的度数
∠ADE=60°,∠B=60°
DE∥BC
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
解:∵∠ADE=60°,∠B=60°(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠C=∠AED(两直线平行,同位角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
三、提出问题
A
B
C
D
E
60?
60?
40?
?
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
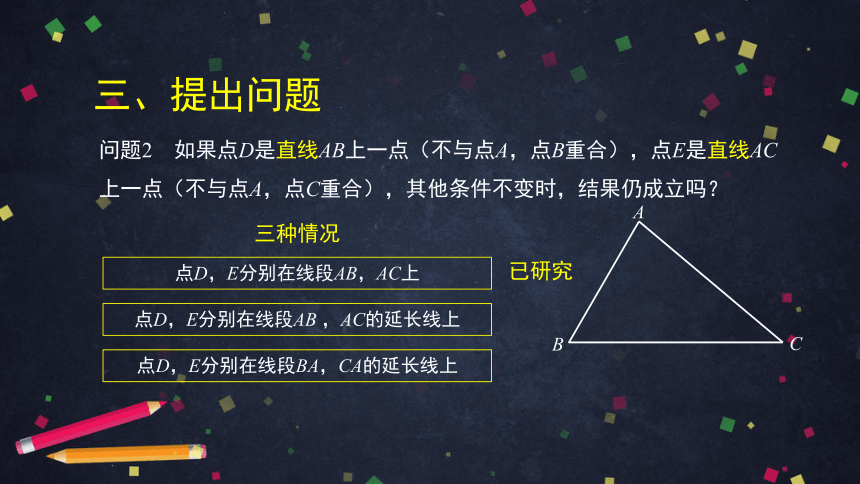
三、提出问题
点D,E分别在线段AB,AC上
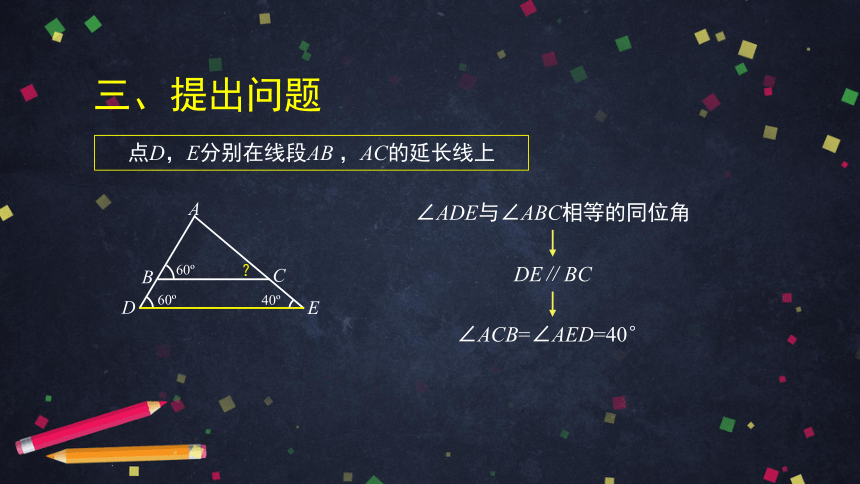
点D,E分别在线段AB ,AC的延长线上
点D,E分别在线段BA,CA的延长线上
三种情况
已研究
问题2 如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立吗?
A
B
C
三、提出问题
60?
60?
E
A
B
C
D
∠ADE与∠ABC相等的同位角
DE∥BC
40?
∠ACB=∠AED=40°
?
点D,E分别在线段AB ,AC的延长线上
三、提出问题
A
B
C
D
E
60?
60?
40?
?
点D,E分别在线段BA ,CA的延长线上
∠C的度数
∠ADE=60°,∠B=60°
DE∥BC
三、提出问题
解:∵ ∠ADE=60°,∠B=60°(已知),
∴ ∠ADE=∠B(等量代换).
∴ DE∥BC(内错角相等,两直线平行).
∴∠C=∠AED(两直线平行,内错角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
A
B
C
D
E
60?
60?
40?
?
点D,E分别在线段BA ,CA的延长线上
三、提出问题
同位角
同位角
内错角
A
B
C
D
E
图1
A
B
C
D
E
图2
图3
A
B
C
D
E
如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立.
四、拓展提升
如图, AB∥CD,GH分别交AB和CD于点E和点M ,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
猜想EF∥MN
例3 两条平行线被第三条直线所截,形成的任意一组同位角的角平分线
具有怎样的位置关系?
A
G
H
C
M
D
B
N
E
F
F
F
E
M
N
四、拓展提升
EF∥MN
∠ .= ∠ .或∠ .+∠ . =180°
.
A
G
H
C
M
D
B
N
E
F
N
F
E
M
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
EF∥MN
∠ = ∠ .
A
G
H
C
M
D
B
N
E
F
N
F
E
M
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
A
G
H
B
C
D
F
N
E
M
N
B
F
D
E
M
EF∥MN
∠ = ∠ .
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
AB∥CD
A
G
H
C
M
∠GEB=∠EMD
角平分线
EF∥MN
D
B
N
E
F
1
2
1
2
∠ =∠ .
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
解:∵AB∥CD,
∴∠GEB=∠EMD.
∵EF是∠GEB的角平分线,
MN是∠EMD的角平分线,
∴∠1=∠2.
∴EF∥MN.
∴
,
.
A
G
H
C
M
D
B
N
E
F
1
2
四、拓展提升
A
G
H
B
C
D
F
N
E
M
A
G
H
B
C
D
F
N
E
M
猜想EF∥MN
猜想EF⊥MN
问题3 两条平行线被第三条直线所截,形成的任意一组内错角或同旁内角的角平分线具有怎样的位置关系?
例4 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
五、实际应用
研究几何图形的数量关系、位置关系.
C
D
B
A
C
D
100?
115?
B
A
五、实际应用
D
梯形ABCD
∠A与∠D是同旁内角
∠B与∠C是同旁内角
AB∥CD
∠D与∠A互补
∠C与∠B互补
如图,在梯形ABCD中,∠A=100°,∠B=115°,求∠C与∠D的度数.
B
A
?
?
解:因为梯形上、下两底AB与CD互相平行,
根据“两直线平行,同旁内角互补”,
可得∠A与∠D互补,∠B与∠C互补.
于是
∠D=180?-∠A=180°-100°=80°,
∠C=180?-∠B=180°-115°=65°.
所以梯形的另外两个角分别为80°,65°.
五、实际应用
C
D
100?
115?
B
A
D
如图,在梯形ABCD中,∠A=100°,∠B=115°,求∠C与∠D的度数.
练习 潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时∠1=∠2, ∠3=∠4, 进入潜望镜的光线和离开潜望镜的光线是什么关系?
光
线
1
2
3
4
五、实际应用
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
AB∥CD
∠ .= ∠ .或∠ .+∠ . =180°
.
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
AB∥CD
∠ .= ∠ .或∠ .+∠ . =180°
.
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
5
6
AB∥CD
∠ .= ∠ .或∠ .+∠ . =180°
.
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
5
6
转化
AB∥CD
∠5=∠6
4
1
2
3
5
6
B
A
C
D
E
F
G
H
五、实际应用
AB∥CD
∠5=∠6
EF∥GH
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
5
6
B
A
C
D
E
F
G
H
五、实际应用
EF∥GH
AB∥CD
∠5=∠6
∠2=∠3
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
5
6
B
A
C
D
E
F
G
H
五、实际应用
证明:∵ EF∥GH,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4.
∵∠5=180°-∠1-∠2,∠6=180°-∠3-∠4,
∴∠5=∠6.
∴AB∥CD(内错角相等,两直线平行).
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
过程梳理
实际问题
数学问题
抽象
解决数学问题
观察
分析
推理
解
决
画图
五、实际应用
六、课堂小结
已知、未知是什么?条件是什么?
能否借助条件让已知与未知产生联系?
以前是否解决过类似问题?能否类比进行求解?
在解决问题时,我们可以这样进行思考:
已知
未知
联系
想可知
想需知
六、课堂小结
这个问题的解决思路是什么?能用这种思路解决什么类型的问题?
在解决这个问题时,关键在哪里?自己是如何突破的?
改变问题中的部分条件,结果还成立吗?
得到的结论具有一般性吗?
在解决问题后,我们可以进行这样的反思:
1.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,第二次的拐角∠B是多少度?为什么?
A
B
七、课后作业
2.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
8
7
6
5
4
3
2
1
水
空气
七、课后作业
同学们再见!
平行线的性质的应用
初一年级 数学
一、回顾梳理
性质1 两条平行线被第三条直线所截,同位角相等.
性质2 两条平行线被第三条直线所截,内错角相等.
性质3 两条平行线被第三条直线所截,同旁内角互补.
学习了平行线的性质后,我们能解决什么问题?
问题1 平行线的三条性质分别是什么?
同旁内角互补
同位角相等
内错角相等
两直线平行
一、回顾梳理
平行线的性质
未知
已知
直线的位置关系
角的数量关系
转化
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
(2)∠EAC 等于多少度?为什么?
A
D
E
B
C
44?
57?
二、应用新知
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
二、应用新知
?
已知∠B
未知∠DAB
联系
A
D
E
B
C
44?
57?
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(1)∠DAB 等于多少度?为什么?
解:∵DE∥BC,
∴∠DAB=∠B(两直线平行,内错角相等).
∵∠B=44°,
∴∠DAB=44°.
二、应用新知
?
A
D
E
B
C
44?
57?
例1 如图,直线DE经过点A, DE∥BC,∠B=44°,∠C=57°.
(2)∠EAC 等于多少度?为什么?
二、应用新知
?
已知
未知
联系
解:∵DE∥BC,
∴∠EAC=∠C(两直线平行,内错角相等).
∵∠C=57°,
∴∠EAC=57°.
A
D
E
B
C
44?
57?
A
B
C
D
E
60?
60?
40?
三、提出问题
?
A
B
C
D
E
两个角是同位角
这两个角相等
×
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
三、提出问题
A
B
C
D
E
60?
60?
40?
?
∠C的度数
∠ADE=60°,∠B=60°
DE∥BC
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
解:∵∠ADE=60°,∠B=60°(已知),
∴∠ADE=∠B(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠C=∠AED(两直线平行,同位角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
三、提出问题
A
B
C
D
E
60?
60?
40?
?
例2 如图,三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,
∠B=60°,∠AED=40°.∠C是多少度?为什么?
三、提出问题
点D,E分别在线段AB,AC上
点D,E分别在线段AB ,AC的延长线上
点D,E分别在线段BA,CA的延长线上
三种情况
已研究
问题2 如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立吗?
A
B
C
三、提出问题
60?
60?
E
A
B
C
D
∠ADE与∠ABC相等的同位角
DE∥BC
40?
∠ACB=∠AED=40°
?
点D,E分别在线段AB ,AC的延长线上
三、提出问题
A
B
C
D
E
60?
60?
40?
?
点D,E分别在线段BA ,CA的延长线上
∠C的度数
∠ADE=60°,∠B=60°
DE∥BC
三、提出问题
解:∵ ∠ADE=60°,∠B=60°(已知),
∴ ∠ADE=∠B(等量代换).
∴ DE∥BC(内错角相等,两直线平行).
∴∠C=∠AED(两直线平行,内错角相等).
∵∠AED=40°(已知),
∴∠C=40°(等量代换).
A
B
C
D
E
60?
60?
40?
?
点D,E分别在线段BA ,CA的延长线上
三、提出问题
同位角
同位角
内错角
A
B
C
D
E
图1
A
B
C
D
E
图2
图3
A
B
C
D
E
如果点D是直线AB上一点(不与点A,点B重合),点E是直线AC上一点(不与点A,点C重合),其他条件不变时,结果仍成立.
四、拓展提升
如图, AB∥CD,GH分别交AB和CD于点E和点M ,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
猜想EF∥MN
例3 两条平行线被第三条直线所截,形成的任意一组同位角的角平分线
具有怎样的位置关系?
A
G
H
C
M
D
B
N
E
F
F
F
E
M
N
四、拓展提升
EF∥MN
∠ .= ∠ .或∠ .+∠ . =180°
.
A
G
H
C
M
D
B
N
E
F
N
F
E
M
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
EF∥MN
∠ = ∠ .
A
G
H
C
M
D
B
N
E
F
N
F
E
M
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
A
G
H
B
C
D
F
N
E
M
N
B
F
D
E
M
EF∥MN
∠ = ∠ .
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
AB∥CD
A
G
H
C
M
∠GEB=∠EMD
角平分线
EF∥MN
D
B
N
E
F
1
2
1
2
∠ =∠ .
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
四、拓展提升
如图,AB∥CD,GH分别交AB和CD于点E和点M,EF是∠GEB的角平分线,MN是∠EMD的角平分线.
解:∵AB∥CD,
∴∠GEB=∠EMD.
∵EF是∠GEB的角平分线,
MN是∠EMD的角平分线,
∴∠1=∠2.
∴EF∥MN.
∴
,
.
A
G
H
C
M
D
B
N
E
F
1
2
四、拓展提升
A
G
H
B
C
D
F
N
E
M
A
G
H
B
C
D
F
N
E
M
猜想EF∥MN
猜想EF⊥MN
问题3 两条平行线被第三条直线所截,形成的任意一组内错角或同旁内角的角平分线具有怎样的位置关系?
例4 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
五、实际应用
研究几何图形的数量关系、位置关系.
C
D
B
A
C
D
100?
115?
B
A
五、实际应用
D
梯形ABCD
∠A与∠D是同旁内角
∠B与∠C是同旁内角
AB∥CD
∠D与∠A互补
∠C与∠B互补
如图,在梯形ABCD中,∠A=100°,∠B=115°,求∠C与∠D的度数.
B
A
?
?
解:因为梯形上、下两底AB与CD互相平行,
根据“两直线平行,同旁内角互补”,
可得∠A与∠D互补,∠B与∠C互补.
于是
∠D=180?-∠A=180°-100°=80°,
∠C=180?-∠B=180°-115°=65°.
所以梯形的另外两个角分别为80°,65°.
五、实际应用
C
D
100?
115?
B
A
D
如图,在梯形ABCD中,∠A=100°,∠B=115°,求∠C与∠D的度数.
练习 潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时∠1=∠2, ∠3=∠4, 进入潜望镜的光线和离开潜望镜的光线是什么关系?
光
线
1
2
3
4
五、实际应用
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
AB∥CD
∠ .= ∠ .或∠ .+∠ . =180°
.
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
AB∥CD
∠ .= ∠ .或∠ .+∠ . =180°
.
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
5
6
AB∥CD
∠ .= ∠ .或∠ .+∠ . =180°
.
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
B
A
C
D
E
F
G
H
五、实际应用
5
6
转化
AB∥CD
∠5=∠6
4
1
2
3
5
6
B
A
C
D
E
F
G
H
五、实际应用
AB∥CD
∠5=∠6
EF∥GH
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
5
6
B
A
C
D
E
F
G
H
五、实际应用
EF∥GH
AB∥CD
∠5=∠6
∠2=∠3
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
4
1
2
3
5
6
B
A
C
D
E
F
G
H
五、实际应用
证明:∵ EF∥GH,
∴∠2=∠3(两直线平行,内错角相等).
∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4.
∵∠5=180°-∠1-∠2,∠6=180°-∠3-∠4,
∴∠5=∠6.
∴AB∥CD(内错角相等,两直线平行).
如图,EF∥GH,∠1= ∠2,∠3= ∠4.
判断AB与CD的位置关系并说明理由.
过程梳理
实际问题
数学问题
抽象
解决数学问题
观察
分析
推理
解
决
画图
五、实际应用
六、课堂小结
已知、未知是什么?条件是什么?
能否借助条件让已知与未知产生联系?
以前是否解决过类似问题?能否类比进行求解?
在解决问题时,我们可以这样进行思考:
已知
未知
联系
想可知
想需知
六、课堂小结
这个问题的解决思路是什么?能用这种思路解决什么类型的问题?
在解决这个问题时,关键在哪里?自己是如何突破的?
改变问题中的部分条件,结果还成立吗?
得到的结论具有一般性吗?
在解决问题后,我们可以进行这样的反思:
1.如图,一条公路两次转弯后,和原来的方向相同.如果第一次的拐角∠A是135°,第二次的拐角∠B是多少度?为什么?
A
B
七、课后作业
2.光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气时,要发生折射.由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图,∠1=45°,∠2=122°,求图中其他角的度数.
8
7
6
5
4
3
2
1
水
空气
七、课后作业
同学们再见!
