北京版数学七年级下册 第四章一元一次不等式和一元一次不等式组复习(第一课时) 课件 (共51张PPT)
文档属性
| 名称 | 北京版数学七年级下册 第四章一元一次不等式和一元一次不等式组复习(第一课时) 课件 (共51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 00:00:00 | ||
图片预览





文档简介
(共51张PPT)
初一年级 数学
一元一次不等式和一元一次不等式组复习(第一课时)
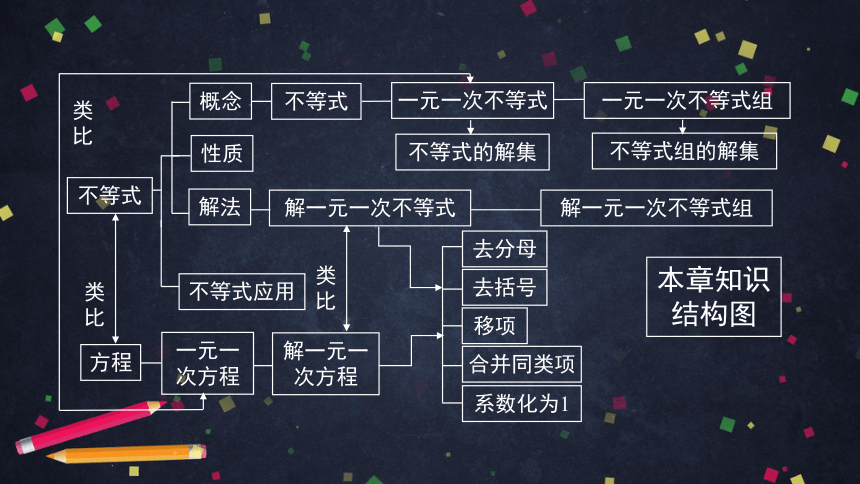
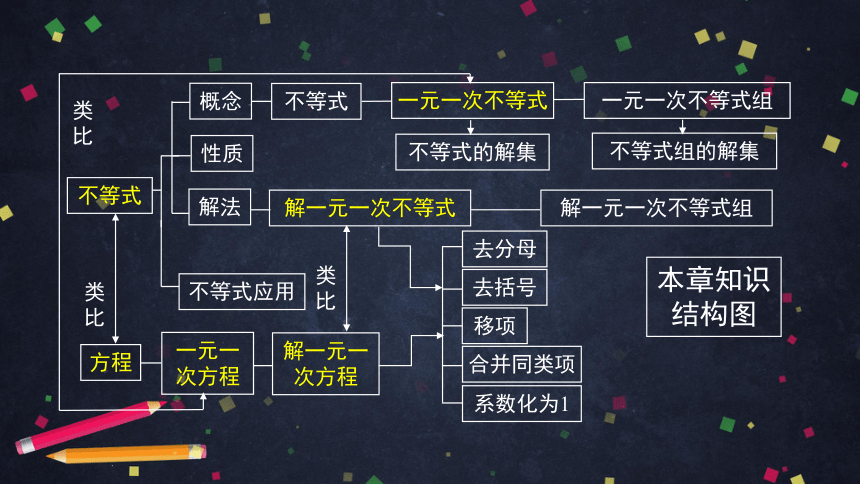
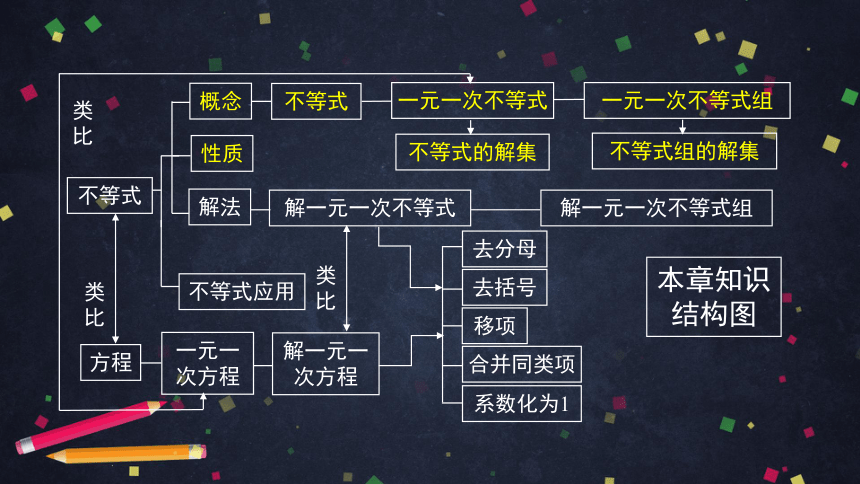
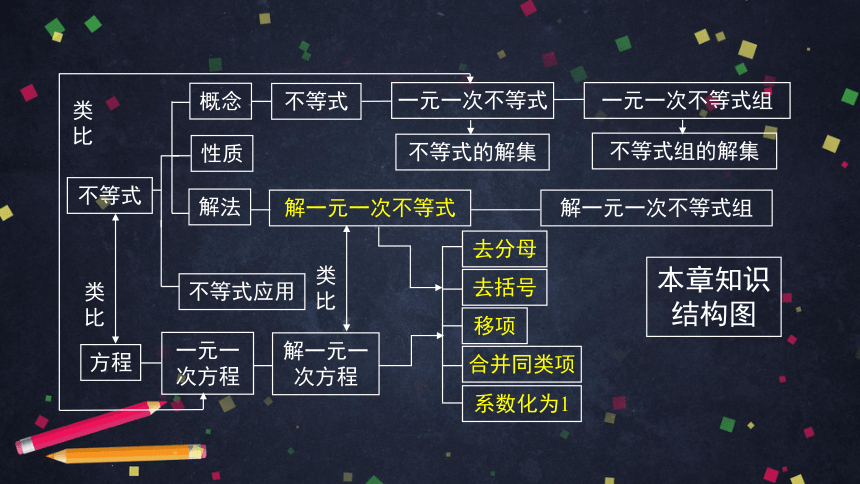
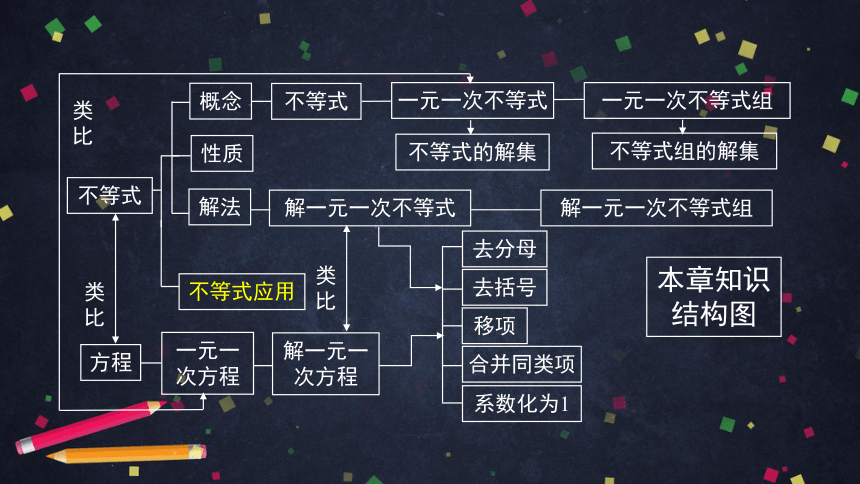
不等式
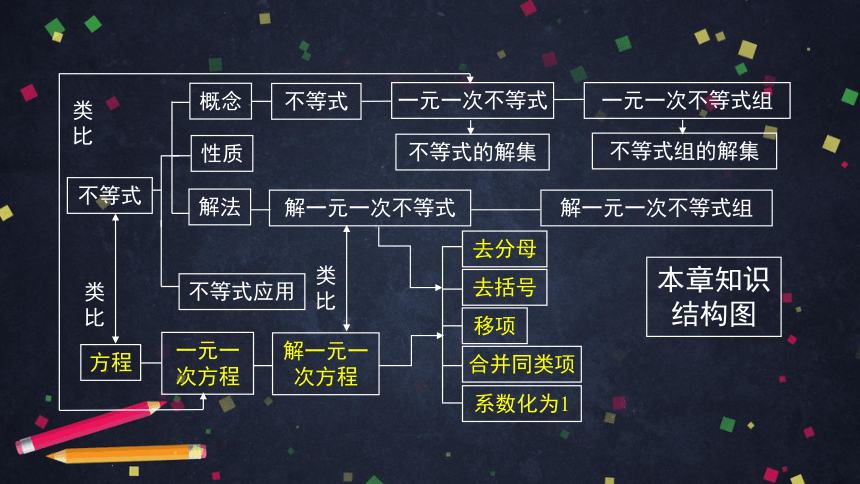
去分母
一元一次不等式
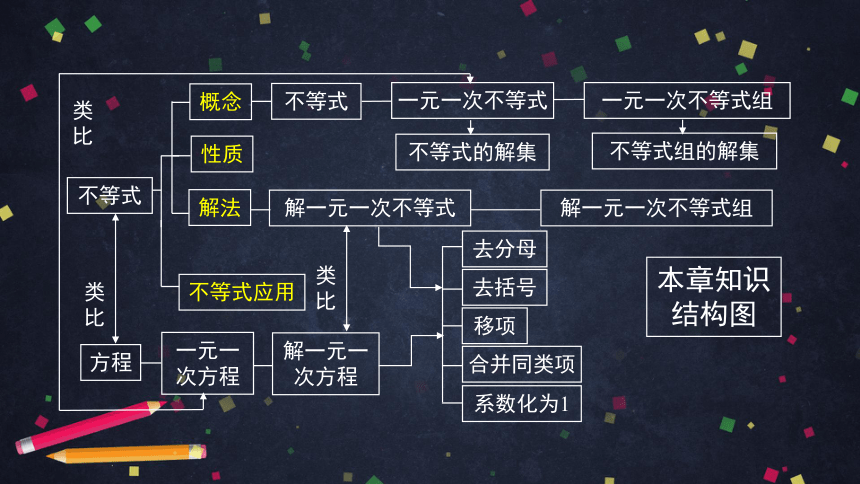
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
一、不等式的概念
知识概要
用不等号表示不等关系的式子叫做不等式.
表示不等关系的符号:>、<、≥、≤、≠.
表示不等关系的语言:大于、小于、不大于、不少于…
还有一些常见的数学术语:正数、负数、非负数.
一、不等式的概念
知识概要
用不等号表示不等关系的式子叫做不等式.
下列各式是不等式的有( )
① ;
② ;
③ ;
④ ;
⑤ ;
①,②,④,⑥
⑥ .
≤
二、不等式的基本性质
知识概要
1.不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变;
如果a>b ,那么 a±c>b±c .
2.不等式两边都乘(或除以)同一个正数,不等号的方向不变;
如果a>b ,c>0,那么ac>bc(或 ) .
二、不等式的基本性质
知识概要
3.不等式两边都乘(或除以)同一个负数,不等号的方向改变.
如果a>b , c<0 ,那么ac<bc (或 ) .
例1 设 x>y ,用“>”或“<”填空:
;
;
;
.
例1 设 x>y ,用“>”或“<”填空:
;
>
不等式的基本性质1
例1 设 x>y ,用“>”或“<”填空:
>
;
;
>
不等式的基本性质2
例1 设 x>y ,用“>”或“<”填空:
>
>
;
;
;
再根据不等式的基本性质1
先根据不等式的基本性质2
>
例1 设 x>y ,用“>”或“<”填空:
>
>
;
;
;
再根据不等式的基本性质2
先根据不等式的基本性质1
>
例1 设 x>y ,用“>”或“<”填空:
>
>
>
;
;
;
.
<
再根据不等式的基本性质1
先根据不等式的基本性质3
例1 设 x>y ,用“>”或“<”填空:
>
<
>
>
思考:若x>y ,则 .
当a=0时, a2=0,
当a表示正数,即a>0时,
当a表示负数,即a<0时,
;
;
;
.
a2>0,
a2x> a2y;
a2>0,
a2x> a2y .
a2x= a2y;
≥
三、不等式的解
知识概要
使不等式成立的未知数的值叫做不等式的解.
四、不等式的解集
一个不等式的所有解组成的集合叫做这个不等式的解集.
五、一元一次不等式
知识概要
只含有一个未知数,并且未知数的最高次数是1,系数不等于0,这样的不等式叫做一元一次不等式.
解不等式就是求不等式解集的过程.就是利用不等式的基本性质将不等式化为x>a或x 例2 已知关于x的不等式(1-m )x<2的解集为x> ,求m的取值范围.
对比: (1-m )x 2
x
不等式的基本性质3 ,
不等号的方向发生了改变,由此你想到了什么?
<
>
这里1-m<0 .
例2 已知关于x的不等式(1-m )x<2的解集为x> ,求m的取值范围.
解:因为不等号的方向发生了改变,
利用的是不
等式的基本性质3,
所以不等式两边同时除以(1-m ),
这里1-m<0 , m>1 .
所以m的取值范围是m>1 .
不等式的基本性质的应用一般有两种:
1.已知变形方式,依据不等式的基本性质确定不等号的方向;
2.已知变形结果,依据不等号的方向确定不等式的基本性质
例2 关于x的不等式(1-m )x<2的解集为
x> ,求m的取值范围.
例1 设 x>y ,用“>”或“<”填空:
;
;
;
.
例3 已知关于x的不等式 .
(1)当m=1时,求该不等式的最小整数解;
(2) m取何值时,该不等式有解,并求出解集.
例3 已知关于x的不等式 .
(1)当m=1时,求该不等式的最小整数解;
解:当m=1时,不等式可化为 .
去分母,得 .
去括号,得 .
移项,得 .
合并同类项,得 .
系数化为1,得 .
所以这个不等式的解集为 .
6
这个不等式的解集在数轴上表示,如图.
所以当m=1时,这个不等式的最小整数解为 .
1
2
3
0
-1
例3 已知关于x的不等式 .
(2) m取何值时,该不等式有解,并求出解集.
解:去分母,得 .
去括号,得 .
移项,合并同类项,得 .
这里的 表示的是什么数呢?
正数?负数?还是0呢?
例3 已知关于x的不等式 .
(2) m取何值时,该不等式有解,并求出解集.
移项,合并同类项,得 .
因为不等式有解,
所以 .
当 ,即 时,
当 ,即 时,
不等式的解集为 ;
不等式的解集为 .
小结:1.在数轴上表示不等式的解集,要注意包含画实心圆点,不包含画空心圆圈,细分有如下4种情况:
a
x>a
a
x≥a
a
x≤a
a
x<a
形式 一元一次方程 一元一次不等式
解法步骤 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
小结:2.解一元一次不等式与解一元一次方程的步骤相同,通常有以下几步:
形式 一元一次方程 一元一次不等式
解法步骤 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
解 只有一个解 解集(无数个解)
小结:2.解一元一次不等式与解一元一次方程的步骤相同,通常有以下几步:
例4 3x+m=1的 ,求m的取值范围.
关于x的方程
解为负数
x=… (含有m的代数式),
解为负数如何用数学符号表示?
得到了关于m的不等式.
x<0.
解:移项,得3x=1-m.
例4 3x+m=1的 ,求m的取值范围.
系数化为1,得 .
因为方程的解为负数,
所以 x<0,
即 .
所以 m>1.
所以 m的取值范围是m>1.
关于x的方程
解为负数
小结:
1.一些常见的数学术语:正数、负数、非负数 等能准确“翻译”成数学符号;
2.不等式与方程结合的问题,通常是先解方程,将未知数用含有字母的代数式表示,再利用不等关系建立不等式求解.
六、一元一次不等式组
知识概要
一般地,把两个或两个以上含有同一未知数的一元一次不等式合在一起时,就组成了一个一元一次不等式组.
七、不等式组的解集
不等式组中的几个一元一次不等式解集的公共部分叫做由它们所组成的不等式组的解集.
例5 解不等式组 ,并写出它的所有非负整数解.
解:
解不等式① ,去括号,得 .
移项,合并同类项,得 .
系数化为1,得 .
.
①
②
系数化为1,得x≤1.
≥
解不等式② ,去分母,得 .
≥
移项,合并同类项,得 .
≥
例5 解不等式组 ,并写出它的所有非负整数解.
①
②
所以不等式组的解集为 ≤1.
解:
解不等式① ,得 .
所以它的所有非负整数解为0,1.
解不等式② ,得x≤1.
在数轴上表示不等式①、②的解集,如图.
-2
-1
1
0
-3
小结:
1.不等式组解集的确定方法及表示:
不等式组(a>b) 在数轴上表示两个不等式的解集 不等式组的解集 速记口诀 不等式组解集在数轴上表示
x> a
a
b
a
b
a
b
a
b
x< b
b<x< a
无解(空集)
a
b
a
b
同大取大
同小取小
小大大小中间找
大大小小找不了
小结:
1.不等式组解集的确定方法及表示:
2.求不等式组的特殊解,需要先确定不等式组的解集.
例6 已知关于x的不等式3x-m≤0的正整数解仅有3个,求m的取值范围.
含有m的代数式表示不等式的解集,
正整数解仅有3个,你能确定这3个正整数吗?
它只能是1,2,3.
为x≤ .
1
2
3
0
4
这个解集在数轴上表示,如图:
x≤
正整数解仅有3个,为1,2,3.
例6 已知关于x的不等式3x-m≤0的正整数解仅有3个,求m的取值范围.
1
2
3
0
4
所以3≤ < 4.
所以m的取值范围是9≤ m<12.
解:解不等式3x-m≤0得 .
x≤
这个解集在数轴上表示,如图.
x≤
小结:
1.在解决一元一次不等式(组)的特殊解的问题时,通常是先求出不等式(组)的解集,然后再考虑特殊解;
例5 解不等式组 ,并写出它的所有非负整数解.
≥
小结:
2.如果不等式中含有字母,通常是先利用含有字母的代数式表示出不等式的解集,再结合给定的解集或特殊解建立方程或不等式(组)来确定字母的值或取值范围.
例6 已知关于x的不等式3x-m≤0的正整数解仅有3个,求m的取值范围.
例7 关于x的不等式组 的解集为 ,求a,b的值.
解不等式①得 .
①
②
∴ , .
你能用含有a,b的代数式分别表示两个不等式的解集吗?
解不等式②得 .
结合给定的不等式组的解集,你能确定 , 与0,2之间的关系吗?
例7 关于x的不等式组 的解集为 ,求a,b的值.
解:解不等式①得 .
所以 , .
所以a=2,b=-1.
解不等式②得 .
①
②
因为不等式组的解集为 ,
本课总结:
1.解一元一次不等式与解一元一次方程步骤相同,但解一元一次不等式要注意去分母和系数化1时,所乘(或除以)的数是否是负数,乘(或除以)一个负数要改变不等号的方向;
2.在求不等式(组)的特殊解时,可以借助数轴表示解集,再找特殊解,这样既不易求多,也不易漏求;
本课总结:
4.正确理解“正数”、“负数”、“非负数”等关键词的含义;
5.含有字母系数的不等式(组)的问题通常是先用含有系数的代数式表示解集,再结合给定的其它条件转化为方程或不等式(组)的问题求解.
3.能够在不等式(组)解集的代数表达和数轴表示之间正确转换;
作业
1.如果x>y ,试用不等号连接下列各对式子:
(1) -5x与-5y ;(2) 0.2x与0.5y ;(3) x+2 与y-2 .
2.求 的非负整数解.
≤
3.求不等式组 的解集.
≤
初一年级 数学
一元一次不等式和一元一次不等式组复习(第一课时)
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
不等式
去分母
一元一次不等式
解法
性质
概念
不等式的解集
不等式
一元一次不等式组
不等式应用
解一元一次不等式
去括号
移项
合并同类项
系数化为1
解一元一次不等式组
本章知识结构图
方程
一元一次方程
类比
类比
不等式组的解集
解一元一次方程
类比
一、不等式的概念
知识概要
用不等号表示不等关系的式子叫做不等式.
表示不等关系的符号:>、<、≥、≤、≠.
表示不等关系的语言:大于、小于、不大于、不少于…
还有一些常见的数学术语:正数、负数、非负数.
一、不等式的概念
知识概要
用不等号表示不等关系的式子叫做不等式.
下列各式是不等式的有( )
① ;
② ;
③ ;
④ ;
⑤ ;
①,②,④,⑥
⑥ .
≤
二、不等式的基本性质
知识概要
1.不等式两边都加上(或减去)同一个数或同一个整式,不等号的方向不变;
如果a>b ,那么 a±c>b±c .
2.不等式两边都乘(或除以)同一个正数,不等号的方向不变;
如果a>b ,c>0,那么ac>bc(或 ) .
二、不等式的基本性质
知识概要
3.不等式两边都乘(或除以)同一个负数,不等号的方向改变.
如果a>b , c<0 ,那么ac<bc (或 ) .
例1 设 x>y ,用“>”或“<”填空:
;
;
;
.
例1 设 x>y ,用“>”或“<”填空:
;
>
不等式的基本性质1
例1 设 x>y ,用“>”或“<”填空:
>
;
;
>
不等式的基本性质2
例1 设 x>y ,用“>”或“<”填空:
>
>
;
;
;
再根据不等式的基本性质1
先根据不等式的基本性质2
>
例1 设 x>y ,用“>”或“<”填空:
>
>
;
;
;
再根据不等式的基本性质2
先根据不等式的基本性质1
>
例1 设 x>y ,用“>”或“<”填空:
>
>
>
;
;
;
.
<
再根据不等式的基本性质1
先根据不等式的基本性质3
例1 设 x>y ,用“>”或“<”填空:
>
<
>
>
思考:若x>y ,则 .
当a=0时, a2=0,
当a表示正数,即a>0时,
当a表示负数,即a<0时,
;
;
;
.
a2>0,
a2x> a2y;
a2>0,
a2x> a2y .
a2x= a2y;
≥
三、不等式的解
知识概要
使不等式成立的未知数的值叫做不等式的解.
四、不等式的解集
一个不等式的所有解组成的集合叫做这个不等式的解集.
五、一元一次不等式
知识概要
只含有一个未知数,并且未知数的最高次数是1,系数不等于0,这样的不等式叫做一元一次不等式.
解不等式就是求不等式解集的过程.就是利用不等式的基本性质将不等式化为x>a或x
对比: (1-m )x 2
x
不等式的基本性质3 ,
不等号的方向发生了改变,由此你想到了什么?
<
>
这里1-m<0 .
例2 已知关于x的不等式(1-m )x<2的解集为x> ,求m的取值范围.
解:因为不等号的方向发生了改变,
利用的是不
等式的基本性质3,
所以不等式两边同时除以(1-m ),
这里1-m<0 , m>1 .
所以m的取值范围是m>1 .
不等式的基本性质的应用一般有两种:
1.已知变形方式,依据不等式的基本性质确定不等号的方向;
2.已知变形结果,依据不等号的方向确定不等式的基本性质
例2 关于x的不等式(1-m )x<2的解集为
x> ,求m的取值范围.
例1 设 x>y ,用“>”或“<”填空:
;
;
;
.
例3 已知关于x的不等式 .
(1)当m=1时,求该不等式的最小整数解;
(2) m取何值时,该不等式有解,并求出解集.
例3 已知关于x的不等式 .
(1)当m=1时,求该不等式的最小整数解;
解:当m=1时,不等式可化为 .
去分母,得 .
去括号,得 .
移项,得 .
合并同类项,得 .
系数化为1,得 .
所以这个不等式的解集为 .
6
这个不等式的解集在数轴上表示,如图.
所以当m=1时,这个不等式的最小整数解为 .
1
2
3
0
-1
例3 已知关于x的不等式 .
(2) m取何值时,该不等式有解,并求出解集.
解:去分母,得 .
去括号,得 .
移项,合并同类项,得 .
这里的 表示的是什么数呢?
正数?负数?还是0呢?
例3 已知关于x的不等式 .
(2) m取何值时,该不等式有解,并求出解集.
移项,合并同类项,得 .
因为不等式有解,
所以 .
当 ,即 时,
当 ,即 时,
不等式的解集为 ;
不等式的解集为 .
小结:1.在数轴上表示不等式的解集,要注意包含画实心圆点,不包含画空心圆圈,细分有如下4种情况:
a
x>a
a
x≥a
a
x≤a
a
x<a
形式 一元一次方程 一元一次不等式
解法步骤 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
小结:2.解一元一次不等式与解一元一次方程的步骤相同,通常有以下几步:
形式 一元一次方程 一元一次不等式
解法步骤 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1 ①去分母
②去括号
③移项
④合并同类项
⑤系数化为1
解 只有一个解 解集(无数个解)
小结:2.解一元一次不等式与解一元一次方程的步骤相同,通常有以下几步:
例4 3x+m=1的 ,求m的取值范围.
关于x的方程
解为负数
x=… (含有m的代数式),
解为负数如何用数学符号表示?
得到了关于m的不等式.
x<0.
解:移项,得3x=1-m.
例4 3x+m=1的 ,求m的取值范围.
系数化为1,得 .
因为方程的解为负数,
所以 x<0,
即 .
所以 m>1.
所以 m的取值范围是m>1.
关于x的方程
解为负数
小结:
1.一些常见的数学术语:正数、负数、非负数 等能准确“翻译”成数学符号;
2.不等式与方程结合的问题,通常是先解方程,将未知数用含有字母的代数式表示,再利用不等关系建立不等式求解.
六、一元一次不等式组
知识概要
一般地,把两个或两个以上含有同一未知数的一元一次不等式合在一起时,就组成了一个一元一次不等式组.
七、不等式组的解集
不等式组中的几个一元一次不等式解集的公共部分叫做由它们所组成的不等式组的解集.
例5 解不等式组 ,并写出它的所有非负整数解.
解:
解不等式① ,去括号,得 .
移项,合并同类项,得 .
系数化为1,得 .
.
①
②
系数化为1,得x≤1.
≥
解不等式② ,去分母,得 .
≥
移项,合并同类项,得 .
≥
例5 解不等式组 ,并写出它的所有非负整数解.
①
②
所以不等式组的解集为 ≤1.
解:
解不等式① ,得 .
所以它的所有非负整数解为0,1.
解不等式② ,得x≤1.
在数轴上表示不等式①、②的解集,如图.
-2
-1
1
0
-3
小结:
1.不等式组解集的确定方法及表示:
不等式组(a>b) 在数轴上表示两个不等式的解集 不等式组的解集 速记口诀 不等式组解集在数轴上表示
x> a
a
b
a
b
a
b
a
b
x< b
b<x< a
无解(空集)
a
b
a
b
同大取大
同小取小
小大大小中间找
大大小小找不了
小结:
1.不等式组解集的确定方法及表示:
2.求不等式组的特殊解,需要先确定不等式组的解集.
例6 已知关于x的不等式3x-m≤0的正整数解仅有3个,求m的取值范围.
含有m的代数式表示不等式的解集,
正整数解仅有3个,你能确定这3个正整数吗?
它只能是1,2,3.
为x≤ .
1
2
3
0
4
这个解集在数轴上表示,如图:
x≤
正整数解仅有3个,为1,2,3.
例6 已知关于x的不等式3x-m≤0的正整数解仅有3个,求m的取值范围.
1
2
3
0
4
所以3≤ < 4.
所以m的取值范围是9≤ m<12.
解:解不等式3x-m≤0得 .
x≤
这个解集在数轴上表示,如图.
x≤
小结:
1.在解决一元一次不等式(组)的特殊解的问题时,通常是先求出不等式(组)的解集,然后再考虑特殊解;
例5 解不等式组 ,并写出它的所有非负整数解.
≥
小结:
2.如果不等式中含有字母,通常是先利用含有字母的代数式表示出不等式的解集,再结合给定的解集或特殊解建立方程或不等式(组)来确定字母的值或取值范围.
例6 已知关于x的不等式3x-m≤0的正整数解仅有3个,求m的取值范围.
例7 关于x的不等式组 的解集为 ,求a,b的值.
解不等式①得 .
①
②
∴ , .
你能用含有a,b的代数式分别表示两个不等式的解集吗?
解不等式②得 .
结合给定的不等式组的解集,你能确定 , 与0,2之间的关系吗?
例7 关于x的不等式组 的解集为 ,求a,b的值.
解:解不等式①得 .
所以 , .
所以a=2,b=-1.
解不等式②得 .
①
②
因为不等式组的解集为 ,
本课总结:
1.解一元一次不等式与解一元一次方程步骤相同,但解一元一次不等式要注意去分母和系数化1时,所乘(或除以)的数是否是负数,乘(或除以)一个负数要改变不等号的方向;
2.在求不等式(组)的特殊解时,可以借助数轴表示解集,再找特殊解,这样既不易求多,也不易漏求;
本课总结:
4.正确理解“正数”、“负数”、“非负数”等关键词的含义;
5.含有字母系数的不等式(组)的问题通常是先用含有系数的代数式表示解集,再结合给定的其它条件转化为方程或不等式(组)的问题求解.
3.能够在不等式(组)解集的代数表达和数轴表示之间正确转换;
作业
1.如果x>y ,试用不等号连接下列各对式子:
(1) -5x与-5y ;(2) 0.2x与0.5y ;(3) x+2 与y-2 .
2.求 的非负整数解.
≤
3.求不等式组 的解集.
≤
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
