人教版六年级数学下册 4-3比例的应用 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版六年级数学下册 4-3比例的应用 同步拓展讲与练+奥数培优(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 762.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 10:49:53 | ||
图片预览



文档简介
比例的应用、比例尺、图形的缩放
知识引入:
比例的应用:
(一)正比例的应用:
例题1:小红的身高1.6米,她的影长2.5米,如果同一时间、同一地点测得一棵树的影子长4米,这棵树有多高?
算数法: 比例法:
知识精讲1:
用正比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成正比例。
(2)找出两组相对应的数,并设出未知数,列出比例。
(3)解比例。
(4)检验并写出答语。
(二)反比例的应用:
例题2:一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
算数法: 比例法:
知识精讲2:
用反比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成反比例关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。
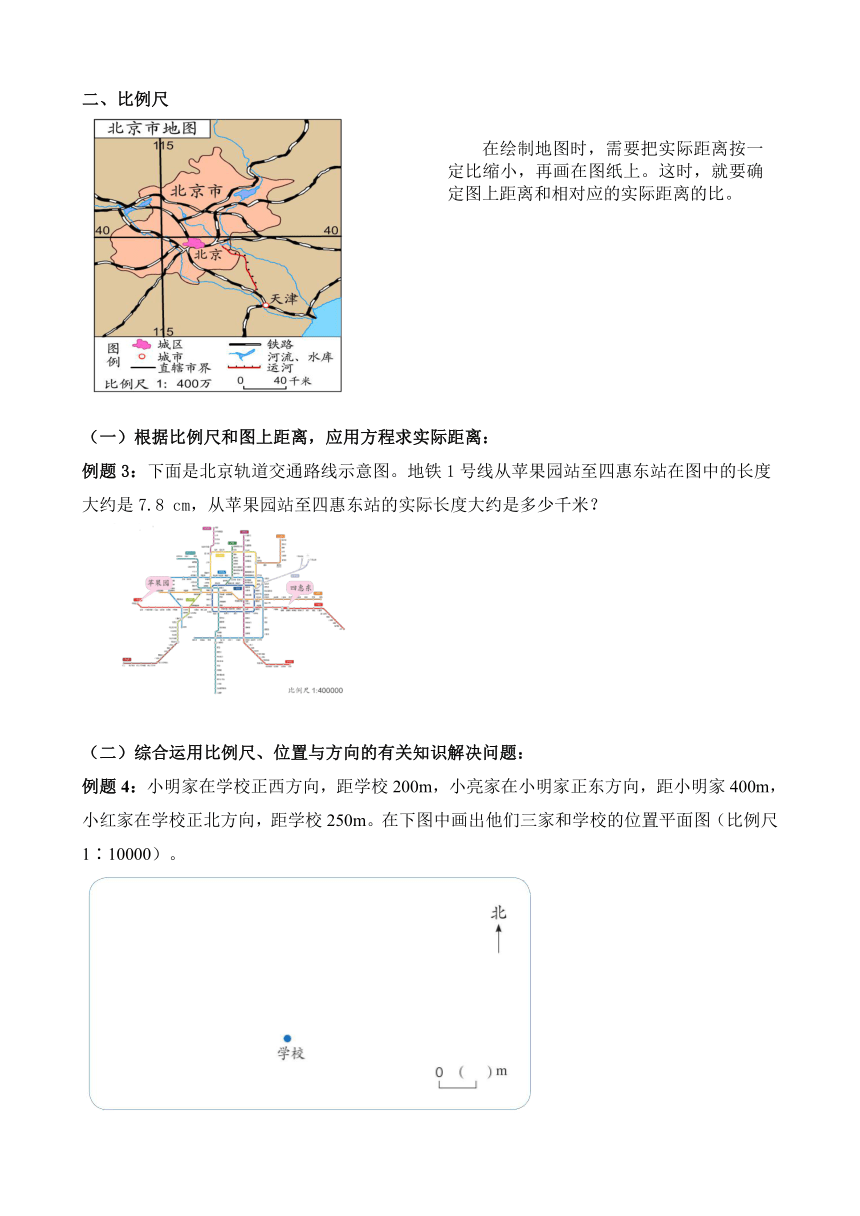
二、比例尺
(一)根据比例尺和图上距离,应用方程求实际距离:
例题3:下面是北京轨道交通路线示意图。地铁1号线从苹果园站至四惠东站在图中的长度大约是7.8 cm,从苹果园站至四惠东站的实际长度大约是多少千米?
(二)综合运用比例尺、位置与方向的有关知识解决问题:
例题4:小明家在学校正西方向,距学校200m,小亮家在小明家正东方向,距小明家400m,小红家在学校正北方向,距学校250m。在下图中画出他们三家和学校的位置平面图(比例尺1∶10000)。
知识精讲3:比例尺
1.比例尺的意义:一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
2.比例尺的分类:
比例尺按表现形式分为数值比例尺和线段比例尺;
按作用的不同分为缩小比例尺和放大比例尺。
3.已知比例尺和图上距离,求实际距离的常用方法:
(1)可以根据“图上距离∶实际距离=比例尺”列比例解答。
(2)利用“实际距离=图上距离÷比例尺”直接列式计算。
4.应用比例尺画平面图时:先要根据比例尺和实际距离求出图上距离,再根据图上距离画出
相应的位置,并标明比例尺。
三、图形的缩放:
例5:按2∶1画出下面三个图形放大后的图形。
知识精讲4:图形的缩放
1.图形的放大与缩小是生活中常见的现象,把一个图形放大或缩小后所得的图形与原来的图形相比,形状相同,大小不同。
2.在方格纸上画出按一定的比将图形放大或缩小后的图形的方法:
一看:看原图各边占几格;
二算:计算按一定的比把图形放大或缩小后得到的新图形的各边占几格。
三画:按计算后得到的新图形的边长画出新图形。
巩固练习:
1.填空。
(1)食堂买3桶油用780元,照这样计算,买8桶油用多少元??
①本题中( ?? ?)是一定的,(?? )和( ??)成(? )比例关系。
②如果设买8桶油用x元,那么列出比例式是(?? ??????)。?
某种型号钢珠,3个重22.5克。现有一些这种型号的钢珠,共945克,一共有多少个?
? ①本题中( ? )是一定的,( ? ??)和(? ???? )成(?? ???)比例关系。?
②如果设一共有x个,那么比例式是( )。
(3)比例尺表示一幅图的图上距离和实际距离的( ),所以, 比例尺没有单位。
(4)可以用关系式( )∶( )=比例尺或者比例尺=( ) 。
(5)在比例尺是1∶8000000的地图上,图上1厘米表示实际( )厘米,也就是( )千米。
(6)改写成数值比例尺是( )。
(7)比例尺是10∶1的平面图上,表示( )是( )的10倍。
(8)图上距离∶ ( )=比例尺。实际距离=( )÷( )。
(9)学校平面图的比例尺是1 ∶ 30000,从教学楼到图书馆的图上距离为2.2厘米,教学楼到图书馆的实际距离是( )厘米,即( )米。
(10)一幅地图的比例尺为 ,那么图上距离为3cm时,实际距离为( )个35km,是( )km。
(11)根据图上距离∶实际距离=比例尺,可得图上距离=( )。
(12)A、B两地相距34km,在比例尺为1∶500000的地图上, A、B两地间的距离是( )。
(13)一个零件实际长度是3.1mm,将它画在比例尺为15∶1的图纸上,图上零件长( )mm。
(14)一幅地图,图上2 cm表示实际距离100 km,这幅地图的比例尺是( )。
(15)中国目前最高的建筑物是位于广州的广州塔。在比例尺是1:5000的图纸上,量得它的
高度为12 cm,广州塔的实际高度是( )。
2.解决问题。
(1)车队向灾区运送一批救灾物资,去时每小时行60千米,6.5小时到达灾区。回来时每小时行78千米,多长时间能够返回出发地点?
(2)学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?
(3)小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔,要用多少钱?
(4)陈大妈家上月用了8t水,水费是28元。田奶奶家上用了10t水。应交多少元水费?
(5)在一幅地图上,量得甲、乙两地之间的距离是10cm,而甲、乙两地之间的实际距离是300km,这幅地图的比例尺是多少?
(6)一幅北京地图的比例尺是1∶5000000,而一幅天津地图比例尺表示为 ,这两幅地图的比例尺一样大吗?
(7)在比例尺是1∶12000000的地图上,量得从甲地到乙地的距离为1.7cm,甲、乙两地的实际距离为多少千米?
(8)在一张比例尺为12∶1的图纸上,量得一个手表零件的长度为6cm,则它的实际长度为多少厘米?
9、学校要建一个长80m、宽60m的长方形操场,请画出操场的平面图。(比例尺1∶2000)
10、兰州到乌鲁木齐的铁路线大约长1900km。地图上两地之间的长度是多少厘米?
奥数思维拓展:变化的比例尺
1.渗透两种数学思想:变中有不变思想、符号化思想。
2.学习一种思维方法:转换法。
思维提升:
[例]在比例尺是1:40000的一幅地图上,量得甲、乙两地之间的距离是3cm,现在改用1:50000的比例尺重新绘制,甲、乙两地之间的距离应该画几厘米?
[分析]
此类问题在生活中经常遇到,因为绘制条件的不同,所以选用的比例尺不同。不管比例尺怎样变化,实际距离是不变的。因此解决此类问题时找到这一突破口,根据已知的比例尺先求出3cm的实际距离,再根据新的比例尺与甲、乙两个城市间的实际距离,求出图上距离。
[解答]
3÷ =120000(cm)
120000× =2.4(cm)
答:甲、乙两地之间的距离应该画2.4厘米。
[技巧]无论比例尺怎样变化,只需抓住实际距离不变求解即可。
举一反三:
1、在一幅比例尺是1:10000的一幅地图上,量得李明家到学校的距离是15cm。在另一幅比例尺是1:30000的地图上,李明家到学校的图上距离是多少?
2、在比例尺是1:3000000的一幅地图上,量得甲、乙两城之间的距离是2.4cm。在另一幅地图上量得甲、乙两城之间的距离是3.6cm,求另一幅地图的比例尺。
在绘制地图时,需要把实际距离按一定比缩小,再画在图纸上。这时,就要确定图上距离和相对应的实际距离的比。
知识引入:
比例的应用:
(一)正比例的应用:
例题1:小红的身高1.6米,她的影长2.5米,如果同一时间、同一地点测得一棵树的影子长4米,这棵树有多高?
算数法: 比例法:
知识精讲1:
用正比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成正比例。
(2)找出两组相对应的数,并设出未知数,列出比例。
(3)解比例。
(4)检验并写出答语。
(二)反比例的应用:
例题2:一个办公楼原来平均每天照明用电100千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来5天的用电量现在可以用多少天?
算数法: 比例法:
知识精讲2:
用反比例知识解决问题的步骤:
(1)根据不变量判断题中哪两种相关联的量成反比例关系。
(2)找出两组相对应的数,并设出未知数,列出方程。
(3)解方程。
(4)检验并写出答语。
二、比例尺
(一)根据比例尺和图上距离,应用方程求实际距离:
例题3:下面是北京轨道交通路线示意图。地铁1号线从苹果园站至四惠东站在图中的长度大约是7.8 cm,从苹果园站至四惠东站的实际长度大约是多少千米?
(二)综合运用比例尺、位置与方向的有关知识解决问题:
例题4:小明家在学校正西方向,距学校200m,小亮家在小明家正东方向,距小明家400m,小红家在学校正北方向,距学校250m。在下图中画出他们三家和学校的位置平面图(比例尺1∶10000)。
知识精讲3:比例尺
1.比例尺的意义:一幅图的图上距离和实际距离的比,叫做这幅图的比例尺。
2.比例尺的分类:
比例尺按表现形式分为数值比例尺和线段比例尺;
按作用的不同分为缩小比例尺和放大比例尺。
3.已知比例尺和图上距离,求实际距离的常用方法:
(1)可以根据“图上距离∶实际距离=比例尺”列比例解答。
(2)利用“实际距离=图上距离÷比例尺”直接列式计算。
4.应用比例尺画平面图时:先要根据比例尺和实际距离求出图上距离,再根据图上距离画出
相应的位置,并标明比例尺。
三、图形的缩放:
例5:按2∶1画出下面三个图形放大后的图形。
知识精讲4:图形的缩放
1.图形的放大与缩小是生活中常见的现象,把一个图形放大或缩小后所得的图形与原来的图形相比,形状相同,大小不同。
2.在方格纸上画出按一定的比将图形放大或缩小后的图形的方法:
一看:看原图各边占几格;
二算:计算按一定的比把图形放大或缩小后得到的新图形的各边占几格。
三画:按计算后得到的新图形的边长画出新图形。
巩固练习:
1.填空。
(1)食堂买3桶油用780元,照这样计算,买8桶油用多少元??
①本题中( ?? ?)是一定的,(?? )和( ??)成(? )比例关系。
②如果设买8桶油用x元,那么列出比例式是(?? ??????)。?
某种型号钢珠,3个重22.5克。现有一些这种型号的钢珠,共945克,一共有多少个?
? ①本题中( ? )是一定的,( ? ??)和(? ???? )成(?? ???)比例关系。?
②如果设一共有x个,那么比例式是( )。
(3)比例尺表示一幅图的图上距离和实际距离的( ),所以, 比例尺没有单位。
(4)可以用关系式( )∶( )=比例尺或者比例尺=( ) 。
(5)在比例尺是1∶8000000的地图上,图上1厘米表示实际( )厘米,也就是( )千米。
(6)改写成数值比例尺是( )。
(7)比例尺是10∶1的平面图上,表示( )是( )的10倍。
(8)图上距离∶ ( )=比例尺。实际距离=( )÷( )。
(9)学校平面图的比例尺是1 ∶ 30000,从教学楼到图书馆的图上距离为2.2厘米,教学楼到图书馆的实际距离是( )厘米,即( )米。
(10)一幅地图的比例尺为 ,那么图上距离为3cm时,实际距离为( )个35km,是( )km。
(11)根据图上距离∶实际距离=比例尺,可得图上距离=( )。
(12)A、B两地相距34km,在比例尺为1∶500000的地图上, A、B两地间的距离是( )。
(13)一个零件实际长度是3.1mm,将它画在比例尺为15∶1的图纸上,图上零件长( )mm。
(14)一幅地图,图上2 cm表示实际距离100 km,这幅地图的比例尺是( )。
(15)中国目前最高的建筑物是位于广州的广州塔。在比例尺是1:5000的图纸上,量得它的
高度为12 cm,广州塔的实际高度是( )。
2.解决问题。
(1)车队向灾区运送一批救灾物资,去时每小时行60千米,6.5小时到达灾区。回来时每小时行78千米,多长时间能够返回出发地点?
(2)学校小商店有两种圆珠笔,小明带的钱刚好可以买4支单价是1.5元的,如果他只买单价是2元的,可以买多少支?
(3)小明买4支圆珠笔用了6元,小刚想买3支同样的圆珠笔,要用多少钱?
(4)陈大妈家上月用了8t水,水费是28元。田奶奶家上用了10t水。应交多少元水费?
(5)在一幅地图上,量得甲、乙两地之间的距离是10cm,而甲、乙两地之间的实际距离是300km,这幅地图的比例尺是多少?
(6)一幅北京地图的比例尺是1∶5000000,而一幅天津地图比例尺表示为 ,这两幅地图的比例尺一样大吗?
(7)在比例尺是1∶12000000的地图上,量得从甲地到乙地的距离为1.7cm,甲、乙两地的实际距离为多少千米?
(8)在一张比例尺为12∶1的图纸上,量得一个手表零件的长度为6cm,则它的实际长度为多少厘米?
9、学校要建一个长80m、宽60m的长方形操场,请画出操场的平面图。(比例尺1∶2000)
10、兰州到乌鲁木齐的铁路线大约长1900km。地图上两地之间的长度是多少厘米?
奥数思维拓展:变化的比例尺
1.渗透两种数学思想:变中有不变思想、符号化思想。
2.学习一种思维方法:转换法。
思维提升:
[例]在比例尺是1:40000的一幅地图上,量得甲、乙两地之间的距离是3cm,现在改用1:50000的比例尺重新绘制,甲、乙两地之间的距离应该画几厘米?
[分析]
此类问题在生活中经常遇到,因为绘制条件的不同,所以选用的比例尺不同。不管比例尺怎样变化,实际距离是不变的。因此解决此类问题时找到这一突破口,根据已知的比例尺先求出3cm的实际距离,再根据新的比例尺与甲、乙两个城市间的实际距离,求出图上距离。
[解答]
3÷ =120000(cm)
120000× =2.4(cm)
答:甲、乙两地之间的距离应该画2.4厘米。
[技巧]无论比例尺怎样变化,只需抓住实际距离不变求解即可。
举一反三:
1、在一幅比例尺是1:10000的一幅地图上,量得李明家到学校的距离是15cm。在另一幅比例尺是1:30000的地图上,李明家到学校的图上距离是多少?
2、在比例尺是1:3000000的一幅地图上,量得甲、乙两城之间的距离是2.4cm。在另一幅地图上量得甲、乙两城之间的距离是3.6cm,求另一幅地图的比例尺。
在绘制地图时,需要把实际距离按一定比缩小,再画在图纸上。这时,就要确定图上距离和相对应的实际距离的比。
