人教版六年级数学下册 数的认识 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版六年级数学下册 数的认识 同步拓展讲与练+奥数培优(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 459.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 10:52:12 | ||
图片预览



文档简介
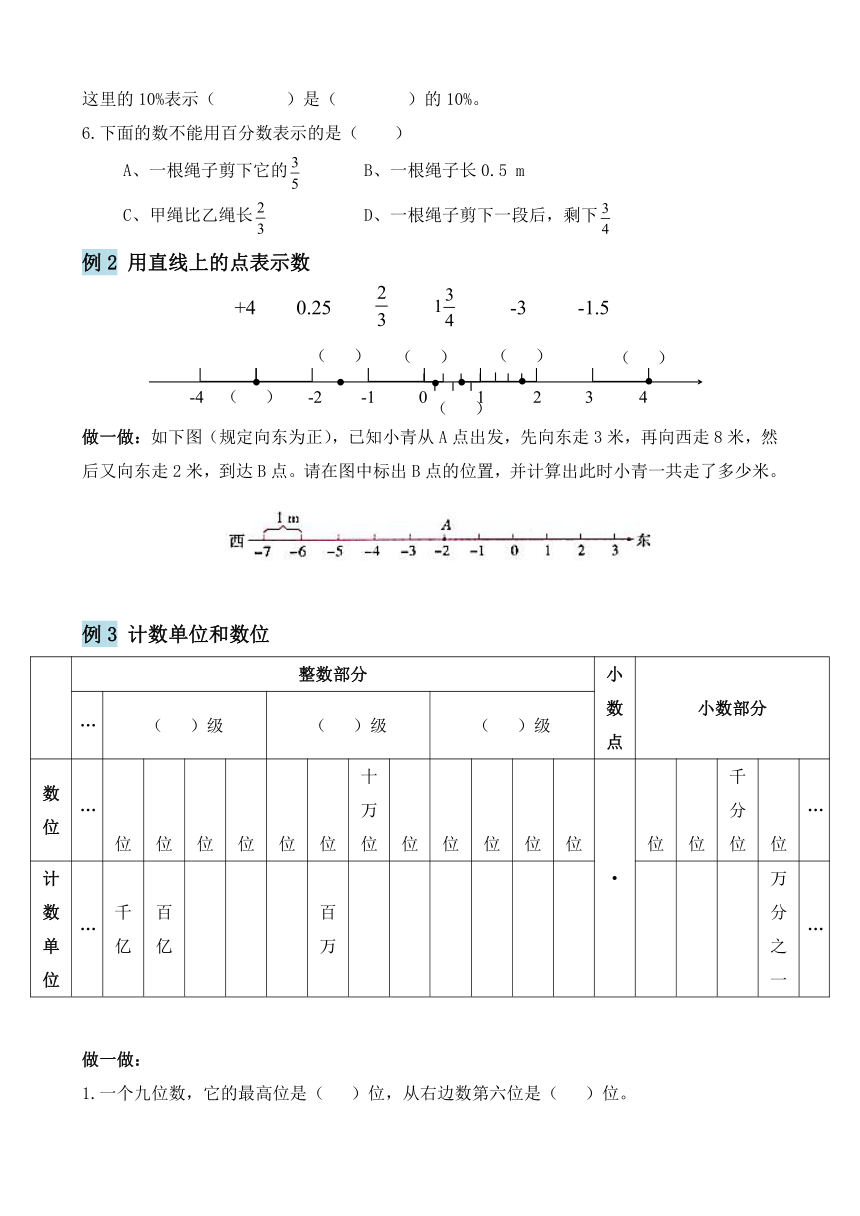
数的认识(数的意义、性质、读写法、大小比较)
例1 数的分类
正整数
整数 零
数 负整数
正分数(正小数)
分数(小数)
负分数(负小数)
做一做:
1. -3.5 8 6098 -76 0.43 0 π
整数: ; 小数: ;
分数: ; 自然数: ;
正数: ; 负数: ;
( )既不是正数,也不是负数。
2.把1 m长的铁丝平均分成7份,每份占全长的( ),其中的5份是( )m;把5 m长的铁丝平均分成7份,每份占全长的( ),其中的1份是( )m。
3.要使是假分数,是真分数,应该是( )。
4.据调查,我国每年浪费的食物总量折合粮食约500亿千克,相当于全国粮食总产量的10%,这里的10%表示( )是( )的10%。
6.下面的数不能用百分数表示的是( )
A、一根绳子剪下它的 B、一根绳子长0.5 m
C、甲绳比乙绳长 D、一根绳子剪下一段后,剩下
例2 用直线上的点表示数
做一做:如下图(规定向东为正),已知小青从A点出发,先向东走3米,再向西走8米,然后又向东走2米,到达B点。请在图中标出B点的位置,并计算出此时小青一共走了多少米。
例3 计数单位和数位
整数部分 小 数 点 小数部分
… ( )级 ( )级 ( )级
数 位 … 位 位 位 位 位 位 十 万 位 位 位 位 位 位 · 位 位 千 分 位 位 …
计 数 单 位 … 千 亿 百 亿 百 万 万 分 之 一 …
做一做:
1.一个九位数,它的最高位是( )位,从右边数第六位是( )位。
2. 9.27是由( )个一,( )个十分之一和( )个百分之一组成的,它是一个( )位小数。
6.3的计数单位是( ),6.30的计数单位是( )。
4.下面各数中“9”表示的含义是什么?
92 0.59 903.8
例4 分数的基本性质
分数的分子和分母 ,分数的大小不变。
做一做:
1.
2.的分子加上5,要使分数的大小不变,分母应( )。
3.一个分数,分子扩大到原来的4倍,分母扩大到原来的3倍,得到的结果是,这个分数是( )。
4.一个分数约分成最简分数是,约分前分子、分母的和是48,约分前的分数是( )。
A. B. C.
例5 小数的性质
在小数的 添上0或者去掉0,小数的大小不变。
做一做:
1.把5.4改写成计数单位是千分之一的数是( )。
2.在0.5末尾填上2个0,它的大小( ),但它的计数单位由( )变为( )。
例6 小数点位置移动引起小数大小变化的规律
小数点向右移动一位,相当于把原数乘 ,小数就扩大到原数的 倍;
移动两位,相当于把原数乘 ,小数就扩大到原数的 倍;
移动三位,相当于把原数乘 ,小数就扩大到原数的 倍。
小数点向左移动一位,相当于把原数除以 ,小数就缩小到原数的 ;
移动两位,相当于把原数除以 ,小数就缩小到原数的 ;
移动三位,相当于把原数除以 ,小数就缩小到原数的 。
做一做:
1.36的小数点先向左移动两位,再向右移动一位,这个数将( )。
2.去掉0.38的小数点,使它变成整数,原数就增加( )倍,在38后面填上“%”,原数就减少( )%。
例7 数的读写法
读法:203003000 写法: 三十亿五千零八十万
12.073 二十点三零六
一又九分之三
35% 百分之七十
+36 正五
-2.09 负二分之一
做一做:
1.十三亿七千零五十三万六千八百七十五 写作:
2.下面的数读出两个零的是( )。
A.505050 B.555000 C.500505 D.500055
例8 数的改写
直接改写:“=”连接,移动小数点,后面写“万”或“亿”字。
改写成近似数:“≈”连接,四舍五入法省略万位或亿位后面的尾数,后面写“万”或“亿”字。
2.假分数→整数或带分数
方法:分子÷分母
分子是分母整数倍:假分数→整数 分子÷分母=商 →商就是这个整数,没有分母
分子不是分母整数倍:假分数→带分数 分子÷分母=商……余数
3.整数或带分数→假分数
整数(0除外)→假分数:用指定的分母做分母,分母×整数 → 分子。
带分数→假分数:分母不变,整数×分母+分子 → 分子。
分数、小数、百分数之间的互化
做一做:
1.一个数由8个百万,6个十万,7个千,4个十,6个和5个0.01组成,这个数是( ),四舍五入到万位约是( )。
2.2013年年末中国城镇人口数为73111万人,乡村人口数为62961万人,城乡总人口数是( )万人,改写成用“亿”作单位的数是( )亿人,省略亿位后面的尾数约是( )亿人。
3.一个自然数四舍五入到万位后是50000,这个自然数最大是( ),最小是( );一个两位小数精确到十分位后是20.0,这个两位小数最大是( ),最小是( )。
4.下面各式中“□”里可以填哪些数字?写在后面的横线上。
7□00<7300 57□000≈58万
36□0000000≈36亿
例9 数的大小比较
整数:
先看位数→
小数:
先看整数部分→
分数:
分母相同,分子大的分数大;
分子相同,分母小的分数大;
分子分母都不同,先通分再比较大小
带分数&带分数 : 整数部分大的分数大,整数部分相同,比较分数部分
带分数&假分数 : 带分数→假分数,或假分数→带分数,再比较大小
假分数>真分数 带分数>真分数
做一做:
1.把 π 3.14 用“<”连接起来。
2.把 0.33 0.34 33.3% 按从大到小的顺序排列。
3.,下面( )组中的5个数分别填入□中都合适。
A.8、9、10、11、12 B.9、10、11、12、13
C.10、11、12、13、14 D.11、12、13、14、15
综合训练
下列说法正确的是( )。
A.0是正数 B.0是负数 C.0是整数
2.把0.25的小数点向右移动两位后,再向左移动一位,这个数就( )。
A.扩大到原来的100倍 B.缩小到原来的
C.扩大到原来的10倍 D.缩小到原来的
3.、、、、按从小到大的顺序排列,第三个数是( )。
如果,那么□内可以填的自然数有( )个。
最简分数满足,当它的分母最小时( )
一个三位小数用“四舍五入”法取近似值是7.68,这个三位小数最大是( ),最小是( )。
一个六位数,个位上的数字是5,十万位上的数字是9,任意相邻三个数字的和都是20,这个六位数是( )。
8.乙数比甲数多29.7,乙数的小数点向左移动两位后正好等于甲数,甲数与乙数的和是多少?
9.甲乙两数的和是162.8,乙数的小数点向右移动一位就等于甲数,求甲、乙两数各是多少。
10.甲乙两数的和是3.63,把甲数的小数点向左移动一位就和乙数相等,甲数是( )。
11.一个四位数,在它的某一位数字前面点上一个小数点,再和这个四位数相加,得数是2000.81,这个四位数是多少?
12.一个三位数,十位上是0,个位与百位上的数字之和是9,如果把这个三位数的个位数字与百位数字对调,则得到的新三位数比原来的三位数大693,求原来的三位数。
13.如果将6放在一个两位数的最右端,所得的三位数比原来的两位数大294。原来的两位数是多少?
①把原来的两位数看成x,把6放在两位数的最右端,则这个三位数是
10x+( )。
②根据两个数的差列方程,即10x+( )-x=( ),求得x=( )。
③如果把4放在一个两位数的最右端,所得的三位数比原来的两位数大652,
那么原来的两位数是( )。
14.一个分数的分子与分母的和是90,化简后是,这个分数原来是多少?
15.大于而小于,且分子是6的最简真分数有几个?分别是多少?
自然数
数
正数
负数
零
正整数
正分数(正小数)
负整数
负分数(负小数)
+4 0.25 -3 -1.5
-4 ( ) -2 -1 0 1 2 3 4
( )
( )
( )
( )
( )
1.
(小数部分末尾的0划掉)
要把小数保留到哪一位,就看这一位后面一位上的数,再按“四舍五入”法省略。
整数部分
分子
分母不变
3.
位数不同,位数多的数大
位数相同,从最高位比起,相同数位上的数大的那个数就大
整数部分不同,整数部分大的那个数就大
整数部分相同,十分位上的数大的那个数就大;
十分位相同,百分位上的数大的那个数就大……
真分数&真分数
假分数&假分数
