人教版数学七年级下册9.1.2 不等式的性质课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级下册9.1.2 不等式的性质课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 289.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 19:15:01 | ||
图片预览






文档简介
(共22张PPT)
人教版 七年级数学下册
第9章不等式与不等式组
9.1.2 不等式的性质
新知导入
爸爸你今年32岁,我才9岁,你的年龄比我大,但是再过24年,我就比你大了。
新知导入
等式和不等式只有一字之差,不等式是否也具有同样的性质呢?
等式的性质
等式的基本性质1: 在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2: 在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc 或 (c≠0),
新知讲解
观察:用“<”或“>”填空,并找一找其中的规律。
(2) –1<3 -1+3____3+3
-1-3____3-3
6>4 6+2____4+2
6-2____4-2
>
>
<
<
发现:当不等式两边加上或减去同一个数时,
不等号的方向________
不变
不等式基本性质1
新知讲解
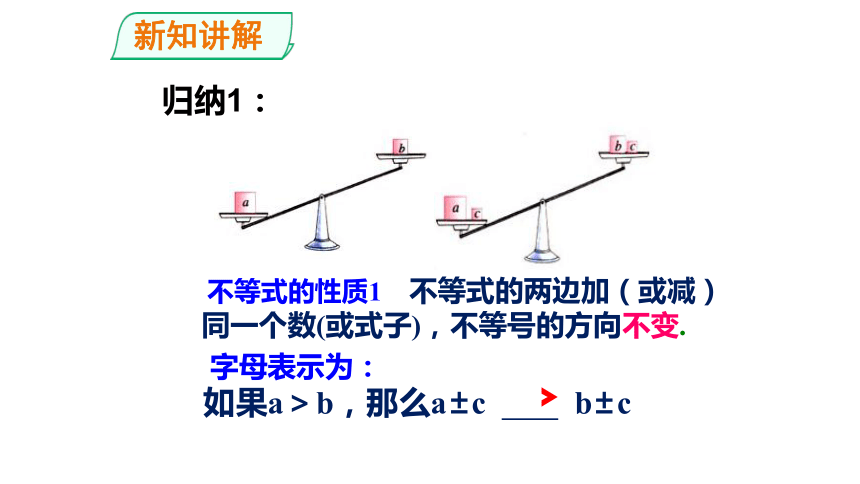
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c b±c
字母表示为:
﹥
归纳1:
发现: 当不等式的两边都乘以(或除以)同一个正数时,不等号的方向______ .
新知讲解
(3) 6>2 6×5____2×5
6 ÷ 5____ 2 ÷ 5
(4) –2<3 (-2)×6____3×6
(-2)÷ 6 ____3 ÷ 6
>
>
<
不变
观察:用“<”或“>”填空,并找一找其中的规律.
<
不等式基本性质2
新知讲解
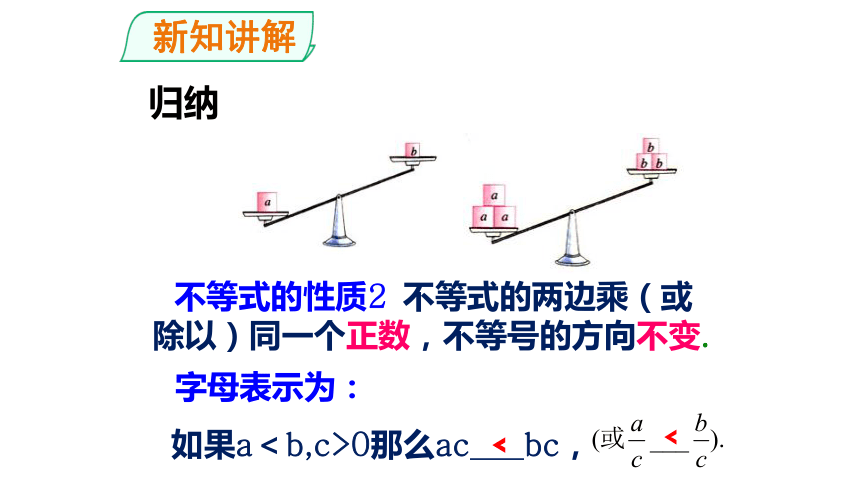
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a<b,c>0那么ac bc,
字母表示为:
﹤
﹤
归纳
新知讲解
(5) 6>2 6 x(- 2) ____ 2 x(- 2)
6 ÷(-2) ____ 2 ÷(-2)
(6) –2<4 (-2) x(- 2) ____ 4 x(-2)
(-2) ÷(-2)____4 ÷(-2)
发现:当不等式的两边都乘以(或 除以)同一个负数时,不等号的方向________.
>
<
>
改变
观察:用“<”或“>”填空,并找一找其中的规律.
<
不等式基本性质3
新知讲解
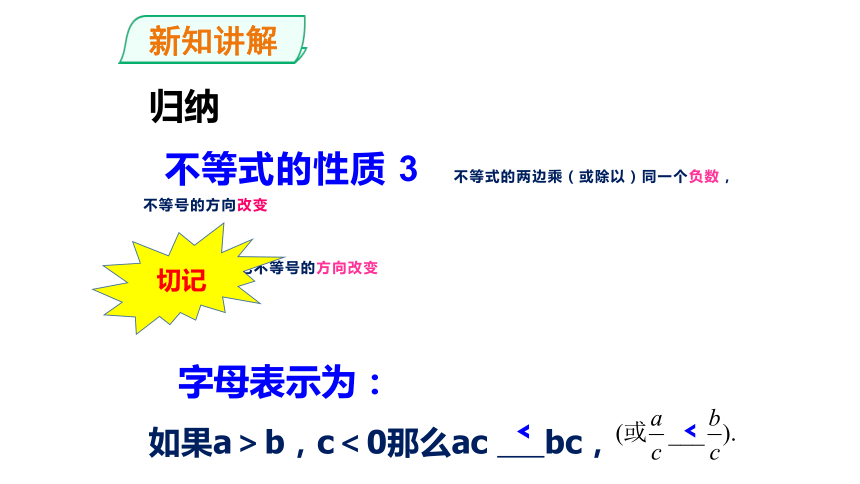
不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
必须把不等号的方向改变
字母表示为:
如果a>b,c<0那么ac bc,
﹤
﹤
归纳
切记
巩固练习
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 3____b - 3;
(2) a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
巩固练习
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; ?(2)a-1 _____-1;
(3)3a______0; (4)- ______0;
(5)a2 _____0; (6)a3 ______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
巩固练习
3.判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2, 那么a>b。
×
×
例题讲解
例1、利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1;
(3) ﹥50; (4)-4x﹥3.
这个不等式的解集在数轴上的表示如图所示:
解:(1)根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
0
33
例题讲解
例1、利用不等式的性质解下列不等式:
(2)3x<2x+1;(3) ﹥50; (4)-4x﹥3.
解:(2)x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
(3) x﹥75
这个不等式的解集在数轴上的表示如图所示:
0
75
(4)x﹤-
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
例题讲解
例2、某长方体的容器长5cm,宽3cm,高10cm。容器内原有水的高度为3cm, 现准备向它继续注水。用V(单位:cm3 )表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即
V+3×5×3≤3×5×10
解得 V≤105
又由于新注入水的体积不能是负数,因此,
V的取值范围是
V≥0并且V≤105
在数轴上表示V的取值范围如图
在表示0和105的点上画实心圆点,表示取值范围包括这两个数
0
105
新知讲解
解未知数为x的不等式
化为x>a或x<a的形式
目标
方法:不等式基本性质1~3
1、解不等式的思路:
2、解不等式的注意事项:
②在数轴上表示解集应注意的问题: 方向、空心或实心
①在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
巩固练习
4、若a>b,则 ( )
(A)a>-b (B)a<-b
(C)-2a>-2b (D)-2a<-2b
解:不等式的两边都乘以-2,不等号的方向改变.
D
巩固练习
(1)5x < 200 ;
(3)x - 4 ≥ 2(x+2)
5、把下列不等式的解集表示在数轴上.
(2)
(4)
答案: (1)
(2)
(3)
(4)
-4
-2
-1
0
-8
1
2
3
0
-1
38
39
37
40
41
42
36
35
34
x<40
-11
-10
-12
-9
-8
-7
-13
-14
-15
-3
-5
-6
-7
-2
-1
0
-8
-3
-5
-6
-7
-2
-1
0
-8
x>-7
x≤-8
x>
1
2
3
0
-1
-11
-10
-12
-9
-8
-7
-13
-14
-15
-3
-5
-6
-7
-2
-1
0
-8
-3
-5
-6
-7
-2
-1
0
-8
巩固练习
6、某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打( )
(A)6折 (B)7折 (C)8折 (D)9折
解:设打x折,由题意得1 200×10x%-800≥
800×5%,解得x≥7,即最多可打7折 .
B
7、有下列说法:
(1)若a<b,则-a>-b;
(2)若xy<0,则x<0,y<0;
(3)若x<0,y<0,则xy<0;
(4)若a<b,则2a<a+b;
(5)若a<b,则
其中正确的说法有( )
A、2个 B、3个 C、4个 D、5个
(6)若 ,则x>y.
巩固练习
B
课堂总结
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
通过本课时的学习,需要我们掌握:
利用不等式的性质将不等式化为:x>a 或 x<a的形式
作业布置
教材120页3、4、5题
人教版 七年级数学下册
第9章不等式与不等式组
9.1.2 不等式的性质
新知导入
爸爸你今年32岁,我才9岁,你的年龄比我大,但是再过24年,我就比你大了。
新知导入
等式和不等式只有一字之差,不等式是否也具有同样的性质呢?
等式的性质
等式的基本性质1: 在等式两边都加上(或减去)同一个数或整式,结果仍相等.
如果a=b,那么a±c=b±c
等式的基本性质2: 在等式两边都乘以或除以同一个数(除数不为0),结果仍相等.
如果a=b,那么ac=bc 或 (c≠0),
新知讲解
观察:用“<”或“>”填空,并找一找其中的规律。
(2) –1<3 -1+3____3+3
-1-3____3-3
6>4 6+2____4+2
6-2____4-2
>
>
<
<
发现:当不等式两边加上或减去同一个数时,
不等号的方向________
不变
不等式基本性质1
新知讲解
不等式的性质1 不等式的两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c b±c
字母表示为:
﹥
归纳1:
发现: 当不等式的两边都乘以(或除以)同一个正数时,不等号的方向______ .
新知讲解
(3) 6>2 6×5____2×5
6 ÷ 5____ 2 ÷ 5
(4) –2<3 (-2)×6____3×6
(-2)÷ 6 ____3 ÷ 6
>
>
<
不变
观察:用“<”或“>”填空,并找一找其中的规律.
<
不等式基本性质2
新知讲解
不等式的性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
如果a<b,c>0那么ac bc,
字母表示为:
﹤
﹤
归纳
新知讲解
(5) 6>2 6 x(- 2) ____ 2 x(- 2)
6 ÷(-2) ____ 2 ÷(-2)
(6) –2<4 (-2) x(- 2) ____ 4 x(-2)
(-2) ÷(-2)____4 ÷(-2)
发现:当不等式的两边都乘以(或 除以)同一个负数时,不等号的方向________.
>
<
>
改变
观察:用“<”或“>”填空,并找一找其中的规律.
<
不等式基本性质3
新知讲解
不等式的性质 3 不等式的两边乘(或除以)同一个负数,不等号的方向改变
必须把不等号的方向改变
字母表示为:
如果a>b,c<0那么ac bc,
﹤
﹤
归纳
切记
巩固练习
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
(1) a - 3____b - 3;
(2) a÷3____b÷3
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
>
>
>
>
>
<
不等式的性质1
不等式的性质2
不等式的性质2
不等式的性质3
不等式的性质1,2
不等式的性质2
巩固练习
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; ?(2)a-1 _____-1;
(3)3a______0; (4)- ______0;
(5)a2 _____0; (6)a3 ______0;
(7)a-1_____0;??(8)|a|______0.
<
<
<
>
<
>
<
>
巩固练习
3.判断正误:
(1)如果a>b,那么ac>bc。
(2)如果a>b,那么ac2>bc2。
(3)如果ac2>bc2, 那么a>b。
×
×
例题讲解
例1、利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1;
(3) ﹥50; (4)-4x﹥3.
这个不等式的解集在数轴上的表示如图所示:
解:(1)根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7
x﹥33
0
33
例题讲解
例1、利用不等式的性质解下列不等式:
(2)3x<2x+1;(3) ﹥50; (4)-4x﹥3.
解:(2)x﹤1
这个不等式的解集在数轴上的表示如图所示:
0
1
(3) x﹥75
这个不等式的解集在数轴上的表示如图所示:
0
75
(4)x﹤-
这个不等式的解集在数轴上的表示如图所示:
-
4
3
0
例题讲解
例2、某长方体的容器长5cm,宽3cm,高10cm。容器内原有水的高度为3cm, 现准备向它继续注水。用V(单位:cm3 )表示新注入水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积的和不能
超过容器的容积,即
V+3×5×3≤3×5×10
解得 V≤105
又由于新注入水的体积不能是负数,因此,
V的取值范围是
V≥0并且V≤105
在数轴上表示V的取值范围如图
在表示0和105的点上画实心圆点,表示取值范围包括这两个数
0
105
新知讲解
解未知数为x的不等式
化为x>a或x<a的形式
目标
方法:不等式基本性质1~3
1、解不等式的思路:
2、解不等式的注意事项:
②在数轴上表示解集应注意的问题: 方向、空心或实心
①在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向.
巩固练习
4、若a>b,则 ( )
(A)a>-b (B)a<-b
(C)-2a>-2b (D)-2a<-2b
解:不等式的两边都乘以-2,不等号的方向改变.
D
巩固练习
(1)5x < 200 ;
(3)x - 4 ≥ 2(x+2)
5、把下列不等式的解集表示在数轴上.
(2)
(4)
答案: (1)
(2)
(3)
(4)
-4
-2
-1
0
-8
1
2
3
0
-1
38
39
37
40
41
42
36
35
34
x<40
-11
-10
-12
-9
-8
-7
-13
-14
-15
-3
-5
-6
-7
-2
-1
0
-8
-3
-5
-6
-7
-2
-1
0
-8
x>-7
x≤-8
x>
1
2
3
0
-1
-11
-10
-12
-9
-8
-7
-13
-14
-15
-3
-5
-6
-7
-2
-1
0
-8
-3
-5
-6
-7
-2
-1
0
-8
巩固练习
6、某种商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多可打( )
(A)6折 (B)7折 (C)8折 (D)9折
解:设打x折,由题意得1 200×10x%-800≥
800×5%,解得x≥7,即最多可打7折 .
B
7、有下列说法:
(1)若a<b,则-a>-b;
(2)若xy<0,则x<0,y<0;
(3)若x<0,y<0,则xy<0;
(4)若a<b,则2a<a+b;
(5)若a<b,则
其中正确的说法有( )
A、2个 B、3个 C、4个 D、5个
(6)若 ,则x>y.
巩固练习
B
课堂总结
不等式的性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的性质2 不等式两边乘(或除以)同一个正数,不等号的方向不变.
不等式的性质3 不等式两边乘(或除以)同一个负数,不等号的方向改变.
通过本课时的学习,需要我们掌握:
利用不等式的性质将不等式化为:x>a 或 x<a的形式
作业布置
教材120页3、4、5题
