人教版数学七年级下册课件:9.2 一元一次不等式(第2课时)(共29张PPT)
文档属性
| 名称 | 人教版数学七年级下册课件:9.2 一元一次不等式(第2课时)(共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 176.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览








文档简介
(共29张PPT)
人教版 七年级数学下册
第9章 不等式与不等式组
9.2 一元一次不等式(第2课时)
一元一次不等式的应用
学习目标
1.能分析出简单实际问题中的不等关系,列出一元一次不等式求解.
2.体会数学建模的思想.
【1】下列式子中,一元一次不等式有( )
①3x-1≥4
② 2+3x>6
③ 3- <5
④
⑤
⑥ x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
一元一次不等式的定义和性质
√
√
×
√
√
×
√
复习旧知
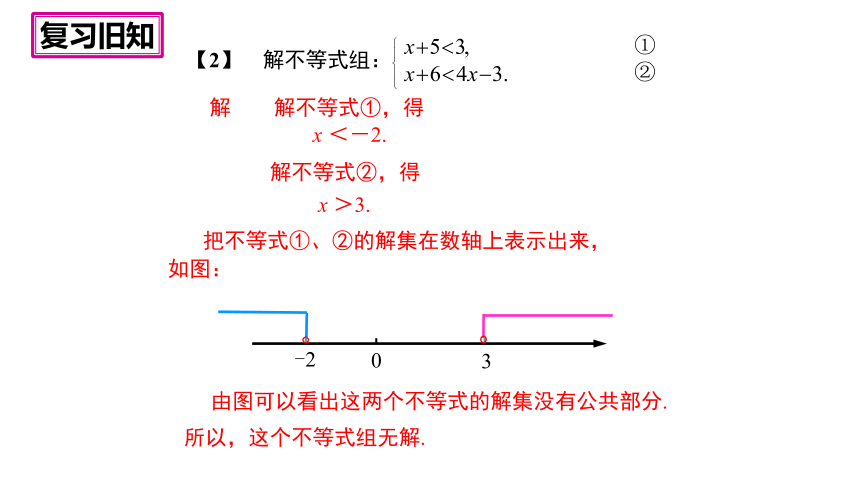
【2】 解不等式组:
解 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
复习旧知
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题1 你是如何理解题意的呢?
问题探究
问题2 此实际问题中的不等关系是什么?
问题探究
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
不等关系是:
问题探究
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题3 设x表示明年增加的空气质量良好
的天数,则明年空气质量是良好的天数是
多少?
问题探究
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
设x表示明年增加的空气质量良好的
天数,则明年空气质量是良好的天数
是:
问题探究
问题探究
问题4 你能列出不等式并解出来吗?
解:设明年比去年空气质量良好的天数增加了x天.
问题5 你能给出一个合理化的答案吗?
答:明年要比去年空气质量良好的天数
至少增加37,才能使这一年空气质量良
好的天数超过全年天数的70%.
问题探究
巩固练习
1.某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化, 准备提前2天完成修路任务,以后几天 内平均每天至少要修路多少?
解:设以后几天平均每天至少要修路x米.
巩固练习
答:以后几天平均每天至少要修路 0.8米.
例3 甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题1 你是如何理解题意的呢?
问题探究
问题探究
问题2 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题探究
问题3 你能清楚直观地表示上述问题吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题4 你能看出在哪个商场花费少呢?
购物款 甲商场 乙商场 比较
一样
乙
?
问题探究
问题5 如果累计购物超过100元,在哪家商场花费少呢?
分析:三种情况进行讨论
(1)什么情况下,到甲商场购物花费少?
(2) 什么情况下,到乙商场购物花费少?
(3)什么情况下,两商场花费一样?
问题探究
(1)若在甲超市花费少,则
.
得 .
问题探究
(2)若在乙超市花费少,则
.
得 .
问题探究
(3)若在两超市花费一样,则
.
得 .
问题探究
问题6 你能综合上面分析给出一个合理化的消费方案吗?
答:购物不超过50元和刚好是150元时,
在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
问题探究
1.利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数,列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
实际问题的解答
检验
数学建模
归纳提高
2.某次知识竞赛共有20道题,每一道题 答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?
巩固练习
解:设至少要答对 道题.
巩固练习
答:至少要答对13道题.
【归纳拓展】当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
巩固练习
1.列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
总结归纳
2.一元一次不等式的实际问题中最关键是哪一步?
3.不等式的实际问题与方程的实际问题有什么相同和不同之处?
总结归纳
布置作业
教科书 习题9.2 第5、6、7、8、9题
人教版 七年级数学下册
第9章 不等式与不等式组
9.2 一元一次不等式(第2课时)
一元一次不等式的应用
学习目标
1.能分析出简单实际问题中的不等关系,列出一元一次不等式求解.
2.体会数学建模的思想.
【1】下列式子中,一元一次不等式有( )
①3x-1≥4
② 2+3x>6
③ 3- <5
④
⑤
⑥ x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
一元一次不等式的定义和性质
√
√
×
√
√
×
√
复习旧知
【2】 解不等式组:
解 解不等式①,得
x <-2.
解不等式②,得
x >3.
①
②
把不等式①、②的解集在数轴上表示出来,
如图:
由图可以看出这两个不等式的解集没有公共部分.
所以,这个不等式组无解.
0
-2
3
复习旧知
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题1 你是如何理解题意的呢?
问题探究
问题2 此实际问题中的不等关系是什么?
问题探究
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
不等关系是:
问题探究
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
问题3 设x表示明年增加的空气质量良好
的天数,则明年空气质量是良好的天数是
多少?
问题探究
例2 去年某市空气质量良好(二级以上)的天数与全年天数(365)之比达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良好的天数要比去年至少增加多少?
设x表示明年增加的空气质量良好的
天数,则明年空气质量是良好的天数
是:
问题探究
问题探究
问题4 你能列出不等式并解出来吗?
解:设明年比去年空气质量良好的天数增加了x天.
问题5 你能给出一个合理化的答案吗?
答:明年要比去年空气质量良好的天数
至少增加37,才能使这一年空气质量良
好的天数超过全年天数的70%.
问题探究
巩固练习
1.某工程队计划在10天内修路6 km.施工前2天修完1.2 km后,计划发生变化, 准备提前2天完成修路任务,以后几天 内平均每天至少要修路多少?
解:设以后几天平均每天至少要修路x米.
巩固练习
答:以后几天平均每天至少要修路 0.8米.
例3 甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题1 你是如何理解题意的呢?
问题探究
问题探究
问题2 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题探究
问题3 你能清楚直观地表示上述问题吗?
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?
问题4 你能看出在哪个商场花费少呢?
购物款 甲商场 乙商场 比较
一样
乙
?
问题探究
问题5 如果累计购物超过100元,在哪家商场花费少呢?
分析:三种情况进行讨论
(1)什么情况下,到甲商场购物花费少?
(2) 什么情况下,到乙商场购物花费少?
(3)什么情况下,两商场花费一样?
问题探究
(1)若在甲超市花费少,则
.
得 .
问题探究
(2)若在乙超市花费少,则
.
得 .
问题探究
(3)若在两超市花费一样,则
.
得 .
问题探究
问题6 你能综合上面分析给出一个合理化的消费方案吗?
答:购物不超过50元和刚好是150元时,
在两家商场购物没有区别;超过50元而不到150元时在乙商场购物花费少;超过150元后,在甲商场购物花费少.
问题探究
1.利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数,列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
实际问题的解答
检验
数学建模
归纳提高
2.某次知识竞赛共有20道题,每一道题 答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?
巩固练习
解:设至少要答对 道题.
巩固练习
答:至少要答对13道题.
【归纳拓展】当应用题中出现以下的关键词,如大,小,多,少,不小于,不大于,至少,至多等,应属列不等式(组)来解决的问题,而不能列方程(组)来解.
巩固练习
1.列一元一次不等式组解实际问题的一般步骤:
(1)审题;
(2)设未知数,找不等量关系;
(3)根据不等关系列不等式组;
(4)解不等式组;
(5)检验并作答.
总结归纳
2.一元一次不等式的实际问题中最关键是哪一步?
3.不等式的实际问题与方程的实际问题有什么相同和不同之处?
总结归纳
布置作业
教科书 习题9.2 第5、6、7、8、9题
