人教版六年级数学下册 圆柱的认识和表面积 同步拓展讲与练+奥数培优(无答案)
文档属性
| 名称 | 人教版六年级数学下册 圆柱的认识和表面积 同步拓展讲与练+奥数培优(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 601.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 14:16:31 | ||
图片预览

文档简介
圆柱的认识和表面积
知识引入:
一、圆柱的认识
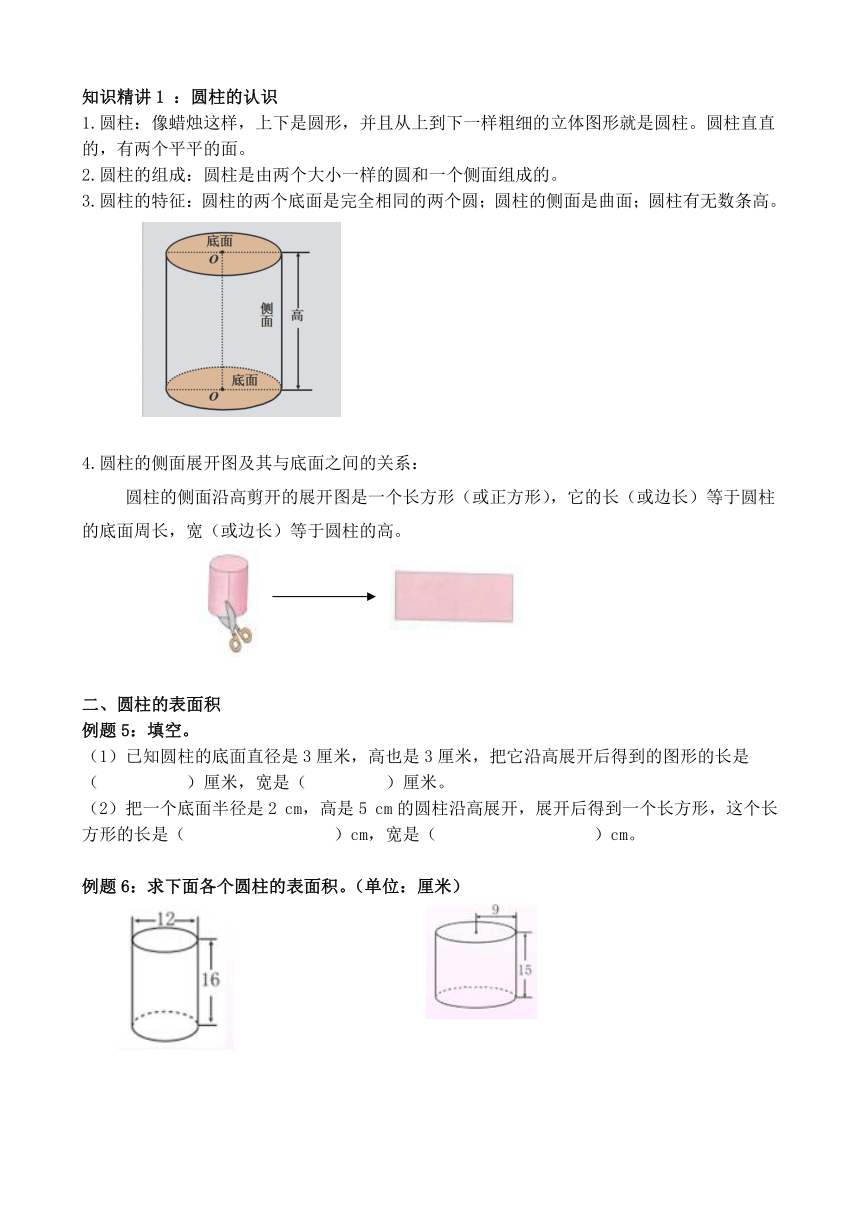
例题1:填空。
(1)圆柱的上、下两个面叫做( ),它们是两个 ( )的圆。
(2)圆柱有一个曲面,叫做( ),圆柱的两底面之间的距离叫做( ),圆柱的高有( )条。
(3)如图,以边AB所在的直线为轴旋转一周,形成一个( ),
它的底面半径是( )cm、高是( )cm,底面面积是
( )cm。
例题2:判断正误。判断正误。(对的在括号里打“√”,错的打“×”。)
(1)圆柱的高只有一条。( )
(2)圆柱的侧面是一个曲面。( )
(3)圆柱的两个底面的直径相等。( )
例题3:连一连,填一填 。
(1)折一折,想一想,连一连。
(2)已知圆柱的底面直径是3厘米,高也是3厘米,把它沿高将侧面展开后得到的长方形的长是( )厘米,宽是( )厘米。
例题4:选择。
(1)将圆柱侧面展开后不可能得到( )。
A.平行四边形 B.正方形 C.梯形 D.长方形
(2)把一个圆柱沿高将侧面展开后得到一个正方形,圆柱底面半径为5cm,圆柱高为 ( )。
A.5 cm B.10 cm C.31.4 cm D.78.5 cm
(3)圆柱的底面直径为10厘米,高为5厘米,若切成2个小圆 柱,每个切面是( ),若沿直径切为2个半圆柱,每个切面是( )。
A.圆形 B.长方形 C.半圆形 D.正方形
知识精讲1 :圆柱的认识
1.圆柱:像蜡烛这样,上下是圆形,并且从上到下一样粗细的立体图形就是圆柱。圆柱直直的,有两个平平的面。
2.圆柱的组成:圆柱是由两个大小一样的圆和一个侧面组成的。
3.圆柱的特征:圆柱的两个底面是完全相同的两个圆;圆柱的侧面是曲面;圆柱有无数条高。
4.圆柱的侧面展开图及其与底面之间的关系:
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),它的长(或边长)等于圆柱的底面周长,宽(或边长)等于圆柱的高。
圆柱的表面积
例题5:填空。
(1)已知圆柱的底面直径是3厘米,高也是3厘米,把它沿高展开后得到的图形的长是( )厘米,宽是( )厘米。
(2)把一个底面半径是2 cm,高是5 cm的圆柱沿高展开,展开后得到一个长方形,这个长方形的长是(?? ? ? ?)cm,宽是(??? ?? )cm。
例题6:求下面各个圆柱的表面积。(单位:厘米)
例题7:用一张长15厘米,宽8厘米的长方形纸围一个圆柱,这个圆柱的侧面积是多少平方厘米?
例题8:选择填空。
A.做圆柱形通风管需多少铁皮 B.圆柱形水池的占地面积
C.压路机滚筒转动一周压路的面积 D.做圆柱形无盖水桶需要多少铁皮
E.做圆柱形油桶需要多少铁皮 F.做圆柱形井盖需要多大面积的水泥板
(1)求两个底面的面积与侧面积的和:( )
(2)求一个底面的面积与侧面积的和:( )
(3)求侧面积:( )
(4)求底面积:( )
例题9:解决问题。
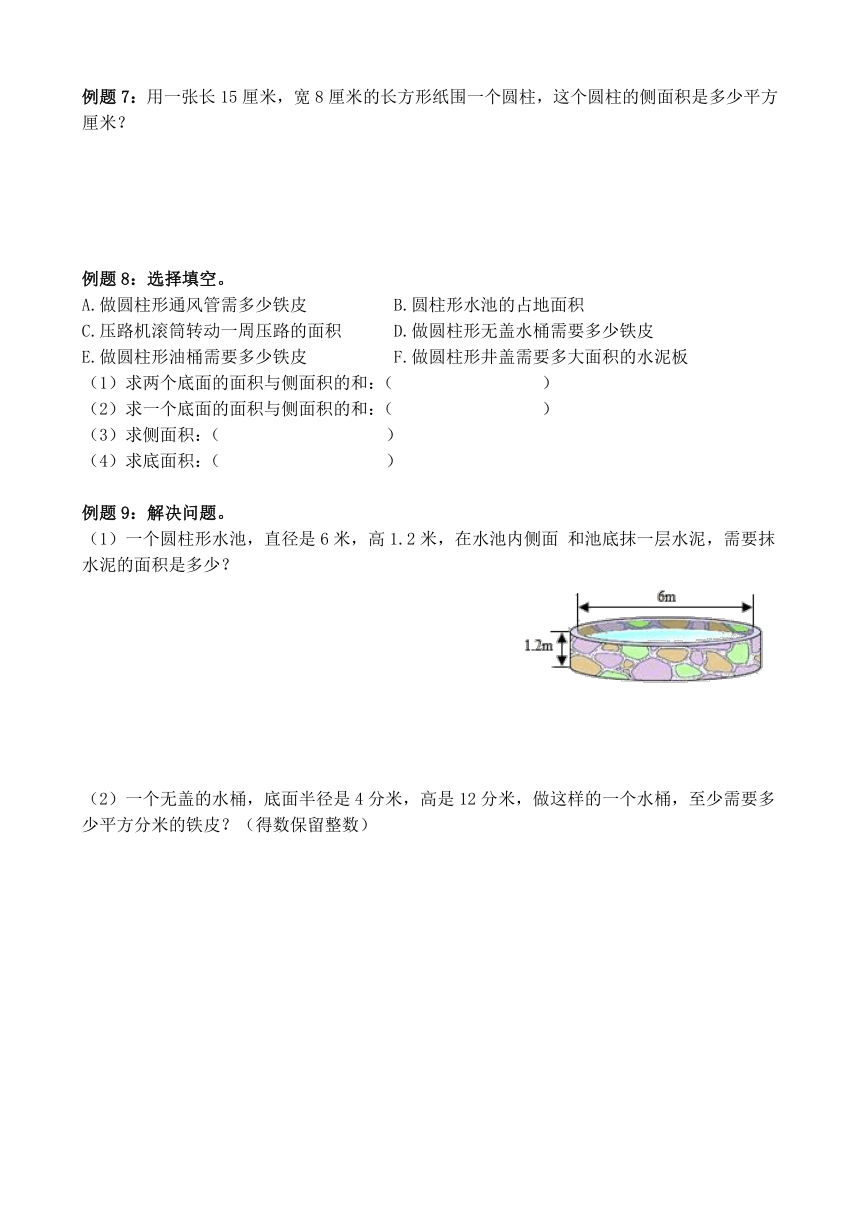
(1)一个圆柱形水池,直径是6米,高1.2米,在水池内侧面 和池底抹一层水泥,需要抹水泥的面积是多少?
(2)一个无盖的水桶,底面半径是4分米,高是12分米,做这样的一个水桶,至少需要多少平方分米的铁皮?(得数保留整数)
知识精讲2:圆柱的表面积
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
S表 = S侧 + 2S圆
已知底面周长C和圆柱的高h,S侧=
已知底面半径r和圆柱的高h,S侧=
已知底面直径d和圆柱的高h,S侧=
S表 = S侧 + 2S圆
= + +
= +
= + +
巩固练习:
1.用铁皮制作一节圆柱形通风管,它的长是60 cm,底面直径是10 cm,至少需要多少平方
厘米铁皮?
2.小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要多少彩纸?
3.某种饮料罐的形状为圆柱形,底面直径为6cm,高为12cm,将24罐这种饮料按如图
所示的方式放入箱内,这个箱子的长、宽、高至少是多少厘米?
4.圆柱的高不变,底面半径扩大到原来的3倍,它的侧面积将扩大到原来的( )。
A、3倍 B、6倍 C、9倍
5.甲乙两人分别利用一张长20 cm,宽18 cm的纸用两种不同的方法围成一个圆筒
(接头处不重叠),则围成的圆筒( )。
A、高一定相等 B、侧面积一定相等 C、侧面积和高都不相等
6.制作10节底面直径是2 dm,长是2 m的圆柱形铁皮通风管,至少需要铁皮( )dm2。
A、125.6 B、1.256 C、1256
7.一根圆柱形木料,底面直径是20 cm,高是1.2 m,如果把它横切或纵切成相同的两部分,分开后两块木料的表面积的和是多少?
8.计算右边圆柱的侧面积。(单位:dm)
9.计算右面圆柱的表面积。(单位:cm)
10.一个圆柱的底面周长是94.2 cm,高是25 cm,求它的表面积。
11.一个圆柱的侧面展开图是边长为9.42 cm的正方形,求这个圆柱的表面积。
12.一台压路机的前轮是圆柱形,轮宽2 m,直径1.2 m,前轮转动一周,压路的
面积是多少平方米?
奥数思维拓展:圆柱的表面积问题
1.渗透两种数学思想:化归思想、数形结合思想
2.学习两种思维方法:图示法、推理法。
思维提升:
[例]一块长方形的玻璃板,利用图中涂色部分刚好能做成一个圆柱形带盖水桶(接头处忽略不计)。这个水桶的表面积是多少?
[分析]
求水桶的表面积就要知道水桶的底面半径(或直径)和高。
涂色长方形的长=圆柱的底面周长,大长方形的长=圆柱的底面周长+底面直径,宽为圆柱的高,是底面直径的2倍。
[解答]
底面直径:16.65÷(3.14+1)=4(分米)
水桶的高:4×2=8(分米)
水桶的表面积:3.14×(4÷2)×2+3.14×4×8=125.6(平方分米)
答:这个水桶的表面积是125.6平方分米。
[技巧]解决此类问题的关键是找出圆柱与平面图形之间的联系。
举一反三:
1.如图,有一张长方形铁皮,剪下两个圆及一个长方形,正好可以做成一个圆柱,这个圆柱的底面半径为10cm,那么原来长方形铁皮的面积是多少平方厘米?
2.有一块长方形的铁皮(如图),剪下涂色部分围成一个圆柱,求这个圆柱的表面积。
5
5
15
10
4
知识引入:
一、圆柱的认识
例题1:填空。
(1)圆柱的上、下两个面叫做( ),它们是两个 ( )的圆。
(2)圆柱有一个曲面,叫做( ),圆柱的两底面之间的距离叫做( ),圆柱的高有( )条。
(3)如图,以边AB所在的直线为轴旋转一周,形成一个( ),
它的底面半径是( )cm、高是( )cm,底面面积是
( )cm。
例题2:判断正误。判断正误。(对的在括号里打“√”,错的打“×”。)
(1)圆柱的高只有一条。( )
(2)圆柱的侧面是一个曲面。( )
(3)圆柱的两个底面的直径相等。( )
例题3:连一连,填一填 。
(1)折一折,想一想,连一连。
(2)已知圆柱的底面直径是3厘米,高也是3厘米,把它沿高将侧面展开后得到的长方形的长是( )厘米,宽是( )厘米。
例题4:选择。
(1)将圆柱侧面展开后不可能得到( )。
A.平行四边形 B.正方形 C.梯形 D.长方形
(2)把一个圆柱沿高将侧面展开后得到一个正方形,圆柱底面半径为5cm,圆柱高为 ( )。
A.5 cm B.10 cm C.31.4 cm D.78.5 cm
(3)圆柱的底面直径为10厘米,高为5厘米,若切成2个小圆 柱,每个切面是( ),若沿直径切为2个半圆柱,每个切面是( )。
A.圆形 B.长方形 C.半圆形 D.正方形
知识精讲1 :圆柱的认识
1.圆柱:像蜡烛这样,上下是圆形,并且从上到下一样粗细的立体图形就是圆柱。圆柱直直的,有两个平平的面。
2.圆柱的组成:圆柱是由两个大小一样的圆和一个侧面组成的。
3.圆柱的特征:圆柱的两个底面是完全相同的两个圆;圆柱的侧面是曲面;圆柱有无数条高。
4.圆柱的侧面展开图及其与底面之间的关系:
圆柱的侧面沿高剪开的展开图是一个长方形(或正方形),它的长(或边长)等于圆柱的底面周长,宽(或边长)等于圆柱的高。
圆柱的表面积
例题5:填空。
(1)已知圆柱的底面直径是3厘米,高也是3厘米,把它沿高展开后得到的图形的长是( )厘米,宽是( )厘米。
(2)把一个底面半径是2 cm,高是5 cm的圆柱沿高展开,展开后得到一个长方形,这个长方形的长是(?? ? ? ?)cm,宽是(??? ?? )cm。
例题6:求下面各个圆柱的表面积。(单位:厘米)
例题7:用一张长15厘米,宽8厘米的长方形纸围一个圆柱,这个圆柱的侧面积是多少平方厘米?
例题8:选择填空。
A.做圆柱形通风管需多少铁皮 B.圆柱形水池的占地面积
C.压路机滚筒转动一周压路的面积 D.做圆柱形无盖水桶需要多少铁皮
E.做圆柱形油桶需要多少铁皮 F.做圆柱形井盖需要多大面积的水泥板
(1)求两个底面的面积与侧面积的和:( )
(2)求一个底面的面积与侧面积的和:( )
(3)求侧面积:( )
(4)求底面积:( )
例题9:解决问题。
(1)一个圆柱形水池,直径是6米,高1.2米,在水池内侧面 和池底抹一层水泥,需要抹水泥的面积是多少?
(2)一个无盖的水桶,底面半径是4分米,高是12分米,做这样的一个水桶,至少需要多少平方分米的铁皮?(得数保留整数)
知识精讲2:圆柱的表面积
圆柱的表面积 = 圆柱的侧面积 + 两个底面的面积
S表 = S侧 + 2S圆
已知底面周长C和圆柱的高h,S侧=
已知底面半径r和圆柱的高h,S侧=
已知底面直径d和圆柱的高h,S侧=
S表 = S侧 + 2S圆
= + +
= +
= + +
巩固练习:
1.用铁皮制作一节圆柱形通风管,它的长是60 cm,底面直径是10 cm,至少需要多少平方
厘米铁皮?
2.小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要多少彩纸?
3.某种饮料罐的形状为圆柱形,底面直径为6cm,高为12cm,将24罐这种饮料按如图
所示的方式放入箱内,这个箱子的长、宽、高至少是多少厘米?
4.圆柱的高不变,底面半径扩大到原来的3倍,它的侧面积将扩大到原来的( )。
A、3倍 B、6倍 C、9倍
5.甲乙两人分别利用一张长20 cm,宽18 cm的纸用两种不同的方法围成一个圆筒
(接头处不重叠),则围成的圆筒( )。
A、高一定相等 B、侧面积一定相等 C、侧面积和高都不相等
6.制作10节底面直径是2 dm,长是2 m的圆柱形铁皮通风管,至少需要铁皮( )dm2。
A、125.6 B、1.256 C、1256
7.一根圆柱形木料,底面直径是20 cm,高是1.2 m,如果把它横切或纵切成相同的两部分,分开后两块木料的表面积的和是多少?
8.计算右边圆柱的侧面积。(单位:dm)
9.计算右面圆柱的表面积。(单位:cm)
10.一个圆柱的底面周长是94.2 cm,高是25 cm,求它的表面积。
11.一个圆柱的侧面展开图是边长为9.42 cm的正方形,求这个圆柱的表面积。
12.一台压路机的前轮是圆柱形,轮宽2 m,直径1.2 m,前轮转动一周,压路的
面积是多少平方米?
奥数思维拓展:圆柱的表面积问题
1.渗透两种数学思想:化归思想、数形结合思想
2.学习两种思维方法:图示法、推理法。
思维提升:
[例]一块长方形的玻璃板,利用图中涂色部分刚好能做成一个圆柱形带盖水桶(接头处忽略不计)。这个水桶的表面积是多少?
[分析]
求水桶的表面积就要知道水桶的底面半径(或直径)和高。
涂色长方形的长=圆柱的底面周长,大长方形的长=圆柱的底面周长+底面直径,宽为圆柱的高,是底面直径的2倍。
[解答]
底面直径:16.65÷(3.14+1)=4(分米)
水桶的高:4×2=8(分米)
水桶的表面积:3.14×(4÷2)×2+3.14×4×8=125.6(平方分米)
答:这个水桶的表面积是125.6平方分米。
[技巧]解决此类问题的关键是找出圆柱与平面图形之间的联系。
举一反三:
1.如图,有一张长方形铁皮,剪下两个圆及一个长方形,正好可以做成一个圆柱,这个圆柱的底面半径为10cm,那么原来长方形铁皮的面积是多少平方厘米?
2.有一块长方形的铁皮(如图),剪下涂色部分围成一个圆柱,求这个圆柱的表面积。
5
5
15
10
4
