北师大版七年级数学下册 4.1 三角形的三边关系 课件(第2课时 17张ppt)
文档属性
| 名称 | 北师大版七年级数学下册 4.1 三角形的三边关系 课件(第2课时 17张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 15:08:37 | ||
图片预览





文档简介
(共17张PPT)
4.1 认识三角形
第2课时 三角形的三边关系
在我们的生活中几乎随处可见三角形。它简单,有趣,也十分有用。三角形可以帮助我们更好认识周围世界,解决很多的实际问题。
学习目标
1.掌握三角形按边分类的方法,能够判定三角形
是否为特殊三角形;
2.探索并掌握三角形三边之间的关系,运用三角形
三边关系解决有关问题.(重点、难点)
讲授新课
一、三角形按边分类
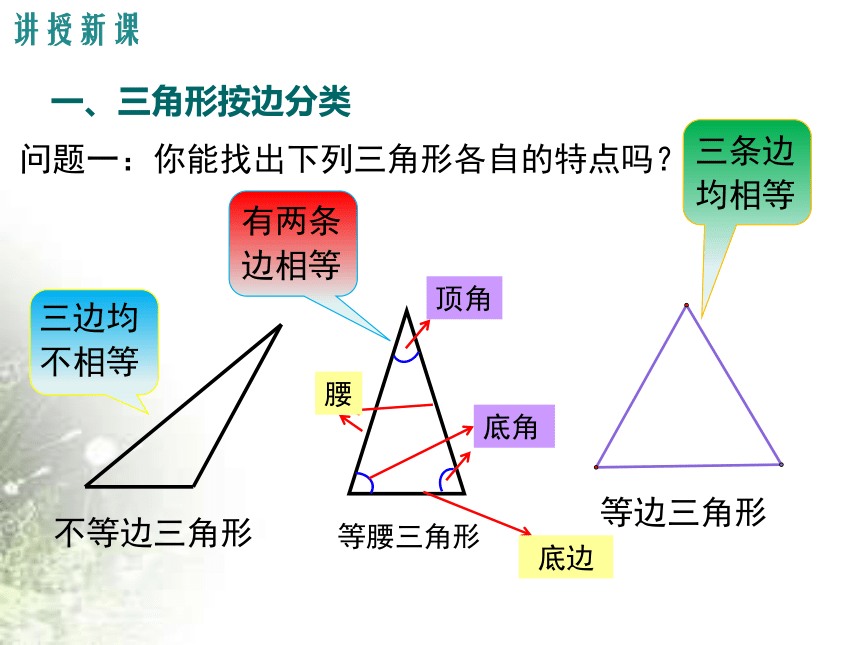
问题一:你能找出下列三角形各自的特点吗?
三边均不相等
不等边三角形
有两条边相等
等腰三角形
等边三角形
三条边均相等
腰
底边
底角
顶角
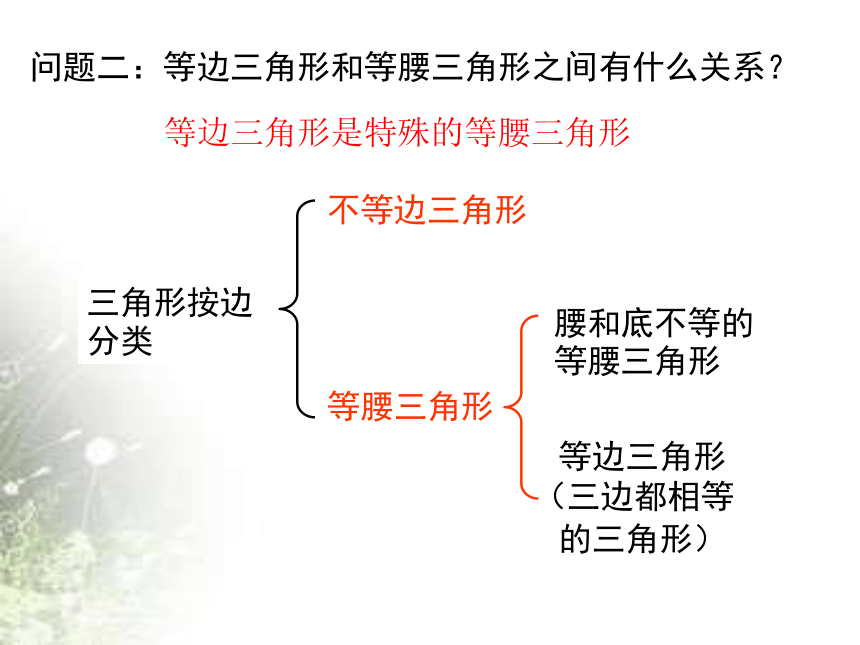
问题二:等边三角形和等腰三角形之间有什么关系?
等边三角形是特殊的等腰三角形
三角形按边分类
不等边三角形
等腰三角形
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
2、等边三角形是特殊的等腰三角形.( )
1、一个钝角三角形一定不是等腰三角形.( )
3、等腰三角形的腰和底一定不相等.( )
判断
√
×
×
4、等边三角形是锐角三角形.( )
√
练习一
二、三角形的三边关系
有人说他一步能走3米,你相信吗?
A
B
C
不可能
小组活动一:
每人都有10根火柴,以1根火柴长为单位长度1,试用1、2、3、4中的任意三个摆出一个三角形,每个只允许用一次,比一比哪组最先摆好,可以摆几个三角形?
是不是有3条线段就能围成三角形呢?
小组活动二:
(1)任意画一个三角形,量出它的三边长度,并填空:
a=______;b=_______;c=______
(2)计算并比较:
a+b____c;b+c____a;c+a____b
a-b____c;b-c____a;c-a____b
(3)通过以上的计算你认为三角形的三边存在怎样的关系?
任意两边之和>第三边
任意两边之差<第三边
两边之差<第三边<两边之和
>
>
>
<
<
<
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形;
取长度为13cm的木棒时,由于5+8=13=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
典例精析
判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
练习二
例2 若三角形的两边长分别为2和7,第三边长为奇数,求第三边的长。
判断三角形边的取值范围:
两边之差<第三边<两边之和.
归纳
解:设第三边的长为x,则7-2<x<7+2,
即5<x<9.
∵x为奇数,
∴x只能是7.
小颖要制作一个三角形木架,现有两根长度8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,∴小颖有5种选法.
所以第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
练习三
当堂练习
1、等腰三角形一边长9cm,另一边长4cm,它的第三边是多少?为什么?
2、为什么经常有些行人斜穿马路而不走人行横道?
人行横道
22cm
理由:
三角形任意两边之和大于第三边。
或者两点之间的所有连线中,线段最短。
4、若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,
得a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
3、如果三角形的两边长分别是2和4,且第三边是奇数,那么第三边长为 。若第三边为偶数,那么三角形的周长 。
3或5
10
分类
解决实际生活问题
解决数学问题
三 角 形
三边关系
性质
课堂小结
4.1 认识三角形
第2课时 三角形的三边关系
在我们的生活中几乎随处可见三角形。它简单,有趣,也十分有用。三角形可以帮助我们更好认识周围世界,解决很多的实际问题。
学习目标
1.掌握三角形按边分类的方法,能够判定三角形
是否为特殊三角形;
2.探索并掌握三角形三边之间的关系,运用三角形
三边关系解决有关问题.(重点、难点)
讲授新课
一、三角形按边分类
问题一:你能找出下列三角形各自的特点吗?
三边均不相等
不等边三角形
有两条边相等
等腰三角形
等边三角形
三条边均相等
腰
底边
底角
顶角
问题二:等边三角形和等腰三角形之间有什么关系?
等边三角形是特殊的等腰三角形
三角形按边分类
不等边三角形
等腰三角形
腰和底不等的等腰三角形
等边三角形(三边都相等
的三角形)
2、等边三角形是特殊的等腰三角形.( )
1、一个钝角三角形一定不是等腰三角形.( )
3、等腰三角形的腰和底一定不相等.( )
判断
√
×
×
4、等边三角形是锐角三角形.( )
√
练习一
二、三角形的三边关系
有人说他一步能走3米,你相信吗?
A
B
C
不可能
小组活动一:
每人都有10根火柴,以1根火柴长为单位长度1,试用1、2、3、4中的任意三个摆出一个三角形,每个只允许用一次,比一比哪组最先摆好,可以摆几个三角形?
是不是有3条线段就能围成三角形呢?
小组活动二:
(1)任意画一个三角形,量出它的三边长度,并填空:
a=______;b=_______;c=______
(2)计算并比较:
a+b____c;b+c____a;c+a____b
a-b____c;b-c____a;c-a____b
(3)通过以上的计算你认为三角形的三边存在怎样的关系?
任意两边之和>第三边
任意两边之差<第三边
两边之差<第三边<两边之和
>
>
>
<
<
<
例1 有两根长度分别为5cm和8cm的木棒,用长度
为2cm的木棒与它们能摆成三角形吗?为什么?长
度为13cm的木棒呢?
判断三条线段是否可以组成三角形,只需
说明两条较短线段之和大于第三条线段即可.
解:取长度为2cm的木棒时,由于2+5=7<8,出现了两边之和小于第三边的情况,所以它们不能摆成三角形;
取长度为13cm的木棒时,由于5+8=13=13,出现了两边之和等于第三边的情况,所以它们也不能摆成三角形.
归纳
典例精析
判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;
(3)5cm、6cm、10cm.
解:(1)不能,因为3cm+4cm<8cm;
(2)不能,因为5cm+6cm=11cm;
(3)能,因为5cm+6cm>10cm.
练习二
例2 若三角形的两边长分别为2和7,第三边长为奇数,求第三边的长。
判断三角形边的取值范围:
两边之差<第三边<两边之和.
归纳
解:设第三边的长为x,则7-2<x<7+2,
即5<x<9.
∵x为奇数,
∴x只能是7.
小颖要制作一个三角形木架,现有两根长度8cm和5cm的木棒,如果要求第三根木棒的长度是偶数,小颖有几种选法?第三根的长度可以是多少?
∵x为偶数,∴小颖有5种选法.
所以第三根木棒的长度可以是4cm,6cm,8cm,10cm,12cm.
解:设第三根木棒长为xcm,有8-5<x<8+5,
即3<x<13.
练习三
当堂练习
1、等腰三角形一边长9cm,另一边长4cm,它的第三边是多少?为什么?
2、为什么经常有些行人斜穿马路而不走人行横道?
人行横道
22cm
理由:
三角形任意两边之和大于第三边。
或者两点之间的所有连线中,线段最短。
4、若a,b,c是△ABC的三边长,化简|a-b-c|+|b-c-a|+|c+a-b|.
解:根据三角形的三边关系,两边之和大于第三边,
得a-b-c<0,b-c-a<0,c+a-b>0.
∴|a-b-c|+|b-c-a|+|c+a-b|
=b+c-a+c+a-b+c+a-b
=3c+a-b.
3、如果三角形的两边长分别是2和4,且第三边是奇数,那么第三边长为 。若第三边为偶数,那么三角形的周长 。
3或5
10
分类
解决实际生活问题
解决数学问题
三 角 形
三边关系
性质
课堂小结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
