人教版七年级下册数学易错题专项训练 5.1相交线(含解析)
文档属性
| 名称 | 人教版七年级下册数学易错题专项训练 5.1相交线(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 17:58:44 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版七年级下册易错题专题
5.1 相交线
一.填空题(共2小题)
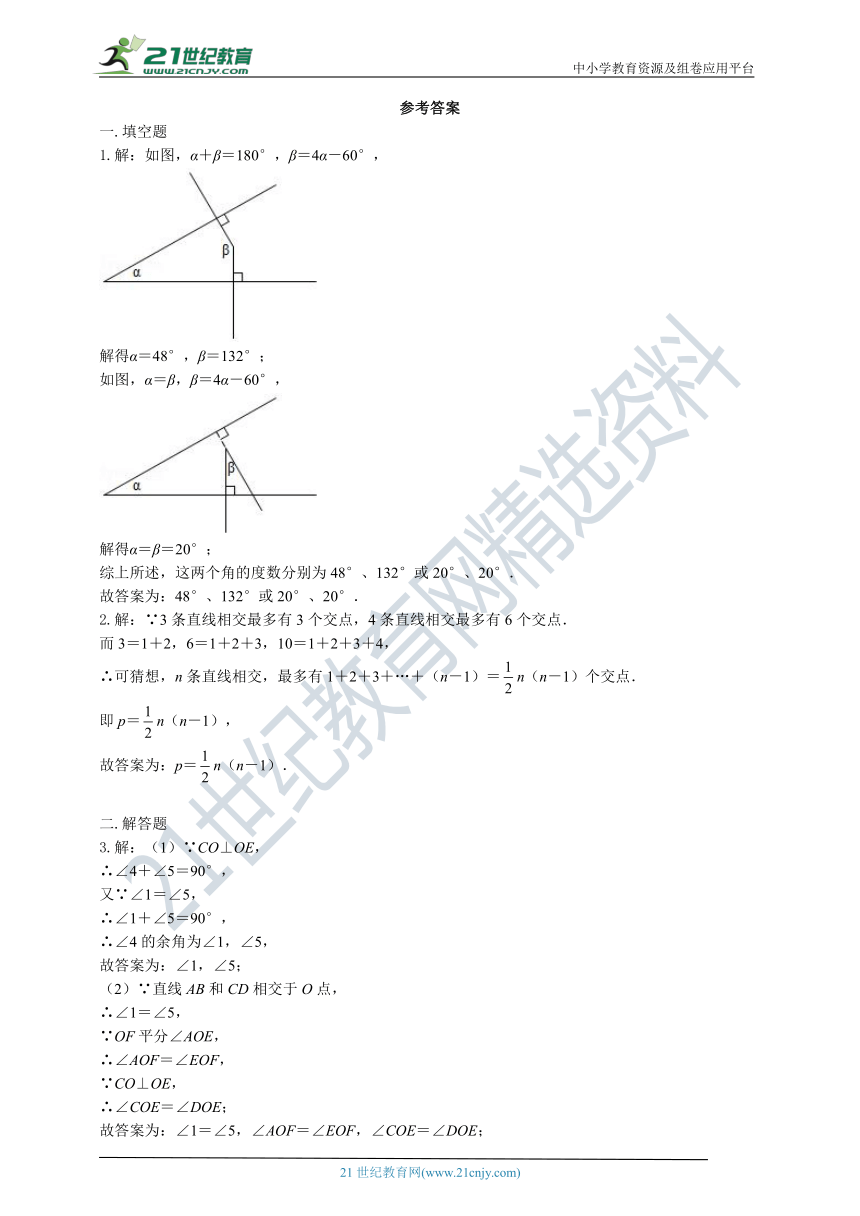
1.如果两个角的两条边分别垂直,而其中一个角比另一个角的4倍少60°,则这两个角的度数分别为 .
2.在一平面中,两条直线相交有一个交点;三条直线两两相交最多有3个交点;四条直线两两相交最多有6个交点……当相交直线的条数从2至n变化时,最多可有的交点数P与直线条数n之间的关系如下表:
直线条数n/条 2 3 4 5 6 7 8 …
最多交点个数p/个 1 3 6 10 … … … …
则n与p的关系式为: .
二.解答题(共8小题)
3.已知直线AB和CD相交于O点,CO⊥OE,OF平分∠AOE,∠2=26°.
(1)写出图中所有∠4的余角 .
(2)写出图中相等的三对角:① ② ③ .
(3)求∠5的度数.
4.如图,直线AB与CD相交于点O,OE是∠AOC的平分线OF⊥CD,OG⊥OE,∠BOD=52°.
(1)求∠AOF的度数;
(2)∠EOF与∠BOG是否相等呢?请说明理由;
(3)直接写出图中∠AOE的所有余角.
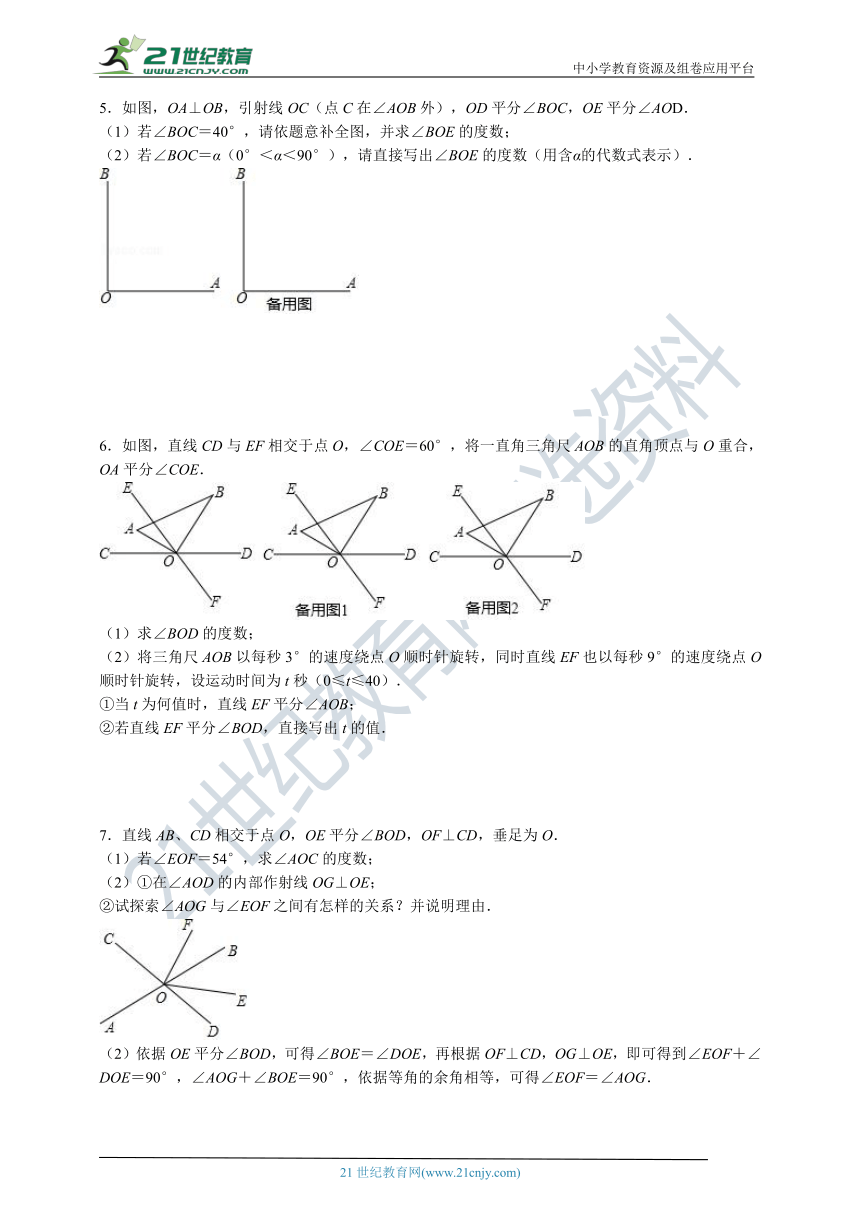
5.如图,OA⊥OB,引射线OC(点C在∠AOB外),OD平分∠BOC,OE平分∠AOD.
(1)若∠BOC=40°,请依题意补全图,并求∠BOE的度数;
(2)若∠BOC=α(0°<α<90°),请直接写出∠BOE的度数(用含α的代数式表示).
6.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
7.直线AB、CD相交于点O,OE平分∠BOD,OF⊥CD,垂足为O.
(1)若∠EOF=54°,求∠AOC的度数;
(2)①在∠AOD的内部作射线OG⊥OE;
②试探索∠AOG与∠EOF之间有怎样的关系?并说明理由.
(2)依据OE平分∠BOD,可得∠BOE=∠DOE,再根据OF⊥CD,OG⊥OE,即可得到∠EOF+∠DOE=90°,∠AOG+∠BOE=90°,依据等角的余角相等,可得∠EOF=∠AOG.
8.如图,直线AB与CD相交于点O,∠BOE=∠DOF=90°.
(1)写出图中与∠COE互补的所有的角(不用说明理由).
(2)问:∠COE与∠AOF相等吗?请说明理由;
(3)如果∠AOC=∠EOF,求∠AOC的度数.
9.如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,∠EOF=90°.若∠BOD=58°,求∠COF的度数.
10.已知直线AB和CD交于点O,∠AOC的度数为x,∠BOE=90°,OF平分∠AOD.
(1)当x=19°48′,求∠EOC与∠FOD的度数.
(2)当x=60°,射线OE、OF分别以10°/s,4°/s的速度同时绕点O顺时针转动,求当射线OE与射线OF重合时至少需要多少时间?
(3)当x=60°,射线OE以10°/s的速度绕点O顺时针转动,同时射线OF也以4°/s的速度绕点O逆时针转动,当射线OE转动一周时射线OF也停止转动.射线OE在转动一周的过程中当∠EOF=90°时,求射线OE转动的时间.
参考答案
一.填空题
1.解:如图,α+β=180°,β=4α-60°,
解得α=48°,β=132°;
如图,α=β,β=4α-60°,
解得α=β=20°;
综上所述,这两个角的度数分别为48°、132°或20°、20°.
故答案为:48°、132°或20°、20°.
2.解:∵3条直线相交最多有3个交点,4条直线相交最多有6个交点.
而3=1+2,6=1+2+3,10=1+2+3+4,
∴可猜想,n条直线相交,最多有1+2+3+…+(n-1)=n(n-1)个交点.
即p=n(n-1),
故答案为:p=n(n-1).
二.解答题
3.解:(1)∵CO⊥OE,
∴∠4+∠5=90°,
又∵∠1=∠5,
∴∠1+∠5=90°,
∴∠4的余角为∠1,∠5,
故答案为:∠1,∠5;
(2)∵直线AB和CD相交于O点,
∴∠1=∠5,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∵CO⊥OE,
∴∠COE=∠DOE;
故答案为:∠1=∠5,∠AOF=∠EOF,∠COE=∠DOE;
(3)∵CO⊥OE,
∴∠COE=90°,
又∵∠COF=26°,
∴∠EOF=90°-26°=64°,
∵OF平分∠AOE,
∴∠AOF=EOF=64°,
∴∠AOC=64°-26°=38°,
∵∠AOC与∠5是对顶角,
∴∠5=38°.
4.解:(1)∵OF⊥CD,
∴∠COF=90°,
又∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=52°,
∴∠AOF=∠COF-∠AOC=90°-52°=38°;
(2)相等,
理由:∵∠AOC与∠BOD是对顶角,
∴∠AOC=∠BOD=52°,
∵OE是∠AOC的平分线,
∴∠AOE=∠AOC=26°,
又∵OG⊥OE,
∴∠EOG=90°,
∴∠BOG=180°-∠AOE-∠EOG=64°,
而∠EOF=∠AOF+∠AOE=38°+26°=64°,
∴∠EOF=∠BOG.
(3)∵OE是∠AOC的平分线,
∴∠AOE=∠COE=26°,
又∵OF⊥CD,
∴∠EOF+∠COE=90°,即∠EOF+∠AOE=90°,
又∵OF⊥CD,OG⊥OE,
∴∠COG=∠EOF,
∴∠COG+∠AOE=90°,
∵∠BOG+∠AOE=90°,∠COG+∠COE=90°,∠AOE=∠COE,
∴∠BOG=∠COG,
∴∠BOG+∠AOE=90°,
∴图中∠AOE的所有余角为∠EOF,∠COG,∠BOG.
5.解:(1)如图,∵OD是∠BOC的平分线,
∴∠COD=∠BOD=20°,
∴∠AOD=∠BOD+∠AOB=20°+90°=110°,
又∵OE是∠AOD的平分线,
∴∠DOE=∠AOD=55°,
∴∠BOE=∠DOE-∠BOD=55°-20°=35°;
(2)同(1)可得∠COD=∠BOD=α,
∠AOD=α+90°,
∠DOE=∠AOD=(α+90°)=α+45°,
则∠BOE=α+45°-α=45°-α.
6.解:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°-30°-90°=60°;
(2)①分两种情况:
当OE平分∠AOB时,∠AOE=45°,
即9t+30°-3t=45°,
解得t=2.5;
当OF平分∠AOB时,AOF=45°,
即9t-150°-3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
当OE平分∠BOD时,∠BOE=∠BOD,
即9t-60°-3t=(60°-3t),
解得t=12;
当OF平分∠BOD时,∠DOF=∠BOD,
即3t-(9t-240°)=(3t-60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
7.解:(1)∵OF⊥CD,∠EOF=54°,
∴∠DOE=90°-54°=36°,
又∵OE平分∠BOD,
∴∠BOD=2∠DOE=72°,
∴∠AOC=72°;
(2)①如图所示:
②∠AOG=∠EOF;
理由:∵OE平分∠BOD,
∴∠BOE=∠DOE,
∵OF⊥CD,OG⊥OE,
∴∠EOF+∠DOE=90°,∠AOG+∠BOE=90°,
∴∠EOF=∠AOG.
8.解:(1)∵直线AB与CD相交于点O,
∴∠COE+∠DOE=180°,
又∵∠BOE=∠DOF=90°,
∴∠DOE=∠BOF,
∴与∠COE互补的所有的角为∠DOE,∠BOF;
(2)∠COE与∠AOF相等,
理由:∵∠BOE=∠DOF=90°,
∴∠AOE=∠COF,
∴∠AOE-∠AOC=∠COF-∠AOC,
∴∠COE=∠AOF;
(3)设∠AOC=x,则∠EOF=5x,
∵∠COE=∠AOF,
∴∠COE=∠AOF=(5x-x)=2x,
∵∠AOE=90°,
∴x+2x=90°,
∴x=30°,
∴∠AOC=30°.
9.解:∵OE是∠BOD的平分线,∠BOD=58°,
∴∠DOE=∠BOD=×58°=29°,
∵∠EOF=90°,
∴∠DOF=∠EOF-∠DOE=90°-29°=61°,
∴∠COF=180°-∠DOF=180°-61°=119°.
10.解:(1)∵∠BOE=90°,
∴∠AOE=90°,
∵∠AOC=x=19°48′,
∴∠EOC=90°-19°48′=89°60°-19°48′=70°12′,
∠AOD=180°-19°48′=160°12′,
∵OF平分∠AOD,
∴∠FOD=∠AOD=×160°12′=80°6′;
(2)当x=60°,∠EOF=90°+60°=150°
设当射线OE与射线OF重合时至少需要t秒,
10t-4t=360-150,
t=35,
答:当射线OE与射线OF重合时至少需要35秒;
(3)设射线OE转动的时间为t秒,
由题意得:10t+90+4t=360-150或10t-(360-150)+4t=90或360-10t=4t-120,
t=或或.
答:射线OE转动的时间为t=秒或秒或秒.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
