北京版七年级下册数学课件:5.1 二元一次方程和它的解 (121张ppt)
文档属性
| 名称 | 北京版七年级下册数学课件:5.1 二元一次方程和它的解 (121张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 00:00:00 | ||
图片预览










文档简介
(共121张PPT)
二元一次方程和它的解
初一年级 数学
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
答对题得的分-答错题扣的分=最后得分
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
答对题数×答对1道题得的分
答错题数×答错1道题扣的分
答对题得的分-答错题扣的分=最后得分
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
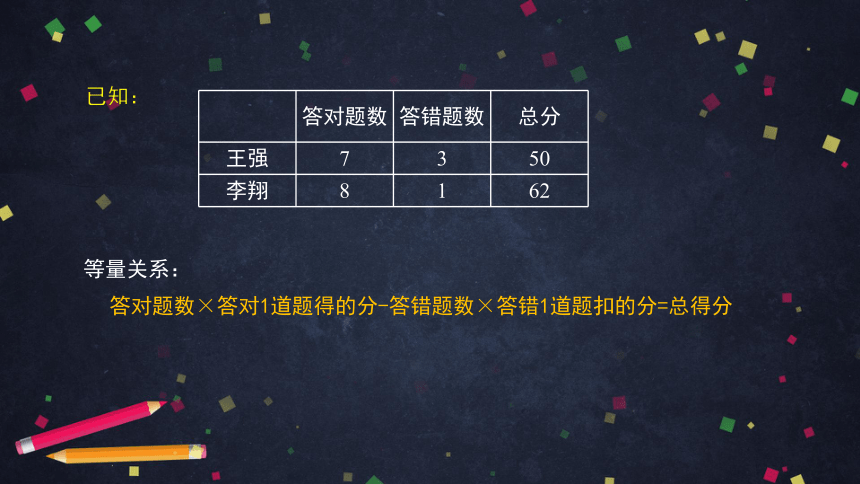
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
等量关系:
答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
等量关系1:
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
等量关系2:
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
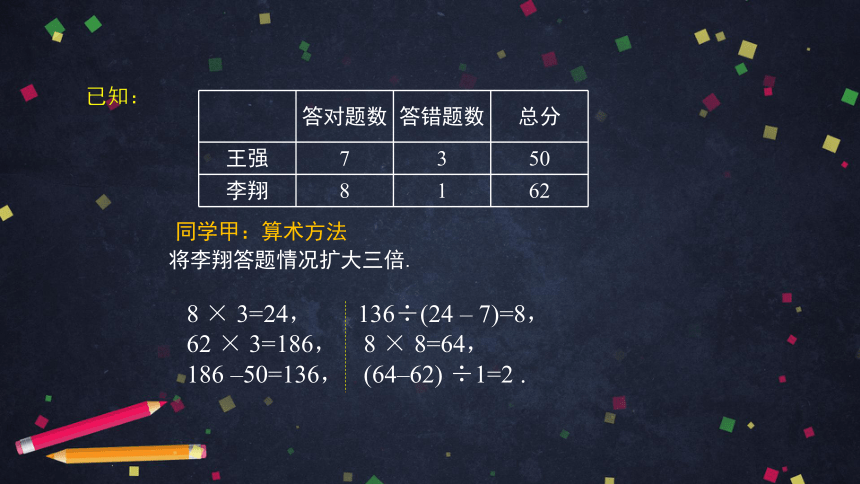
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
同学甲:算术方法
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 24 3 186
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
同学甲:算术方法
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
同学甲:算术方法
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
同学甲:算术方法
答:答对1道题得8分,答错1道题扣2分.
同学乙:列一元一次方程
解:设答对1道题得 分,则答错1道题扣 ? 分 ,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
?
?
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对一题得 分,则答错一题扣 ? 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
?
?
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对一题得 分,则答错一题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对一题得 分,则答错一题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对1道题得 分,则答错1题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
同学乙:列一元一次方程
解:设答对1道题得 分,则答错1道题扣 或 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
或
设两个未知数呢?
设答对1道题得 分,答错1道题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
设两个未知数呢?
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
设答对1道题得 分,答错1道题扣 分,
设两个未知数呢?
注意:设出两个未知数,就要找出两个相等的关系,列出两个方程来表示
问题中的全部含义.
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
设答对1道题得 分,答错1道题扣 分,
问题2:观察上面的两个方程,与一元一次方程有什么相同或不同之处?
类比一元一次方程的概念:
二、类比学习
问题2:观察上面的两个方程,与一元一次方程有什么相同或不同之处?
类比一元一次方程的概念:
二、类比学习
只含有一个未知数,并且未知数的次数是1的整式方程叫做一元一次方程.
例如:
问题2:观察上面的两个方程,与一元一次方程有什么相同或不同之处?
类比一元一次方程的概念:
只含有一个未知数,并且未知数的次数是1的整式方程叫做一元一次方程.
二、类比学习
类比一元一次方程的概念:
二、类比学习
同学观点:
相同:所含未知数的次数都是1;
不同:含有的未知数的个数不同,一元一次方程只含有一个未知数,
而二元一次方程则含有两个未知数.
类比一元一次方程的概念:
二、类比学习
追问1:你能给这两个方程起个名字吗?
类比一元一次方程的概念:
二、类比学习
追问1:你能给这两个方程起个名字吗?
追问2:为什么叫二元一次方程呢?
类比一元一次方程的概念:
二、类比学习
追问1:你能给这两个方程起个名字吗?
追问2:为什么叫二元一次方程呢?
追问3:你能给二元一次方程下定义吗?
类比一元一次方程的概念:
二、类比学习
追问3:你能给二元一次方程下定义吗?
同学观点:含有两个未知数,并且含未知数的次数都是1,就是二元一次方程.
类比一元一次方程的概念:
二、类比学习
追问3:你能给二元一次方程下定义吗?
同学观点:含有两个未知数,并且含未知数的次数都是1,就是二元一次方程.
类比一元一次方程的概念:
二、类比学习
追问3:你能给二元一次方程下定义吗?
同学观点:含有两个未知数,并且含未知数的次数都是1,就是二元一次方程.
反例:
类比一元一次方程的概念:
二、类比学习
二元一次方程定义:含有两个未知数,并且含未知数的项的次数都是1,我们
把这样的方程叫做二元一次方程.
类比一元一次方程的概念:
二、类比学习
二元一次方程定义:含有两个未知数,并且含未知数的项的次数都是1,我们
把这样的方程叫做二元一次方程.
一元一次方程定义:只含有一个未知数,并且未知数的次数是1的整式方程
叫做一元一次方程.
类比一元一次方程的概念:
二、类比学习
二元一次方程特征:
(1)含有两个未知数;
(2)含未知数的项的次数都是1;
(3)整式方程.
类比一元一次方程的概念:
二、类比学习
一元一次方程与二元一次方程的相同点和不同点:
未知数个数 未知数的项的次数
一元一次方程 1个 1次
二元一次方程 2个 1次
类比一元一次方程的概念:
二、类比学习
一元一次方程的一般形式:
( , 是已知数,且 ).
类比一元一次方程的概念:
二、类比学习
一元一次方程的一般形式:
二元一次方程的一般形式:
(其中 是已知数,且 ).
( , 是已知数,且 ).
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
二、类比学习
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
一元二次方程
二、类比学习
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
追问5:你能不能给三元一次方程下定义呢?
一元二次方程
二、类比学习
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
追问5:你能不能给三元一次方程下定义呢?
一元二次方程
含有三个未知数,并且含未知数的项的次数都是1.
二、类比学习
一元一次方程
二元一次方程
三元一次方程
一元二次方程
…
二、类比学习
一元一次方程
二元一次方程
三元一次方程
一元二次方程
一元三次方程
…
…
二、类比学习
例:判断下列方程中哪些是二元一次方程?
经典例题:
例:判断下列方程中哪些是二元一次方程?
不是
经典例题:
例:判断下列方程中哪些是二元一次方程?
是
不是
经典例题:
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
经典例题:
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
经典例题:
不是
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
不是
经典例题:
不是
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
经典例题:
不是
注意:(1)含有两个未知数;
(2)含未知数的项的次数都是1.
不是
例: 方程 是关于 的二元一次方程, 求 的值.
关于
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
是未知数,
未知数的项的系数不能为0,
含未知数的项的次数都为1.
解析:
关于
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
又
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
又
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
又
二元一次方程的解?
二、类比学习
类比方程解的概念:
一般地,能够使方程左、右两边的值相等的未知数的值叫做方程的解.
二、类比学习
类比方程解的概念:
一般地,能够使方程左、右两边的值相等的未知数的值叫做方程的解.
例如:当 时,方程 左右两边的值相等,
二、类比学习
记作
我们就把 叫做方程 的一个解,
注意:
(1)用大括号联立;
(2)二元一次方程有两个未知数,所以二元一次方程的解是一对未知数的值;
(3)两个数之间是“且”的关系,要同时成立.
二、类比学习
二、类比学习
二元一次方程的一个解:
使二元一次方程左右两边的值相等的一对未知数的值,叫做这个二元
一次方程的一个解.
记作
类比方程解的概念:
一般地,能够使方程左、右两边的值相等的未知数的值叫做方程的解.
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
∵方程左边 右边
二、类比学习
∴左边=右边
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
∵方程左边 右边
二、类比学习
∴ 是方程 的一个解.
∴左边=右边.
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
∵方程左边 右边
二、类比学习
∴ 是方程 的一个解.
∴左边=右边.
判断 是不是方程 的一个解?
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 ...
... 5 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 ...
... 5 4 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 ...
... 5 4 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 ...
... 5 4 3 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 6 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 6 ...
... 5 4 3 0 ...
解:
(1)当 时,得到方程 ,
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 6 ...
... 5 4 3 0 ...
解:
(1)当 时,得到方程 ,解这个方程得到 ;
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 5 6 ...
... 5 4 3 0 ...
2
(2)当 时,得到方程 ,解这个方程得到 ;
解:
(1)当 时,得到方程 ,解这个方程得到 ;
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 4 5 6 ...
... 5 4 3 1 0 ...
2
(2)当 时,得到方程 ,解这个方程得到 ;
解:
(1)当 时,得到方程 ,解这个方程得到 ;
(3)当 时,得到方程 ,解这个方程得到 ;
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 4 5 6 ...
... 5 4 3 1 0 ...
2
7
(2)当 时,得到方程 ,解这个方程得到 ;
解:
(1)当 时,得到方程 ,解这个方程得到 ;
(3)当 时,得到方程 ,解这个方程得到 ;
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 4 5 6 ...
... 5 4 3 1 0 ...
2
7
解:
(4)当 时,得到方程 ,解这个方程得到 .
.
思考如何求方程 的解.
方法小结:
只要我们给出 (或 )的一个值,把它代入方程中,就可以将方程转化
为含有另一个未知数 (或 )的一元一次方程,从而求出相应的 (或 )
的一个值,这一对 , 的值就是这个二元一次方程的一个解.
方法小结:
只要我们给出 (或 )的一个值,把它代入方程中,就可以将方程转化
为含有另一个未知数 (或 )的一元一次方程,从而求出相应的 (或 )
的一个值,这一对 , 的值就是这个二元一次方程的一个解.
二元一次方程
代入x(或y)
一个确定的值
消元转化
关于y (或x)的
一元一次方程
等式基本性质
变形转化
求出y(或x)
方法小结:
只要我们给出 (或 )的一个值,把它代入方程中,就可以将方程转化
为含有另一个未知数 (或 )的一元一次方程,从而求出相应的 (或 )
的一个值,这一对 , 的值就是这个二元一次方程的一个解.
二元一次方程
代入x(或y)
一个确定的值
消元转化
关于y (或x)的
一元一次方程
等式基本性质
变形转化
求出y(或x)
未知
已知
简单
复杂
知识小结:
一般地,一个二元一次方程有无数多个解,即二元一次方程的解具
有不确定性. 二元一次方程中的未知数是互相联系、相互制约的关系.
追问2:请你判断 是不是方程 的一个解.
解:∵方程左边 ,右边 ,
追问2:请你判断 是不是方程 的一个解.
解:∵方程左边 ,右边 ,
∴ 不是方程 的一个解.
∴左边 右边.
∴
追问2:请你判断 是不是方程 的一个解.
注意:不是任何一个数对都是二元一次方程的一个解.
解:∵方程左边 ,右边 ,
∴ 不是方程 的一个解.
∴左边 右边.
∴
追问2:请你判断 是不是方程 的一个解.
注意:不是任何一个数对都是二元一次方程的一个解.
解:∵方程左边 ,右边 ,
∴ 不是方程 的一个解.
∴左边 右边.
∴
数
等量代换
代入
式
运算
求值
方程
追问2:请你判断 是不是方程 的一个解.
追问3:写出方程 所有的正整数解.
解: ∵ 均为正整数,
∴
∴ 为小于5的正整数,
是方程所有的正整数解.
追问3:写出方程 所有的正整数解.
解: ∵ 均为正整数,
注意:在 的值的选取上,不是随意代入一个正整数,应按从小到大或从大到小的顺序选取,以免重漏.
∴
∴ 为小于5的正整数,
是方程所有的正整数解.
追问3:写出方程 所有的正整数解.
小结:
一元一次方程与二元一次方程解的相同点和不同点:
类比一元一次方程的解
未知数个数 未知数的项的次数 方程解的个数
一元一次方程 1个 1次 唯一1个
二元一次方程 2个 1次 无数个
例
已知: ,用含 y的代数式表示 x .
经典例题:
例
解:由
已知: ,用含 的代数式表示 .
移项,得
(等式基本性质1)
经典例题:
得
例
解:由
已知: ,用含 的代数式表示 .
移项,得
系数化为1 ,得
(等式基本性质1)
(等式基本性质2)
经典例题:
得
例
解:方法二:由
已知: ,用含 的代数式表示 .
两边同时除以2,得
(等式基本性质2)
经典例题:
得
例
解:方法二:由
已知: ,用含 的代数式表示 .
两边同时除以2,得
移项,得
(等式基本性质2)
(等式基本性质1)
经典例题:
得
例
解:由
已知: ,用含 的代数式表示 .
移项,得
系数化为1 ,得
(等式基本性质1)
(等式基本性质2)
经典例题:
得
当 时,代入得
方法小结:
“用含有一个未知数的代数式表示另一个未知数,再赋值”的方法.
利用求代数式的值的方法解决.
二元一次方程
等式基本性质
变形转化
赋值代入
消元转化
解
一元一次方程
方法小结:
方法一:“先给出的一个值,转化为一元一次方程,从而求出相应的的值;
方法二:“用含有一个未知数的代数式表示另一个未知数,再赋值”的方法.利用求代数式的值的方法解决.
二元一次方程
一元一次方程
赋值代入
消元转化
解
变形转化
等式基本性质
二元一次方程
等式基本性质
变形转化
一元一次方程
赋值代入
消元转化
解
方法一:先赋值,后变形,再求解;
方法二:先变形,后赋值,再求解.
两种方法的区别与联系:
方法小结:
方法一:先赋值,后变形,再求解;
方法二:先变形,后赋值,再求解.
二元一次方程
代入消元
转化
一元一次方程
两种方法的区别与联系:
方法小结:
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
引导:把其中一个未知数当作已知数
解: 或
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
引导:把其中一个未知数当作已知数
解: 或
或
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
从具体到抽象,从特殊到一般.
引导:把其中一个未知数当作已知数
解: 或
或
三、课堂小结:
(1)二元一次方程
含有两个未知数,并且含未知数的项的次数都是1,我们把这样的方程
叫做二元一次方程.
(2)二元一次方程的解
使二元一次方程左右两边的值相等的一对未知数的值叫做这个二元
一次方程的一个解,二元一次方程的解具有不确定性.
1.知识梳理
(3)一元一次方程和二元一次方程及其解的区别与联系:
未知数个数 未知数的项的次数 方程解的个数
一元一次方程 1个 1次 唯一1个
二元一次方程 2个 1次 无数个
三、课堂小结:
1.知识梳理
二元一次方程
一元一次方程
赋值代入
消元转化
解
等式基本性质
变形转化
二元一次方程
等式基本性质
变形转化
一元一次方程
赋值代入
消元转化
解
二元一次方程
代入消元
转化
一元一次方程
三、课堂小结:
2.解题方法
运用了方程思想、建模思想、转化、化归思想、函数思想.
类比方法,从具体到抽象,从特殊到一般.
三、课堂小结:
3.数学思想方法
4.研究方法
1.把下列二元一次方程改写成用含有一个未知数的代数式表示另一个
未知数的形式:
(1)
(2)
(3)
四、课后作业:
2. 填写下表,使表中的每一对 , 的值都是方程 的一个解:
四、课后作业:
3. 是不是方程 和 的公共解?
是不是方程 和 的公共解?请你检验一下.
4.求满足方程 的非负整数解.
四、课后作业:
一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程.因此,一旦解决了方程问题,一切问题将迎刃而解.
——笛卡尔
?
二元一次方程和它的解
初一年级 数学
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
答对题得的分-答错题扣的分=最后得分
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
答对题数×答对1道题得的分
答错题数×答错1道题扣的分
答对题得的分-答错题扣的分=最后得分
一、引入新知:
问题1:在新年联欢会上同学们组织了猜谜活动,并采取积分方法记分,每
答对1题要得分,每答错1题要扣分.在猜谜活动中,王强答对了7道题,答错
了3道题,共获得50分;李翔答对了8道题,答错了1道题,共获得62分.
问答对1道题得多少分,答错1道题扣多少分.
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
等量关系:
答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
等量关系1:
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
等量关系2:
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
同学甲:算术方法
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 24 3 186
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
同学甲:算术方法
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
同学甲:算术方法
将李翔答题情况扩大三倍.
8 × 3=24, 136÷(24 ? 7)=8,
62 × 3=186, 8 × 8=64,
186 ?50=136, (64?62) ÷1=2 .
已知:
答对题数 答错题数 总分
王强 7 3 50
李翔 8 1 62
同学甲:算术方法
答:答对1道题得8分,答错1道题扣2分.
同学乙:列一元一次方程
解:设答对1道题得 分,则答错1道题扣 ? 分 ,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
?
?
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对一题得 分,则答错一题扣 ? 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
?
?
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对一题得 分,则答错一题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对一题得 分,则答错一题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
同学乙:列一元一次方程
解:设答对1道题得 分,则答错1题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
同学乙:列一元一次方程
解:设答对1道题得 分,则答错1道题扣 或 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
或
设两个未知数呢?
设答对1道题得 分,答错1道题扣 分,
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
设两个未知数呢?
王强:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
李翔:答对题数×答对1道题得的分-答错题数×答错1道题扣的分=总得分
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
设答对1道题得 分,答错1道题扣 分,
设两个未知数呢?
注意:设出两个未知数,就要找出两个相等的关系,列出两个方程来表示
问题中的全部含义.
答对题数
对1题得分数
答错题数
总分
错1题扣分数
王强
李翔
7
3
50
8
1
62
设答对1道题得 分,答错1道题扣 分,
问题2:观察上面的两个方程,与一元一次方程有什么相同或不同之处?
类比一元一次方程的概念:
二、类比学习
问题2:观察上面的两个方程,与一元一次方程有什么相同或不同之处?
类比一元一次方程的概念:
二、类比学习
只含有一个未知数,并且未知数的次数是1的整式方程叫做一元一次方程.
例如:
问题2:观察上面的两个方程,与一元一次方程有什么相同或不同之处?
类比一元一次方程的概念:
只含有一个未知数,并且未知数的次数是1的整式方程叫做一元一次方程.
二、类比学习
类比一元一次方程的概念:
二、类比学习
同学观点:
相同:所含未知数的次数都是1;
不同:含有的未知数的个数不同,一元一次方程只含有一个未知数,
而二元一次方程则含有两个未知数.
类比一元一次方程的概念:
二、类比学习
追问1:你能给这两个方程起个名字吗?
类比一元一次方程的概念:
二、类比学习
追问1:你能给这两个方程起个名字吗?
追问2:为什么叫二元一次方程呢?
类比一元一次方程的概念:
二、类比学习
追问1:你能给这两个方程起个名字吗?
追问2:为什么叫二元一次方程呢?
追问3:你能给二元一次方程下定义吗?
类比一元一次方程的概念:
二、类比学习
追问3:你能给二元一次方程下定义吗?
同学观点:含有两个未知数,并且含未知数的次数都是1,就是二元一次方程.
类比一元一次方程的概念:
二、类比学习
追问3:你能给二元一次方程下定义吗?
同学观点:含有两个未知数,并且含未知数的次数都是1,就是二元一次方程.
类比一元一次方程的概念:
二、类比学习
追问3:你能给二元一次方程下定义吗?
同学观点:含有两个未知数,并且含未知数的次数都是1,就是二元一次方程.
反例:
类比一元一次方程的概念:
二、类比学习
二元一次方程定义:含有两个未知数,并且含未知数的项的次数都是1,我们
把这样的方程叫做二元一次方程.
类比一元一次方程的概念:
二、类比学习
二元一次方程定义:含有两个未知数,并且含未知数的项的次数都是1,我们
把这样的方程叫做二元一次方程.
一元一次方程定义:只含有一个未知数,并且未知数的次数是1的整式方程
叫做一元一次方程.
类比一元一次方程的概念:
二、类比学习
二元一次方程特征:
(1)含有两个未知数;
(2)含未知数的项的次数都是1;
(3)整式方程.
类比一元一次方程的概念:
二、类比学习
一元一次方程与二元一次方程的相同点和不同点:
未知数个数 未知数的项的次数
一元一次方程 1个 1次
二元一次方程 2个 1次
类比一元一次方程的概念:
二、类比学习
一元一次方程的一般形式:
( , 是已知数,且 ).
类比一元一次方程的概念:
二、类比学习
一元一次方程的一般形式:
二元一次方程的一般形式:
(其中 是已知数,且 ).
( , 是已知数,且 ).
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
二、类比学习
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
一元二次方程
二、类比学习
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
追问5:你能不能给三元一次方程下定义呢?
一元二次方程
二、类比学习
追问4:如果含有一个未知数,并且含未知数的项的最高次数是2,
那么它叫什么方程呢?
追问5:你能不能给三元一次方程下定义呢?
一元二次方程
含有三个未知数,并且含未知数的项的次数都是1.
二、类比学习
一元一次方程
二元一次方程
三元一次方程
一元二次方程
…
二、类比学习
一元一次方程
二元一次方程
三元一次方程
一元二次方程
一元三次方程
…
…
二、类比学习
例:判断下列方程中哪些是二元一次方程?
经典例题:
例:判断下列方程中哪些是二元一次方程?
不是
经典例题:
例:判断下列方程中哪些是二元一次方程?
是
不是
经典例题:
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
经典例题:
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
经典例题:
不是
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
不是
经典例题:
不是
例:判断下列方程中哪些是二元一次方程?
是
不是
不是
经典例题:
不是
注意:(1)含有两个未知数;
(2)含未知数的项的次数都是1.
不是
例: 方程 是关于 的二元一次方程, 求 的值.
关于
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
是未知数,
未知数的项的系数不能为0,
含未知数的项的次数都为1.
解析:
关于
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
又
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
又
例: 方程 是关于 的二元一次方程, 求 的值.
∵ 方程 是关于 的二元一次方程.
解:
经典例题:
又
二元一次方程的解?
二、类比学习
类比方程解的概念:
一般地,能够使方程左、右两边的值相等的未知数的值叫做方程的解.
二、类比学习
类比方程解的概念:
一般地,能够使方程左、右两边的值相等的未知数的值叫做方程的解.
例如:当 时,方程 左右两边的值相等,
二、类比学习
记作
我们就把 叫做方程 的一个解,
注意:
(1)用大括号联立;
(2)二元一次方程有两个未知数,所以二元一次方程的解是一对未知数的值;
(3)两个数之间是“且”的关系,要同时成立.
二、类比学习
二、类比学习
二元一次方程的一个解:
使二元一次方程左右两边的值相等的一对未知数的值,叫做这个二元
一次方程的一个解.
记作
类比方程解的概念:
一般地,能够使方程左、右两边的值相等的未知数的值叫做方程的解.
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
∵方程左边 右边
二、类比学习
∴左边=右边
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
∵方程左边 右边
二、类比学习
∴ 是方程 的一个解.
∴左边=右边.
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
判断 是不是方程 的一个解?
二、类比学习
类比一元一次方程的解:
问题3: 请你写出方程 的一个解.
∵方程左边 右边
二、类比学习
∴ 是方程 的一个解.
∴左边=右边.
判断 是不是方程 的一个解?
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 ...
... 5 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 ...
... 5 4 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 ...
... 5 4 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 ...
... 5 4 3 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 6 ...
... 5 4 3 0 ...
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 6 ...
... 5 4 3 0 ...
解:
(1)当 时,得到方程 ,
追问1:二元一次方程有多少个解呢?
思考如何求方程 的解.
... 0 1 2 5 6 ...
... 5 4 3 0 ...
解:
(1)当 时,得到方程 ,解这个方程得到 ;
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 5 6 ...
... 5 4 3 0 ...
2
(2)当 时,得到方程 ,解这个方程得到 ;
解:
(1)当 时,得到方程 ,解这个方程得到 ;
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 4 5 6 ...
... 5 4 3 1 0 ...
2
(2)当 时,得到方程 ,解这个方程得到 ;
解:
(1)当 时,得到方程 ,解这个方程得到 ;
(3)当 时,得到方程 ,解这个方程得到 ;
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 4 5 6 ...
... 5 4 3 1 0 ...
2
7
(2)当 时,得到方程 ,解这个方程得到 ;
解:
(1)当 时,得到方程 ,解这个方程得到 ;
(3)当 时,得到方程 ,解这个方程得到 ;
思考如何求方程 的解.
追问1:二元一次方程有多少个解呢?
... 0 1 2 3 4 5 6 ...
... 5 4 3 1 0 ...
2
7
解:
(4)当 时,得到方程 ,解这个方程得到 .
.
思考如何求方程 的解.
方法小结:
只要我们给出 (或 )的一个值,把它代入方程中,就可以将方程转化
为含有另一个未知数 (或 )的一元一次方程,从而求出相应的 (或 )
的一个值,这一对 , 的值就是这个二元一次方程的一个解.
方法小结:
只要我们给出 (或 )的一个值,把它代入方程中,就可以将方程转化
为含有另一个未知数 (或 )的一元一次方程,从而求出相应的 (或 )
的一个值,这一对 , 的值就是这个二元一次方程的一个解.
二元一次方程
代入x(或y)
一个确定的值
消元转化
关于y (或x)的
一元一次方程
等式基本性质
变形转化
求出y(或x)
方法小结:
只要我们给出 (或 )的一个值,把它代入方程中,就可以将方程转化
为含有另一个未知数 (或 )的一元一次方程,从而求出相应的 (或 )
的一个值,这一对 , 的值就是这个二元一次方程的一个解.
二元一次方程
代入x(或y)
一个确定的值
消元转化
关于y (或x)的
一元一次方程
等式基本性质
变形转化
求出y(或x)
未知
已知
简单
复杂
知识小结:
一般地,一个二元一次方程有无数多个解,即二元一次方程的解具
有不确定性. 二元一次方程中的未知数是互相联系、相互制约的关系.
追问2:请你判断 是不是方程 的一个解.
解:∵方程左边 ,右边 ,
追问2:请你判断 是不是方程 的一个解.
解:∵方程左边 ,右边 ,
∴ 不是方程 的一个解.
∴左边 右边.
∴
追问2:请你判断 是不是方程 的一个解.
注意:不是任何一个数对都是二元一次方程的一个解.
解:∵方程左边 ,右边 ,
∴ 不是方程 的一个解.
∴左边 右边.
∴
追问2:请你判断 是不是方程 的一个解.
注意:不是任何一个数对都是二元一次方程的一个解.
解:∵方程左边 ,右边 ,
∴ 不是方程 的一个解.
∴左边 右边.
∴
数
等量代换
代入
式
运算
求值
方程
追问2:请你判断 是不是方程 的一个解.
追问3:写出方程 所有的正整数解.
解: ∵ 均为正整数,
∴
∴ 为小于5的正整数,
是方程所有的正整数解.
追问3:写出方程 所有的正整数解.
解: ∵ 均为正整数,
注意:在 的值的选取上,不是随意代入一个正整数,应按从小到大或从大到小的顺序选取,以免重漏.
∴
∴ 为小于5的正整数,
是方程所有的正整数解.
追问3:写出方程 所有的正整数解.
小结:
一元一次方程与二元一次方程解的相同点和不同点:
类比一元一次方程的解
未知数个数 未知数的项的次数 方程解的个数
一元一次方程 1个 1次 唯一1个
二元一次方程 2个 1次 无数个
例
已知: ,用含 y的代数式表示 x .
经典例题:
例
解:由
已知: ,用含 的代数式表示 .
移项,得
(等式基本性质1)
经典例题:
得
例
解:由
已知: ,用含 的代数式表示 .
移项,得
系数化为1 ,得
(等式基本性质1)
(等式基本性质2)
经典例题:
得
例
解:方法二:由
已知: ,用含 的代数式表示 .
两边同时除以2,得
(等式基本性质2)
经典例题:
得
例
解:方法二:由
已知: ,用含 的代数式表示 .
两边同时除以2,得
移项,得
(等式基本性质2)
(等式基本性质1)
经典例题:
得
例
解:由
已知: ,用含 的代数式表示 .
移项,得
系数化为1 ,得
(等式基本性质1)
(等式基本性质2)
经典例题:
得
当 时,代入得
方法小结:
“用含有一个未知数的代数式表示另一个未知数,再赋值”的方法.
利用求代数式的值的方法解决.
二元一次方程
等式基本性质
变形转化
赋值代入
消元转化
解
一元一次方程
方法小结:
方法一:“先给出的一个值,转化为一元一次方程,从而求出相应的的值;
方法二:“用含有一个未知数的代数式表示另一个未知数,再赋值”的方法.利用求代数式的值的方法解决.
二元一次方程
一元一次方程
赋值代入
消元转化
解
变形转化
等式基本性质
二元一次方程
等式基本性质
变形转化
一元一次方程
赋值代入
消元转化
解
方法一:先赋值,后变形,再求解;
方法二:先变形,后赋值,再求解.
两种方法的区别与联系:
方法小结:
方法一:先赋值,后变形,再求解;
方法二:先变形,后赋值,再求解.
二元一次方程
代入消元
转化
一元一次方程
两种方法的区别与联系:
方法小结:
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
引导:把其中一个未知数当作已知数
解: 或
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
引导:把其中一个未知数当作已知数
解: 或
或
思考:
怎样确定二元一次方程 (其中 , , 是已知数,且
, )的一个解.
从具体到抽象,从特殊到一般.
引导:把其中一个未知数当作已知数
解: 或
或
三、课堂小结:
(1)二元一次方程
含有两个未知数,并且含未知数的项的次数都是1,我们把这样的方程
叫做二元一次方程.
(2)二元一次方程的解
使二元一次方程左右两边的值相等的一对未知数的值叫做这个二元
一次方程的一个解,二元一次方程的解具有不确定性.
1.知识梳理
(3)一元一次方程和二元一次方程及其解的区别与联系:
未知数个数 未知数的项的次数 方程解的个数
一元一次方程 1个 1次 唯一1个
二元一次方程 2个 1次 无数个
三、课堂小结:
1.知识梳理
二元一次方程
一元一次方程
赋值代入
消元转化
解
等式基本性质
变形转化
二元一次方程
等式基本性质
变形转化
一元一次方程
赋值代入
消元转化
解
二元一次方程
代入消元
转化
一元一次方程
三、课堂小结:
2.解题方法
运用了方程思想、建模思想、转化、化归思想、函数思想.
类比方法,从具体到抽象,从特殊到一般.
三、课堂小结:
3.数学思想方法
4.研究方法
1.把下列二元一次方程改写成用含有一个未知数的代数式表示另一个
未知数的形式:
(1)
(2)
(3)
四、课后作业:
2. 填写下表,使表中的每一对 , 的值都是方程 的一个解:
四、课后作业:
3. 是不是方程 和 的公共解?
是不是方程 和 的公共解?请你检验一下.
4.求满足方程 的非负整数解.
四、课后作业:
一切问题都可以转化为数学问题,一切数学问题都可以转化为代数问题,而一切代数问题又都可以转化为方程.因此,一旦解决了方程问题,一切问题将迎刃而解.
——笛卡尔
?
同课章节目录
- 第四章 一元一次不等式和一元一次不等式组
- 4.1 不等式
- 4.2 不等式的基本性质
- 4.3 不等式的解集
- 4.4 一元一次不等式及其解法
- 4.5 一元一次不等式组及其解法
- 第五章 二元一次方程组
- 5.1 二元一次方程和它的解
- 5.2 二元一次方程组和它的解
- 5.3 用代入消元法解二元一次方程组
- 5.4 用加减消元法解二元一次方程组
- *5.5 三元一次方程组
- 5.6 二元一次方程组的应用
- 第六章 整式的运算
- 6.1 整式的加减法
- 6.2 幂的运算
- 6.3 整式的乘法
- 6.4 乘法公式
- 6.5 整式的除法
- 第七章 观察、猜想与证明
- 7.1 观察
- 7.2 实验
- 7.3 归纳
- 7.4 类比
- 7.5 猜想
- 7.6 证明
- 7.7 几种简单几何图形及其推理
- 第八章 因式分解
- 8.1 因式分解
- 8.2 提公因式法
- 8.3 公式法
- 第九章 数据的收集与表示
- 9.1 总体与样本
- 9.2 数据的收集与整理
- 9.3 数据的表示——扇形统计图
- 9.4 用计算机绘制统计图
- 9.5 平均数
- 9.6 众数和中位数
