六年级下册数学课件 正比例、反比例整理和复习 苏教版 (共15张PPT)
文档属性
| 名称 | 六年级下册数学课件 正比例、反比例整理和复习 苏教版 (共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 264.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 14:41:30 | ||
图片预览






文档简介
(共15张PPT)
正比例、反比例整理和复习
正比例、反比例
1、什么叫做正比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的商一定,那么这两种量成正比例关系。
=
y
x
_
K(一定)
2、什么叫做反比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,那么这两种量成反比例关系。
Xy=k(一定)
3、正比例和反比例的区别
比例 相同点 不同点
正比例
反比例
两种相关联的量,一种量变化,另一种量也随着变化。
两种量的变化,同时扩大或同时缩小
一种量扩大,另一种量反而缩小。
商一定
积一定
4、如何判断是否成正比例、反比例关系。
方法:“一找、二想、三判断”
一找:哪两种量;
二想:两种相关联量的变化情况,写出关系式。
三判断:联系关系式,看商一定还是积一定,判断成什么比例。
5、举例
(1)被除数÷除数=商(一定)
(2)除数×商=被除数(一定)
(3)因数×因数=积(一定)
(4)积÷因数=因数(一定)
(正比例关系)
(反比例关系)
(反比例关系)
(正比例关系)
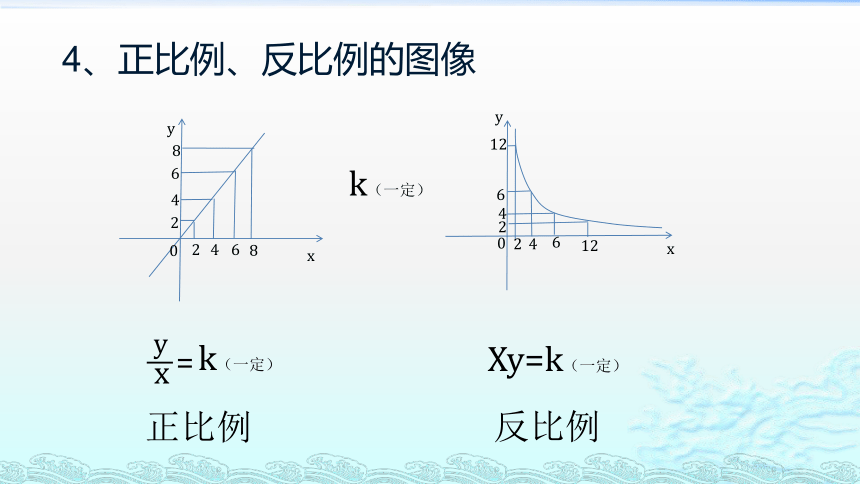
4、正比例、反比例的图像
正比例
反比例
0
2
4
6
8
2
4
6
8
y
x
0
2
4
2
4
6
12
12
6
y
x
k(一定)
y
x
—
=
k(一定)
Xy=k(一定)
试一试:
火眼金睛(判断下面各题的两个量是否成比例?如果成比例,成什么比例关系?)
(1)做一个零件的时间一定,做的零件总个数和总时间。( )
(2)减数一定,被减数与差。( )
不成比例关系
正比例关系
做的零件总个数
总时间
=
做一个零件的时间(一定)
被减数—差=减数(一定)
(3)小明拿一些钱购买铅笔,单价和购买的数量。( )
(4)圆的周长与直径。( )
单价×购买数量=总价(一定)
反比例关系
C
d
—
=
∏(一定)
正比例关系
练习与实践第7题
比的前项 0.3 2 5
比的后项 6 40 100
小麦的质量∕kg 5 10 15
磨面粉的质量∕kg 3.5 7 10.5
2
40
—
=
0.05
5
100
—
=
0.05
0.3
6
—
=
0.05
3.5
5
—
=
0.7
10.5
15
—
=
0.7
比的前项
比的后项
=
比值(一定)
磨面粉的质量
小麦的质量
=
出粉率(一定)
比的前项和比的后项成正比例
小麦的质量和磨面粉的质量成正比例
三角形的底∕cm 8 12 16
三角形的高∕cm 6 4 3
圆的半径∕cm 1 2 3
圆的面积∕kg 3.14 12.56 28.26
8 ×6=48 12 ×4=48 16 ×3=48
三角形的底×三角形的高=
三角形的底和三角形的高成反比例
圆的半径和圆的面积不成比例
积(一定)
8.判断各题的两种量是否成比例,成比例的是成正比例还是反
比例?
(1)步测一段距离,每步的平均长度和走的步数。
答:每步的平均长度和走的步数成反比例。
(2)一台压路机滚筒滚动的转数和压路的面积。
答:一台压路机滚筒滚动的转数和压路的面积成正比例。
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间。
答:麦地面积和收割时间成正比例。
每步的平均长度×走的步数=总米数(一定)
压路的总面积
滚动的转数
滚筒滚动一圈压路的面积(一定)
=
麦地总面积
收割时间
每小时收割麦子的面积(一定)
=
(4)图书室的藏书数量一定,每天借出和还回的书的本数。
答:每天借出和还回的书的本数不成比例。
(5)已知 x y = 10, x 和 y。
答: x和y成反比例。
x× y = 10(一定)
答:这辆汽车在高速公路上行驶的路程和耗油量成正比例,
因为每升油行驶的路程是一定的。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
拓展练习
答:行驶75千米耗油6升。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(2)根据图像判断?行驶75
千米耗油多少升?
75
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(3)汽车在市区行驶,每行50千米耗油 6升, 照这样的耗油
量,在上图中描出行驶50千米、100 千米… …路程和耗
油量对应的点,再按顺序连接起来。
(2)根据图像判断?行驶75
千米耗油多少升?
谢谢!
正比例、反比例整理和复习
正比例、反比例
1、什么叫做正比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的商一定,那么这两种量成正比例关系。
=
y
x
_
K(一定)
2、什么叫做反比例?
两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的积一定,那么这两种量成反比例关系。
Xy=k(一定)
3、正比例和反比例的区别
比例 相同点 不同点
正比例
反比例
两种相关联的量,一种量变化,另一种量也随着变化。
两种量的变化,同时扩大或同时缩小
一种量扩大,另一种量反而缩小。
商一定
积一定
4、如何判断是否成正比例、反比例关系。
方法:“一找、二想、三判断”
一找:哪两种量;
二想:两种相关联量的变化情况,写出关系式。
三判断:联系关系式,看商一定还是积一定,判断成什么比例。
5、举例
(1)被除数÷除数=商(一定)
(2)除数×商=被除数(一定)
(3)因数×因数=积(一定)
(4)积÷因数=因数(一定)
(正比例关系)
(反比例关系)
(反比例关系)
(正比例关系)
4、正比例、反比例的图像
正比例
反比例
0
2
4
6
8
2
4
6
8
y
x
0
2
4
2
4
6
12
12
6
y
x
k(一定)
y
x
—
=
k(一定)
Xy=k(一定)
试一试:
火眼金睛(判断下面各题的两个量是否成比例?如果成比例,成什么比例关系?)
(1)做一个零件的时间一定,做的零件总个数和总时间。( )
(2)减数一定,被减数与差。( )
不成比例关系
正比例关系
做的零件总个数
总时间
=
做一个零件的时间(一定)
被减数—差=减数(一定)
(3)小明拿一些钱购买铅笔,单价和购买的数量。( )
(4)圆的周长与直径。( )
单价×购买数量=总价(一定)
反比例关系
C
d
—
=
∏(一定)
正比例关系
练习与实践第7题
比的前项 0.3 2 5
比的后项 6 40 100
小麦的质量∕kg 5 10 15
磨面粉的质量∕kg 3.5 7 10.5
2
40
—
=
0.05
5
100
—
=
0.05
0.3
6
—
=
0.05
3.5
5
—
=
0.7
10.5
15
—
=
0.7
比的前项
比的后项
=
比值(一定)
磨面粉的质量
小麦的质量
=
出粉率(一定)
比的前项和比的后项成正比例
小麦的质量和磨面粉的质量成正比例
三角形的底∕cm 8 12 16
三角形的高∕cm 6 4 3
圆的半径∕cm 1 2 3
圆的面积∕kg 3.14 12.56 28.26
8 ×6=48 12 ×4=48 16 ×3=48
三角形的底×三角形的高=
三角形的底和三角形的高成反比例
圆的半径和圆的面积不成比例
积(一定)
8.判断各题的两种量是否成比例,成比例的是成正比例还是反
比例?
(1)步测一段距离,每步的平均长度和走的步数。
答:每步的平均长度和走的步数成反比例。
(2)一台压路机滚筒滚动的转数和压路的面积。
答:一台压路机滚筒滚动的转数和压路的面积成正比例。
(3)一台收割机每小时收割麦子的面积一定,麦地面积和收割时间。
答:麦地面积和收割时间成正比例。
每步的平均长度×走的步数=总米数(一定)
压路的总面积
滚动的转数
滚筒滚动一圈压路的面积(一定)
=
麦地总面积
收割时间
每小时收割麦子的面积(一定)
=
(4)图书室的藏书数量一定,每天借出和还回的书的本数。
答:每天借出和还回的书的本数不成比例。
(5)已知 x y = 10, x 和 y。
答: x和y成反比例。
x× y = 10(一定)
答:这辆汽车在高速公路上行驶的路程和耗油量成正比例,
因为每升油行驶的路程是一定的。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
拓展练习
答:行驶75千米耗油6升。
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(2)根据图像判断?行驶75
千米耗油多少升?
75
9. 右图表示一辆汽车在高速
公路上行驶的路程和耗油
量的关系。
(1)这辆汽车在高速公路上
行驶的路程和耗油量成
正比例吗?为什么?
(3)汽车在市区行驶,每行50千米耗油 6升, 照这样的耗油
量,在上图中描出行驶50千米、100 千米… …路程和耗
油量对应的点,再按顺序连接起来。
(2)根据图像判断?行驶75
千米耗油多少升?
谢谢!
