人教版数学七年级下册5.1.1对顶角与邻补角学案(含解析)
文档属性
| 名称 | 人教版数学七年级下册5.1.1对顶角与邻补角学案(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 158.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 15:14:48 | ||
图片预览

文档简介
5.1.1对顶角与邻补角
知识精讲
一.对顶角
概念 如果两个角有公共顶点,并且它们的两边互为反向延长线,则这两个角叫做对顶角. 两条直线相交成四个角,其中不相邻的两个角叫对顶角.
特征 两个角有公共顶点,其两边互为反向延长线.
性质 对顶角相等.
?
二.邻补角
概念 两个角有一条公共边,它们的另一条边互为反向延长线,则这两个角互为邻补角.
特征 1.具有一个公共的顶点; 2.有一条公共边; 3.两个角的另一边互为反向延长线; 4.邻补角是成对出现的,而且是互为邻补角.
性质 互为邻补角的两角之和为.
?题型精讲
例:和、和是对顶角,和、和、和、和是邻补角.
?
三.易错点
1.若两个角互为对顶角,则他们一定相等;反之,若两个角相等,则他们不一定互为对顶角;
2.补角与邻补角的区别和联系:邻补角一定是互补的,但互补的两个角不一定是邻补角;一个角的补角可以有很多个,但邻补角最多有两个.
3.只有两条直线相交时才能产生对顶角,对顶角是成对出现的.
例题精讲
题型一:对顶角
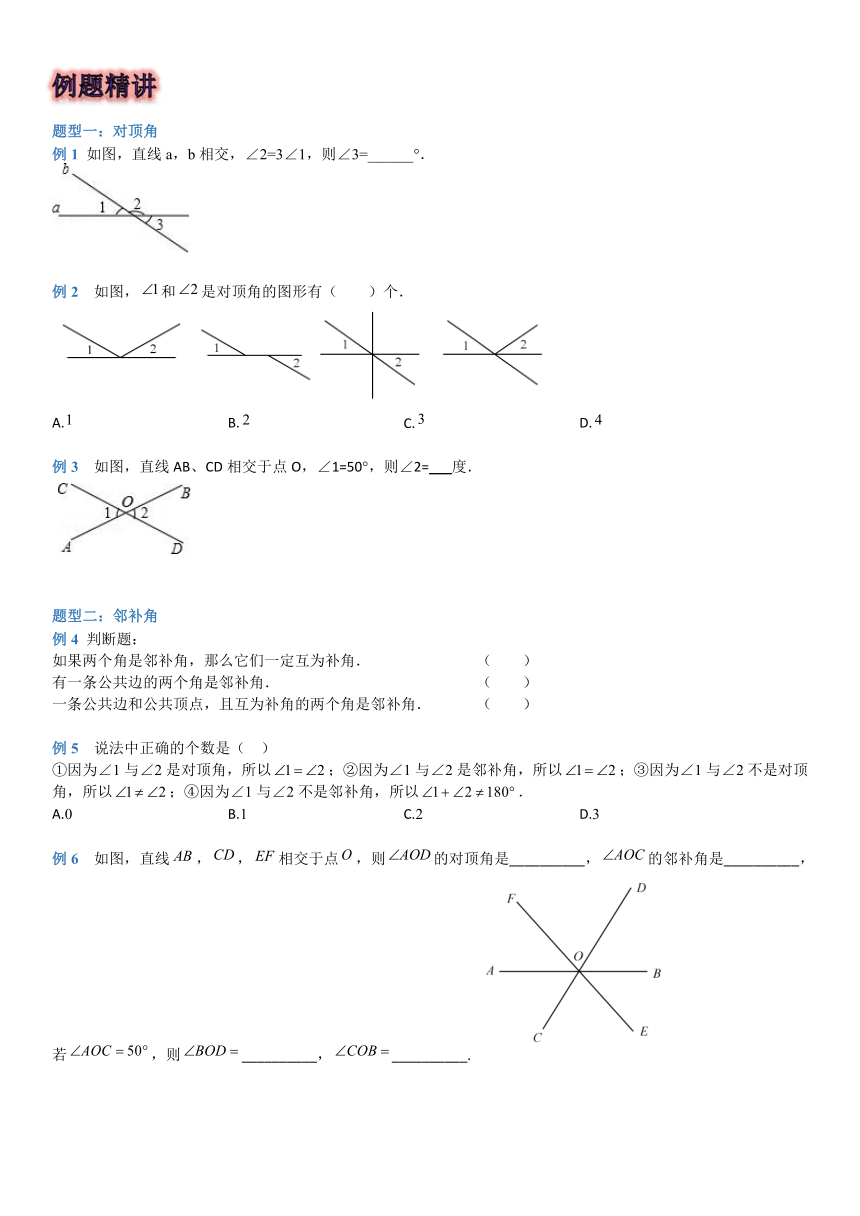
例1 如图,直线a,b相交,∠2=3∠1,则∠3=______°.
例2 如图,和是对顶角的图形有( )个.
A. B. C. D.
例3 如图,直线AB、CD相交于点O,∠1=50°,则∠2=___度.
题型二:邻补角
例4 判断题:
如果两个角是邻补角,那么它们一定互为补角. ( )
有一条公共边的两个角是邻补角. ( )
一条公共边和公共顶点,且互为补角的两个角是邻补角. ( )
例5 说法中正确的个数是( )
①因为∠1与∠2是对顶角,所以;②因为∠1与∠2是邻补角,所以;③因为∠1与∠2不是对顶角,所以;④因为∠1与∠2不是邻补角,所以.
A.0 B.1 C.2 D.3
例6 如图,直线,,相交于点,则的对顶角是__________,的邻补角是__________,若,则__________,__________.
课堂练习
随练1 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
A.100° B.120° C.140° D.160°
随练2 如图,∠1和∠2是对顶角的是( )
A. B.
C. D.
随练3 如图所示,直线AB,CD相交于O,若∠1=∠2,则∠2=____度.
随练4 如图,直线AB、CD相交于点O,对顶角有__________对,它们分别是__________,∠AOD的邻补角是__________.
答案解析
例1
【答案】45
【解析】由图示得,∠1与∠2互为邻补角,即∠1+∠2=180°,
又∵∠2=3∠1,
∴∠1+3∠1=180°,
∴∠1=45°,
∴∠3=∠1=45°.
例2
【答案】A
【解析】如果两个角有公共顶点,并且它们的两边互为反向延长线,则这两个角叫做对顶角,只有第三个图符合,所以答案为A选项.
例3
【答案】50°
【解析】∠2=∠1=50°
例4
【答案】对,错,对
【解析】邻补角一定互为补角,互为补角不一定是邻补角,所以①对;两个角有一条公共边,它们的另一条边互为反向延长线,则这两个角互为邻补角,所以②错,③对.
例5
【答案】B
【解析】①正确;②中(邻补角性质);③中当∠1与∠2是邻补角且时;④在“∠1与∠2在同一个图形”的前提下成立.
例6
【答案】,或,50°,130°.
【解析】根据对顶角和邻补角的定义即可.
随练1
【答案】C
【解析】由对顶角相等,得
∠1=∠2,又∠1+∠2=80°,
得∠1=40°.
由邻补角的定义,得
∠3=180°﹣∠1=180°﹣40°=140°,
故选:C.
随练2
【答案】B
【解析】A、不是对顶角,故本选项错误;
B、是对顶角,故本选项正确;
C、不是对顶角,故本选项错误;
D、不是对顶角,故本选项错误.
随练3
【答案】140°
【解析】∵∠1+∠2=180°,
∵∠1=∠2,
∴∠2+∠2=180°,
解得:∠2=140°,
随练4
【答案】2;∠AOC与∠BOD、∠AOD与∠BOC;∠AOC与∠BOD
【解析】由图可知对顶角有两对分别为∠AOC与∠BOD,∠AOD与∠BOC;
由图可知,,所以∠AOD的邻补角为∠AOC和∠BOD.
知识精讲
一.对顶角
概念 如果两个角有公共顶点,并且它们的两边互为反向延长线,则这两个角叫做对顶角. 两条直线相交成四个角,其中不相邻的两个角叫对顶角.
特征 两个角有公共顶点,其两边互为反向延长线.
性质 对顶角相等.
?
二.邻补角
概念 两个角有一条公共边,它们的另一条边互为反向延长线,则这两个角互为邻补角.
特征 1.具有一个公共的顶点; 2.有一条公共边; 3.两个角的另一边互为反向延长线; 4.邻补角是成对出现的,而且是互为邻补角.
性质 互为邻补角的两角之和为.
?题型精讲
例:和、和是对顶角,和、和、和、和是邻补角.
?
三.易错点
1.若两个角互为对顶角,则他们一定相等;反之,若两个角相等,则他们不一定互为对顶角;
2.补角与邻补角的区别和联系:邻补角一定是互补的,但互补的两个角不一定是邻补角;一个角的补角可以有很多个,但邻补角最多有两个.
3.只有两条直线相交时才能产生对顶角,对顶角是成对出现的.
例题精讲
题型一:对顶角
例1 如图,直线a,b相交,∠2=3∠1,则∠3=______°.
例2 如图,和是对顶角的图形有( )个.
A. B. C. D.
例3 如图,直线AB、CD相交于点O,∠1=50°,则∠2=___度.
题型二:邻补角
例4 判断题:
如果两个角是邻补角,那么它们一定互为补角. ( )
有一条公共边的两个角是邻补角. ( )
一条公共边和公共顶点,且互为补角的两个角是邻补角. ( )
例5 说法中正确的个数是( )
①因为∠1与∠2是对顶角,所以;②因为∠1与∠2是邻补角,所以;③因为∠1与∠2不是对顶角,所以;④因为∠1与∠2不是邻补角,所以.
A.0 B.1 C.2 D.3
例6 如图,直线,,相交于点,则的对顶角是__________,的邻补角是__________,若,则__________,__________.
课堂练习
随练1 如图,直线AB与CD相交于点O,若∠1+∠2=80°,则∠3等于( )
A.100° B.120° C.140° D.160°
随练2 如图,∠1和∠2是对顶角的是( )
A. B.
C. D.
随练3 如图所示,直线AB,CD相交于O,若∠1=∠2,则∠2=____度.
随练4 如图,直线AB、CD相交于点O,对顶角有__________对,它们分别是__________,∠AOD的邻补角是__________.
答案解析
例1
【答案】45
【解析】由图示得,∠1与∠2互为邻补角,即∠1+∠2=180°,
又∵∠2=3∠1,
∴∠1+3∠1=180°,
∴∠1=45°,
∴∠3=∠1=45°.
例2
【答案】A
【解析】如果两个角有公共顶点,并且它们的两边互为反向延长线,则这两个角叫做对顶角,只有第三个图符合,所以答案为A选项.
例3
【答案】50°
【解析】∠2=∠1=50°
例4
【答案】对,错,对
【解析】邻补角一定互为补角,互为补角不一定是邻补角,所以①对;两个角有一条公共边,它们的另一条边互为反向延长线,则这两个角互为邻补角,所以②错,③对.
例5
【答案】B
【解析】①正确;②中(邻补角性质);③中当∠1与∠2是邻补角且时;④在“∠1与∠2在同一个图形”的前提下成立.
例6
【答案】,或,50°,130°.
【解析】根据对顶角和邻补角的定义即可.
随练1
【答案】C
【解析】由对顶角相等,得
∠1=∠2,又∠1+∠2=80°,
得∠1=40°.
由邻补角的定义,得
∠3=180°﹣∠1=180°﹣40°=140°,
故选:C.
随练2
【答案】B
【解析】A、不是对顶角,故本选项错误;
B、是对顶角,故本选项正确;
C、不是对顶角,故本选项错误;
D、不是对顶角,故本选项错误.
随练3
【答案】140°
【解析】∵∠1+∠2=180°,
∵∠1=∠2,
∴∠2+∠2=180°,
解得:∠2=140°,
随练4
【答案】2;∠AOC与∠BOD、∠AOD与∠BOC;∠AOC与∠BOD
【解析】由图可知对顶角有两对分别为∠AOC与∠BOD,∠AOD与∠BOC;
由图可知,,所以∠AOD的邻补角为∠AOC和∠BOD.
