人教版八年级下册数学课件:17.2 勾股定理的逆定理 (46张ppt)
文档属性
| 名称 | 人教版八年级下册数学课件:17.2 勾股定理的逆定理 (46张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 18:47:02 | ||
图片预览






文档简介
(共46张PPT)
初二年级 数学
勾股定理的逆定理
复习旧知
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么 .
勾股定理
∵在Rt 中,∠C=90°,(已知)
∴ .(勾股定理)
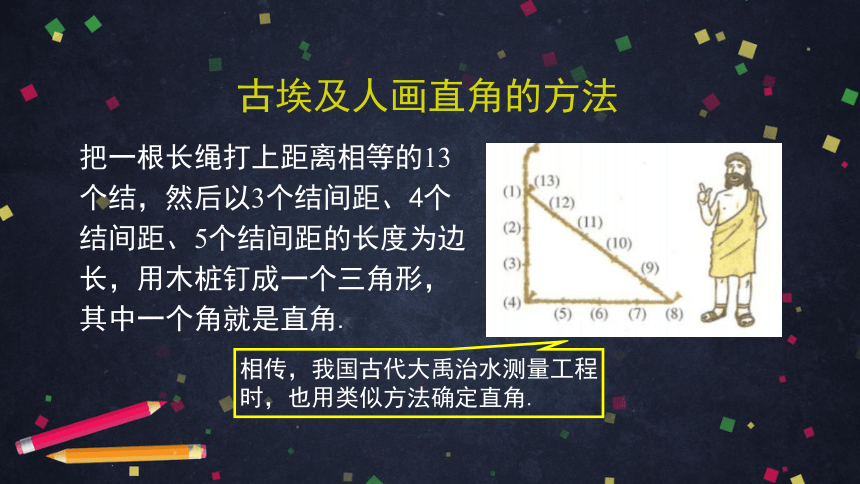
把一根长绳打上距离相等的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角就是直角.
古埃及人画直角的方法
相传,我国古代大禹治水测量工程时,也用类似方法确定直角.
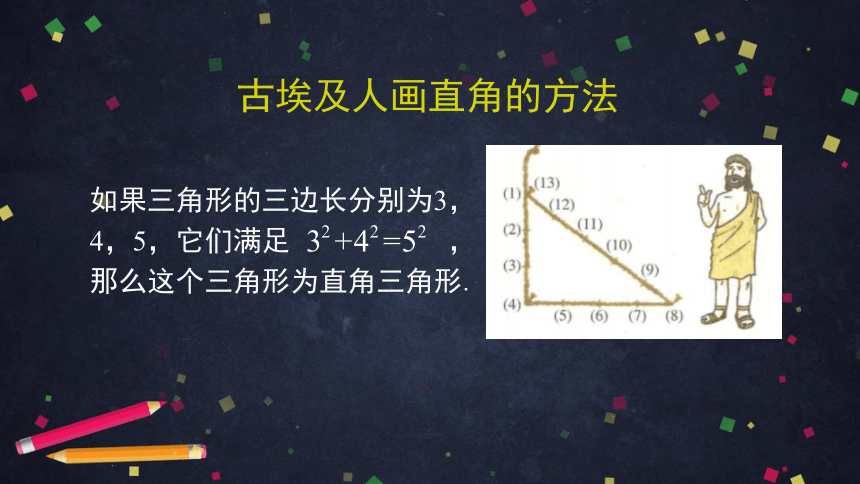
如果三角形的三边长分别为3,4,5,它们满足 , 那么这个三角形为直角三角形.
古埃及人画直角的方法
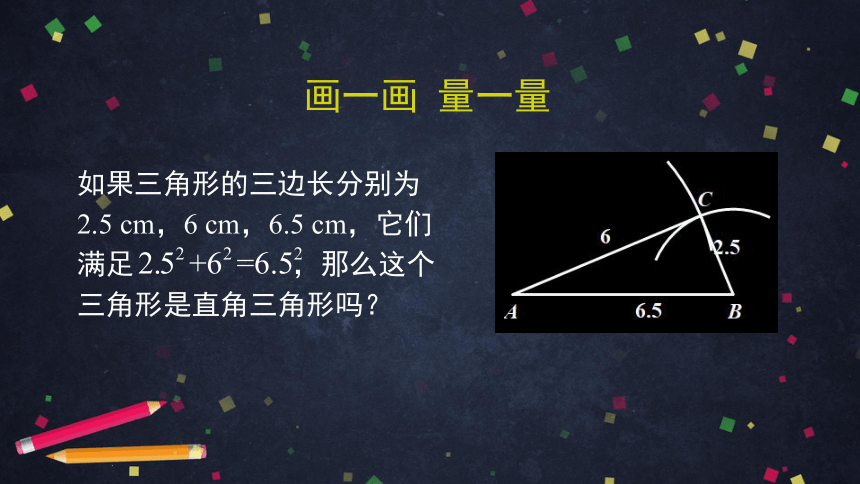
如果三角形的三边长分别为2.5 cm,6 cm,6.5 cm,它们满足 ,那么这个三角形是直角三角形吗?
画一画 量一量
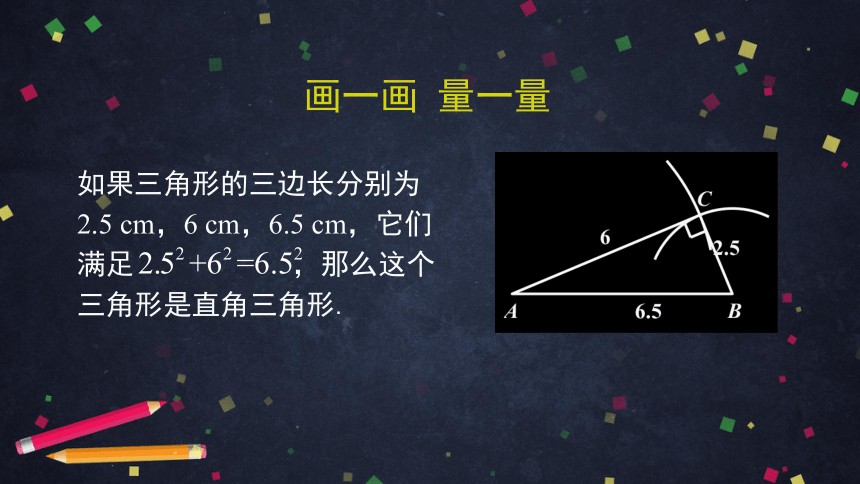
画一画 量一量
如果三角形的三边长分别为2.5 cm,6 cm,6.5 cm,它们满足 ,那么这个三角形是直角三角形.
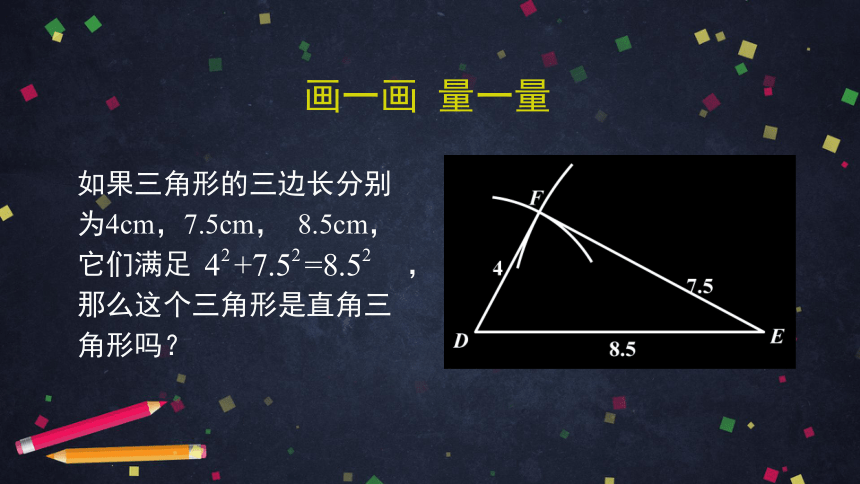
如果三角形的三边长分别为4cm,7.5cm, 8.5cm,它们满足 , 那么这个三角形是直角三角形吗?
画一画 量一量
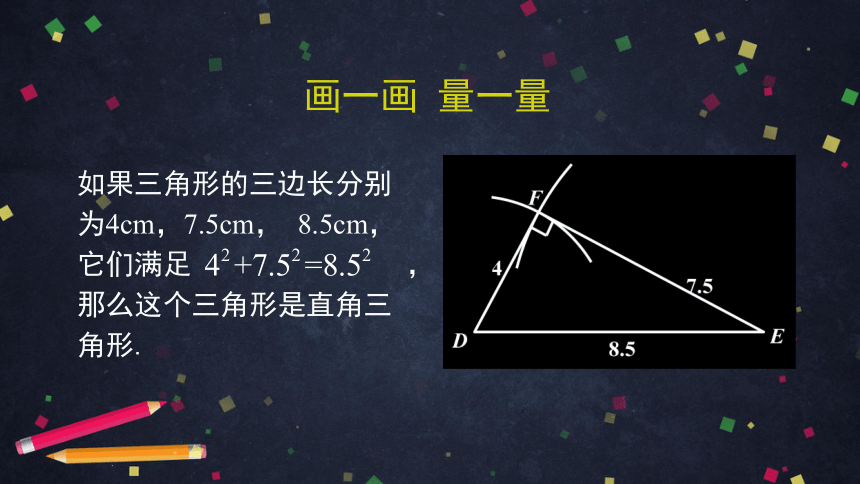
画一画 量一量
如果三角形的三边长分别为4cm,7.5cm, 8.5cm,它们满足 , 那么这个三角形是直角三角形.
看一看 想一想
如果三角形的三边长分别为
3, 4, 5 ,它们满足 ,
那么这个三角形为直角三角形.
看一看 想一想
如果三角形的三边长分别为
2.5,6,6.5 ,它们满足 ,
那么这个三角形为直角三角形.
看一看 想一想
如果三角形的三边长分别为
4,7.5,8.5 ,它们满足 ,
那么这个三角形为直角三角形.
如果三角形的三边长分别为a,b,c,它们满足 , 那么这个三角形是直角三角形.
猜 想
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
证明:画Rt ,使 ,
, , .
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
证明:在Rt 中, ,
, .
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
证明:在 和 中, ,
是直角三角形.
,
.
.
如果三角形的三边长分别为a,b,c,满足 , 那么这个三角形是直角三角形.
勾股定理的逆定理
逆命题
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么 .
勾股定理
原命题
判定直角三角形的一个依据
互 逆 命 题
归 纳
∵在 中, ,(已知)
∴ 是直角三角形.(勾股定理的逆定理)
勾股定理的逆定理
如果三角形的三边长分别为a,b,c,满足 , 那么这个三角形是直角三角形.
应 用
分析:首先找出原命题的题设和结论,将它们互换得到逆命题,然后再判断逆命题是否成立.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
对顶角相等.
(2)
应 用
分析:原命题的题设:内错角相等,
原命题的结论:两直线平行.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
应 用
解:逆命题:两直线平行,内错角相等,这是平行线的性
质定理,显然成立.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
应 用
原命题的题设:两个角是对顶角,结论:这两个角相等.
例1 写出下列命题的逆命题,这些逆命题成立吗?
对顶角相等.
(2)
分析:为了便于寻找原命题题设和结论,我们把原命题改写成“如果… ,那么….”的形式.
原命题:如果两个角是对顶角,那么这两个角相等.
应 用
这个命题显然不成立,因为两个角相等是数量关系,
而对顶角则是有特殊位置关系的角,它们不存在因
果关系.
例1 写出下列命题的逆命题,这些逆命题成立吗?
对顶角相等.
(2)
解:逆命题:如果两个角相等,那么这两个角是对顶角.
应 用
归纳:原命题与逆命题的题设和结论正好相反.有些命题在找题设和结论时要恰当的组织语言。原命题成立,它的逆命题不一定成立.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
对顶角相等.
(2)
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
分析:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
(1) , , ;
(2) , , .
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
解: ,
,
是直角三角形.
(1) , , ;
.
.
解: , .
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
是最大边的长.
(2) , , .
, .
,
,
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
解:
(2) , , .
,
,
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
是直角三角形.
解:
(2) , , .
应 用
例2 判断由下面三条线段组成的三角形是否是直角三角形?
归纳:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
(1) , , ;
(2) , , .
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
分析:正方形ABCD,提供直角三角形:
.
E、F的位置,使直角三角形的直角边边长间具备特殊的数量关系.
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
分析:要证 ,需根据勾股
定理的逆定理判断 .
所以需要在直角三角形:
中应用勾股定理分别计算线段
的长度.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:∵四边形ABCD是正方形,
.
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:设
.
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:∵E是BC的中点,
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:在Rt 中,
(勾股定理)
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:在Rt 中,
(勾股定理)
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:在Rt 中,
(勾股定理)
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:
(勾股定理的逆定理)
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
归纳:首先从已知分析图形的结构,然后从求证寻找解题的方向,最后综合运用勾股定理和勾股定理的逆定理解决问题.
小 结
1. 勾股定理的逆定理;
2. 原命题与逆命题.
题设和结论恰好相反
判定直角三角形的一个依据
知
识
小 结
3. 如何得到勾股定理的逆定理的?
4. 如何证明勾股定理的逆定理?
构造直角三角形
方
法
特殊 一般
猜想 证明
作 业
1.写出下列命题的逆命题,这些命题的逆命题成立吗?
(1) 同旁内角互补,两条直线平行;
(2) 如果两个实数相等,那么它们的平方相等.
2.判断由下面线段组成的三角形是不是直角三角形:(1) , , ;
(2) , , .
作 业
3. 在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,
求四边形ABCD的面积.
祝同学们每天都有新收获!
初二年级 数学
勾股定理的逆定理
复习旧知
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么 .
勾股定理
∵在Rt 中,∠C=90°,(已知)
∴ .(勾股定理)
把一根长绳打上距离相等的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角就是直角.
古埃及人画直角的方法
相传,我国古代大禹治水测量工程时,也用类似方法确定直角.
如果三角形的三边长分别为3,4,5,它们满足 , 那么这个三角形为直角三角形.
古埃及人画直角的方法
如果三角形的三边长分别为2.5 cm,6 cm,6.5 cm,它们满足 ,那么这个三角形是直角三角形吗?
画一画 量一量
画一画 量一量
如果三角形的三边长分别为2.5 cm,6 cm,6.5 cm,它们满足 ,那么这个三角形是直角三角形.
如果三角形的三边长分别为4cm,7.5cm, 8.5cm,它们满足 , 那么这个三角形是直角三角形吗?
画一画 量一量
画一画 量一量
如果三角形的三边长分别为4cm,7.5cm, 8.5cm,它们满足 , 那么这个三角形是直角三角形.
看一看 想一想
如果三角形的三边长分别为
3, 4, 5 ,它们满足 ,
那么这个三角形为直角三角形.
看一看 想一想
如果三角形的三边长分别为
2.5,6,6.5 ,它们满足 ,
那么这个三角形为直角三角形.
看一看 想一想
如果三角形的三边长分别为
4,7.5,8.5 ,它们满足 ,
那么这个三角形为直角三角形.
如果三角形的三边长分别为a,b,c,它们满足 , 那么这个三角形是直角三角形.
猜 想
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
证明:画Rt ,使 ,
, , .
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
证明:在Rt 中, ,
, .
已知: 的三边长分别为a,b,c,它们满足 , 求证: 是直角三角形.
证 明
证明:在 和 中, ,
是直角三角形.
,
.
.
如果三角形的三边长分别为a,b,c,满足 , 那么这个三角形是直角三角形.
勾股定理的逆定理
逆命题
如果直角三角形的两直角边长分别为a,b,斜边长为c,
那么 .
勾股定理
原命题
判定直角三角形的一个依据
互 逆 命 题
归 纳
∵在 中, ,(已知)
∴ 是直角三角形.(勾股定理的逆定理)
勾股定理的逆定理
如果三角形的三边长分别为a,b,c,满足 , 那么这个三角形是直角三角形.
应 用
分析:首先找出原命题的题设和结论,将它们互换得到逆命题,然后再判断逆命题是否成立.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
对顶角相等.
(2)
应 用
分析:原命题的题设:内错角相等,
原命题的结论:两直线平行.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
应 用
解:逆命题:两直线平行,内错角相等,这是平行线的性
质定理,显然成立.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
应 用
原命题的题设:两个角是对顶角,结论:这两个角相等.
例1 写出下列命题的逆命题,这些逆命题成立吗?
对顶角相等.
(2)
分析:为了便于寻找原命题题设和结论,我们把原命题改写成“如果… ,那么….”的形式.
原命题:如果两个角是对顶角,那么这两个角相等.
应 用
这个命题显然不成立,因为两个角相等是数量关系,
而对顶角则是有特殊位置关系的角,它们不存在因
果关系.
例1 写出下列命题的逆命题,这些逆命题成立吗?
对顶角相等.
(2)
解:逆命题:如果两个角相等,那么这两个角是对顶角.
应 用
归纳:原命题与逆命题的题设和结论正好相反.有些命题在找题设和结论时要恰当的组织语言。原命题成立,它的逆命题不一定成立.
例1 写出下列命题的逆命题,这些逆命题成立吗?
内错角相等,两条直线平行;
(1)
对顶角相等.
(2)
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
分析:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
(1) , , ;
(2) , , .
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
解: ,
,
是直角三角形.
(1) , , ;
.
.
解: , .
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
是最大边的长.
(2) , , .
, .
,
,
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
解:
(2) , , .
,
,
应 用
例2 判断由下面三条线段组成的三角形是不是直角三角形?
是直角三角形.
解:
(2) , , .
应 用
例2 判断由下面三条线段组成的三角形是否是直角三角形?
归纳:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
(1) , , ;
(2) , , .
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
分析:正方形ABCD,提供直角三角形:
.
E、F的位置,使直角三角形的直角边边长间具备特殊的数量关系.
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
分析:要证 ,需根据勾股
定理的逆定理判断 .
所以需要在直角三角形:
中应用勾股定理分别计算线段
的长度.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:∵四边形ABCD是正方形,
.
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:设
.
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:∵E是BC的中点,
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:在Rt 中,
(勾股定理)
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:在Rt 中,
(勾股定理)
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:在Rt 中,
(勾股定理)
.
.
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
证明:
(勾股定理的逆定理)
应 用
例3 在正方形ABCD中,E是BC的中点,F是CD上一点,
且 ,求证:
归纳:首先从已知分析图形的结构,然后从求证寻找解题的方向,最后综合运用勾股定理和勾股定理的逆定理解决问题.
小 结
1. 勾股定理的逆定理;
2. 原命题与逆命题.
题设和结论恰好相反
判定直角三角形的一个依据
知
识
小 结
3. 如何得到勾股定理的逆定理的?
4. 如何证明勾股定理的逆定理?
构造直角三角形
方
法
特殊 一般
猜想 证明
作 业
1.写出下列命题的逆命题,这些命题的逆命题成立吗?
(1) 同旁内角互补,两条直线平行;
(2) 如果两个实数相等,那么它们的平方相等.
2.判断由下面线段组成的三角形是不是直角三角形:(1) , , ;
(2) , , .
作 业
3. 在四边形ABCD中,AB=3,BC=4,CD=12,AD=13,
求四边形ABCD的面积.
祝同学们每天都有新收获!
