北京版八年级下册数学课件:14.6 一次函数的性质(第二课时) (40张ppt)
文档属性
| 名称 | 北京版八年级下册数学课件:14.6 一次函数的性质(第二课时) (40张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 00:00:00 | ||
图片预览


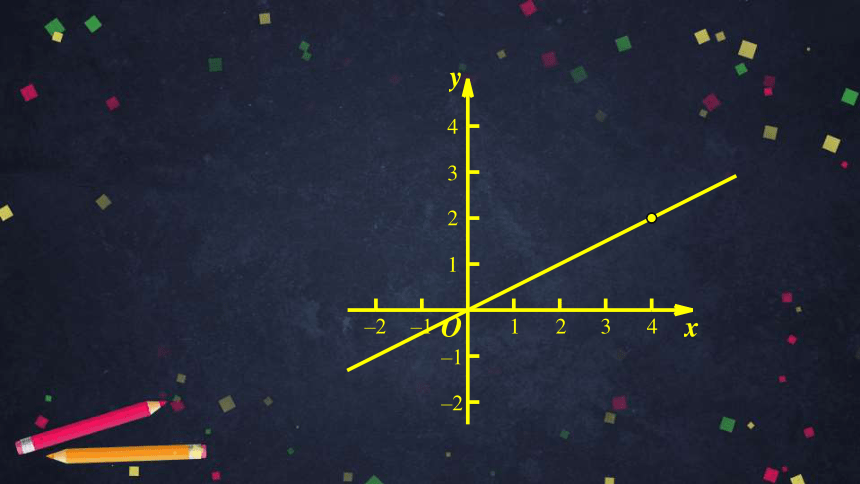



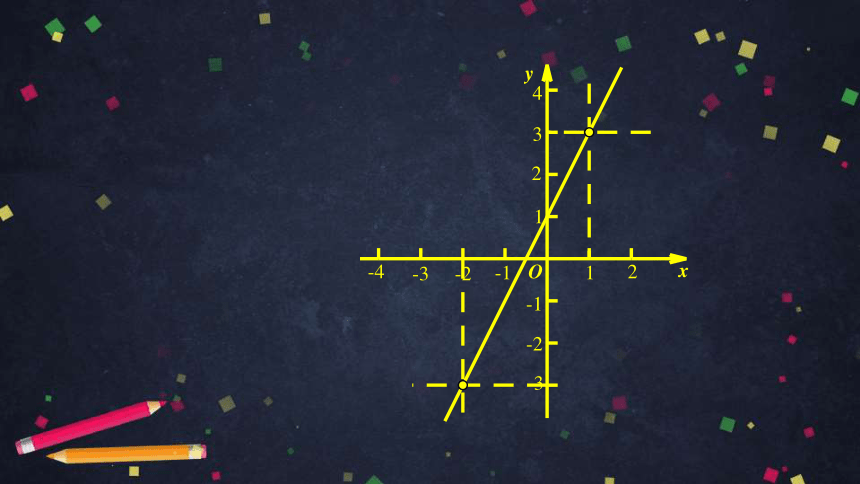

文档简介
(共40张PPT)
一次函数的图象(第二课时)
初二年级 数学
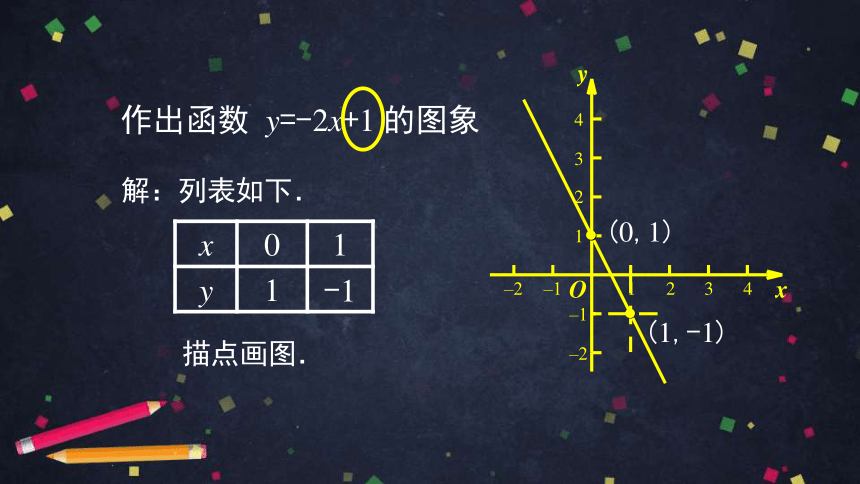
作出函数 y=-2x+1 的图象
x 0 1
y 1 -1
解:列表如下.
描点画图.
(0,1)
(1,-1)
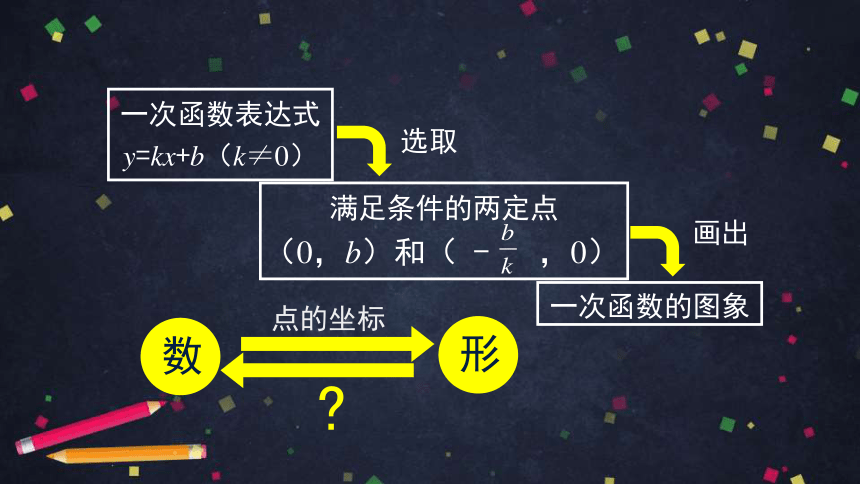
一次函数表达式
y=kx+b(k≠0)
满足条件的两定点
(0,b)和( - ,0)
一次函数的图象
选取
画出
数
形
?
点的坐标
A(4,2)
正比例函数的图象经过点A(4,2),求这个正比例函数的表达式.
探究:正比例函数的图象经过点A(4,2),
求这个正比例函数的表达式.
y=kx(k≠0)
解:设这个正比例函数的表达式为 y=kx (k≠0),
由于点A(4,2)在这个正比例函数图象上,
所以有 4k=2,解得 k = .
正比例函数的表达式为: y = x .
探究:正比例函数的图象经过点A(4,2),
求这个正比例函数的表达式.
一次函数的图象经过点
A(-2,-3),B(1,3),
求这个一次函数表达式.
探究:已知一次函数的图象经过A(-2,-3),
B(1,3),求这个一次函数的表达式.
y=kx+b(k≠0)
解:
设这个一次函数的表达式为y=kx+b(k≠0)
由于点A(-2,-3),B(1,3)在这个一
次函数图象上,所以有
-2k+b=-3
k+b=3
探究:已知一次函数的图象经过A(-2,-3),
B(1,3),求这个一次函数的表达式.
解:
探究:已知一次函数的图象经过A(-2,-3),
B(1,3),求这个一次函数的表达式.
k=2
b=1
解这个二元一次方程组,得
于是,得到这个一次函数表达式为
y =2x+1
步骤梳理:
1.设这个一次函数的表达式为
y=kx+b(k≠0);
2.根据已知条件列出关于k、b的二元
一次方程组;
3.解这个方程组,求出k,b的值;
4.将求出k,b的值代入表达式.
先把所求的系数设为未知数,再根据所给的条件确定这些系数的方法,叫做待定系数法,它是确定函数表达式时的一种常用方法.
解:
设这个一次函数的表达式为y=kx+b(k≠0)
由于点(-3,5),(5,9)在这个一次
函数图象上,所以有
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
-3k+b=5
5k+b=9
解这个二元一次方程组,得
k=
b=
解:
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
解:
于是,得到这个一次函数表达式为
y= x + .
令x=0,得y= ;令y=0,得x=-13.
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
(0,)
(-13,0)
解:
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
②求m的值;
③检验点(10,-8)是否在图象上.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
设这个一次函数的表达式为y=kx+b(k≠0)
由于点A(2,0),B(0,2)在函数的图
象上,所以有
2k+b=0
b=2
解:
解这个二元一次方程组得
k =-1
b=2
函数表达式为:
y=-x+2
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
解:
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
②求m的值;
y=-x+2
由于点C(m,3)在函数图象上,于是有
-m+2=3,
解得m=-1.
解:
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
②求m的值;
③检验点(10,-8)是否在图象上.
解:把x=10代入 y=-x+2 中,y=-8.
所以点(10,-8)在图象上.
y=-x+2
已知:平面直角坐标系中A(2,0),
B(0,2),C(m,3)三点共线,求m的值.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
求证:平面直角坐标系中A(2,0),
B(0,2),C(-1,3)三点共线.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
A
解:
点B的坐标为B1(-6,0),B2(6,0).
B2(6,0)
A
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
B1(-6,0)
设一次函数图象与x轴交于点B
∵S△AOB = OA·OB
∴ = 6
设直线AB1的表达式为y=kx+b(k≠0)
由于点(0,3),
(-6,0)在这个一次函数图象上
B1(-6,0)
B2(6,0)
A
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
解:
-6k+b=0
b=3
∴直线AB1的表达式为
同理可知直线AB2的
表达式为y=- x+3.
k=
b=3
y= x+3
解得
B1(-6,0)
B2(6,0)
A
解:
A
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
挑战一下:
1.已知一次函数y=kx+b,当x=1时,y=-2,且其图象与y轴交点的纵坐标为-5,则其表达为 .
(0,-5)
-5
把x=1时,y=-2代入 y=kx-5中得
k -5=-2,解得 k =3
y=3x-5
(1,-2)
挑战一下:
2.已知直线y=kx+b经过点(2,0),且与坐标轴所围成的三角形的面积为6. 求该直线的表达式.
y=-3x+6
y=3x-6
一次函数表达式
y=kx+b(k≠0)
满足条件的两定点
(0,b)和( - ,0)
一次函数的图象
选取
画出
选取
解出
待定系数法
数
形
点的坐标
一次函数的表达式
一次函数的图象
作业: 一次函数的图象经过点A(2,5)和x轴上一点B,且点B的横坐标为-3,求这个一次函数表达式.
且点B到坐标原点的距离为3
同学们,只要你善于观察,你一定能从数学学习中找到乐趣, 祝大家每天都有新的发现,新的收获.
一次函数的图象(第二课时)
初二年级 数学
作出函数 y=-2x+1 的图象
x 0 1
y 1 -1
解:列表如下.
描点画图.
(0,1)
(1,-1)
一次函数表达式
y=kx+b(k≠0)
满足条件的两定点
(0,b)和( - ,0)
一次函数的图象
选取
画出
数
形
?
点的坐标
A(4,2)
正比例函数的图象经过点A(4,2),求这个正比例函数的表达式.
探究:正比例函数的图象经过点A(4,2),
求这个正比例函数的表达式.
y=kx(k≠0)
解:设这个正比例函数的表达式为 y=kx (k≠0),
由于点A(4,2)在这个正比例函数图象上,
所以有 4k=2,解得 k = .
正比例函数的表达式为: y = x .
探究:正比例函数的图象经过点A(4,2),
求这个正比例函数的表达式.
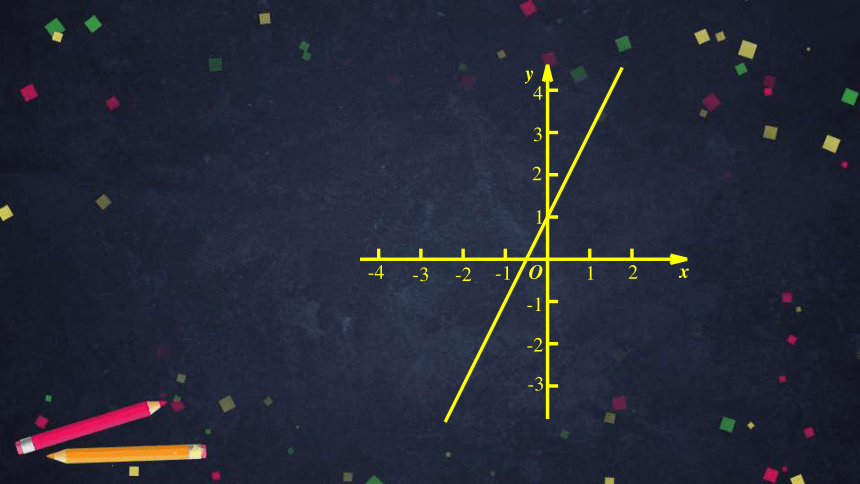
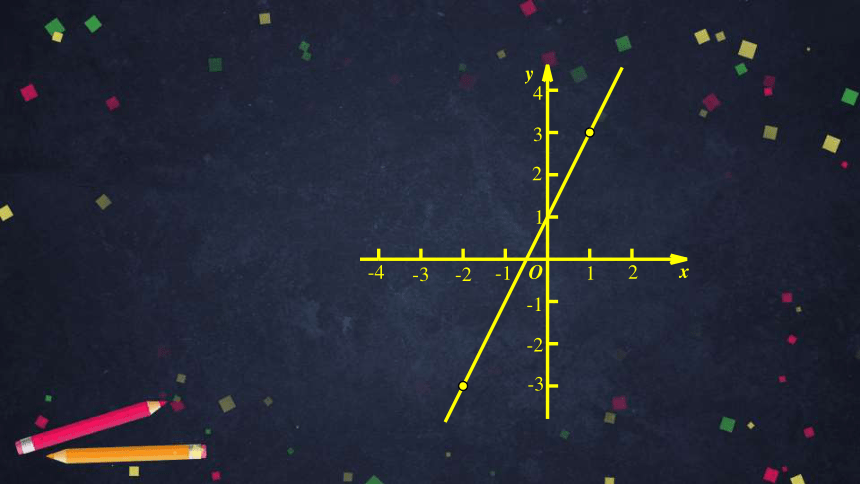
一次函数的图象经过点
A(-2,-3),B(1,3),
求这个一次函数表达式.
探究:已知一次函数的图象经过A(-2,-3),
B(1,3),求这个一次函数的表达式.
y=kx+b(k≠0)
解:
设这个一次函数的表达式为y=kx+b(k≠0)
由于点A(-2,-3),B(1,3)在这个一
次函数图象上,所以有
-2k+b=-3
k+b=3
探究:已知一次函数的图象经过A(-2,-3),
B(1,3),求这个一次函数的表达式.
解:
探究:已知一次函数的图象经过A(-2,-3),
B(1,3),求这个一次函数的表达式.
k=2
b=1
解这个二元一次方程组,得
于是,得到这个一次函数表达式为
y =2x+1
步骤梳理:
1.设这个一次函数的表达式为
y=kx+b(k≠0);
2.根据已知条件列出关于k、b的二元
一次方程组;
3.解这个方程组,求出k,b的值;
4.将求出k,b的值代入表达式.
先把所求的系数设为未知数,再根据所给的条件确定这些系数的方法,叫做待定系数法,它是确定函数表达式时的一种常用方法.
解:
设这个一次函数的表达式为y=kx+b(k≠0)
由于点(-3,5),(5,9)在这个一次
函数图象上,所以有
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
-3k+b=5
5k+b=9
解这个二元一次方程组,得
k=
b=
解:
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
解:
于是,得到这个一次函数表达式为
y= x + .
令x=0,得y= ;令y=0,得x=-13.
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
(0,)
(-13,0)
解:
例1 一个一次函数的图象经过(-3,5)和
(5,9)两点,求它和坐标轴交点的坐标.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
②求m的值;
③检验点(10,-8)是否在图象上.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
设这个一次函数的表达式为y=kx+b(k≠0)
由于点A(2,0),B(0,2)在函数的图
象上,所以有
2k+b=0
b=2
解:
解这个二元一次方程组得
k =-1
b=2
函数表达式为:
y=-x+2
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
解:
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
②求m的值;
y=-x+2
由于点C(m,3)在函数图象上,于是有
-m+2=3,
解得m=-1.
解:
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
①求这个函数的表达式;
②求m的值;
③检验点(10,-8)是否在图象上.
解:把x=10代入 y=-x+2 中,y=-8.
所以点(10,-8)在图象上.
y=-x+2
已知:平面直角坐标系中A(2,0),
B(0,2),C(m,3)三点共线,求m的值.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
求证:平面直角坐标系中A(2,0),
B(0,2),C(-1,3)三点共线.
例2.一次函数y =kx+b的图象经过三点
A(2,0),B(0,2),C(m,3).
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
A
解:
点B的坐标为B1(-6,0),B2(6,0).
B2(6,0)
A
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
B1(-6,0)
设一次函数图象与x轴交于点B
∵S△AOB = OA·OB
∴ = 6
设直线AB1的表达式为y=kx+b(k≠0)
由于点(0,3),
(-6,0)在这个一次函数图象上
B1(-6,0)
B2(6,0)
A
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
解:
-6k+b=0
b=3
∴直线AB1的表达式为
同理可知直线AB2的
表达式为y=- x+3.
k=
b=3
y= x+3
解得
B1(-6,0)
B2(6,0)
A
解:
A
例3 若一次函数y=kx+b的图象经过点 A(0,3),且与坐标轴围成的三角形面积为9.
求这个一次函数的表达式.
挑战一下:
1.已知一次函数y=kx+b,当x=1时,y=-2,且其图象与y轴交点的纵坐标为-5,则其表达为 .
(0,-5)
-5
把x=1时,y=-2代入 y=kx-5中得
k -5=-2,解得 k =3
y=3x-5
(1,-2)
挑战一下:
2.已知直线y=kx+b经过点(2,0),且与坐标轴所围成的三角形的面积为6. 求该直线的表达式.
y=-3x+6
y=3x-6
一次函数表达式
y=kx+b(k≠0)
满足条件的两定点
(0,b)和( - ,0)
一次函数的图象
选取
画出
选取
解出
待定系数法
数
形
点的坐标
一次函数的表达式
一次函数的图象
作业: 一次函数的图象经过点A(2,5)和x轴上一点B,且点B的横坐标为-3,求这个一次函数表达式.
且点B到坐标原点的距离为3
同学们,只要你善于观察,你一定能从数学学习中找到乐趣, 祝大家每天都有新的发现,新的收获.
同课章节目录
