北京版八年级下册数学课件:14.7 一次函数的应用(第一课时)(80张ppt)
文档属性
| 名称 | 北京版八年级下册数学课件:14.7 一次函数的应用(第一课时)(80张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 00:00:00 | ||
图片预览









文档简介
(共80张PPT)
初二年级 数学
一次函数的应用(第一课时)
数学知识
数学知识
其它学科
生产生活
一次函数
实际问题
数学知识
实际问题
数学问题
数学问题的解
实际问题的解
一次函数
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
三角形周长等于三边之和
等腰三角形两腰相等
周长=底 + 腰×2
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
三角形周长等于三边之和
等腰三角形两腰相等
原来周长=12+10×2=32
周长=底 + 腰×2
12
10
10
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
三角形周长等于三边之和
等腰三角形两腰相等
周长=底 + 腰×2
12×2
10+x
y=12×2+(10+x)×2
y=2x+44
10+x
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
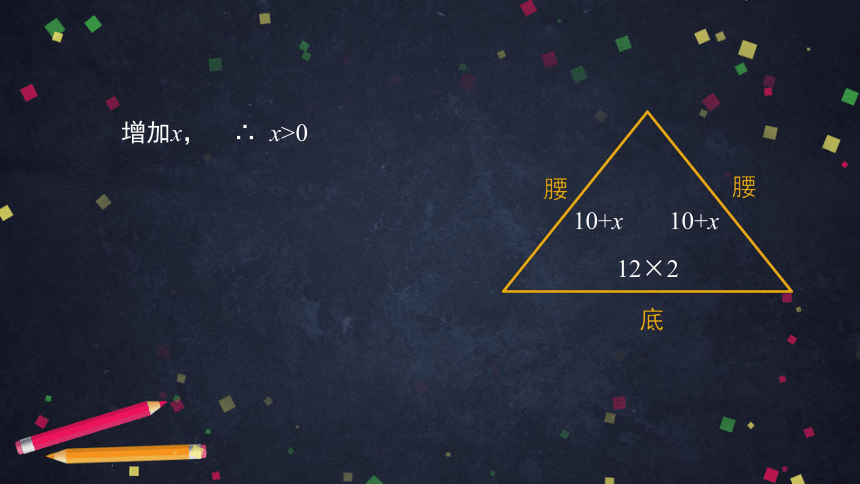
增加x, ∴ x>0
12×2
10+x
10+x
增加x, ∴ x>0
三角形两边之和大于第三边
12×2
10+x
10+x
增加x, ∴ x>0
三角形两边之和大于第三边
12×2
10+x
10+x
∴(10+x)×2>12×2
增加x, ∴ x>0
三角形两边之和大于第三边
∴(10+x)×2>12×2
解得, x>2
12×2
10+x
10+x
增加x, ∴ x>0
三角形两边之和大于第三边
∴(10+x)×2>12×2
解得, x>2
12×2
10+x
10+x
∴ x>2
自变量的取值范围为x>2.
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(2)求当x为何值时,周长y变为原来的3倍.
三角形周长等于三边之和
等腰三角形两腰相等
原来周长=12+10×2=32
周长=底 + 腰×2
12
10
10
解:依题意得
y=32×3=96,
2x+44=96,
x=26.
答:当x为26时,周长变为原来的3倍.
把y=96代入y=2x+44中,得
解得
小结
1.根据问题的数量关系求函数表达式;
2.根据实际问题的意义求自变量的取值范围;
3.函数与方程有着密切联系.
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(1)写出购买这种化肥的总金额M(元)与购买袋数n的函数表达式,并指出它的自变量的取值范围;
总金额 单价 袋数
0≤n≤3
n≥4
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(1)写出购买这种化肥的总金额M(元)与购买袋数n的函数表达式,并指出它的自变量的取值范围;
0≤n≤3
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(1)写出购买这种化肥的总金额M(元)与购买袋数n的函数表达式,并指出它的自变量的取值范围;
80(1-5%)
n≥4
单价80
单价
80(1-5%)
n 1 2 3 4 5
M(元)
80
160
240
n(n≥4)
80(1-5%)=76
n=4
每袋80元
每袋76元
80×3=240
76
240+76=316
n 1 2 3 4 5
M(元)
80
160
240
316
80(1-5%)=76
n(n≥4)
n=5
每袋80元
每袋76元
76×2
240+76×2=392
80×3=240
n 1 2 3 4 5
M(元)
80
160
240
316
392
80(1-5%)=76
n(n≥4)
……
n(n≥4)
每袋80元
每袋76元
80×3=240
76×(n-3)
…
240+76(n-3)=76n+12
n 1 2 3 4 5
M(元)
80
160
240
316
392
76n+12
80(1-5%)=76
n(n≥4)
解(1):当0≤n≤3时,函数的表达式为 M=80n.
自变量n的取值范围是0≤n≤3且n是整数.
当n≥4时, 函数的表达式为
M=76n+12.
自变量n的取值范围是n≥4且n是整数.
,0≤n≤3且n是整数,
,n≥4且n是整数.
变式:某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,买4袋及以上,每袋优惠5%.
每袋80元
80×3=240
变式:某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,买4袋及以上,每袋优惠5%.
每袋76元
76×4=304
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(2)为了快速得到购买这种化肥的总金额,利用这个函数的表达式制作一个购买1~10袋化肥的总金额对照表.
n 1 2 3 4 5
M(元)
80
160
240
316
392
76n+12
(2)当n依次取1~10时,分别计算出函数的值,得出下表:
n(n≥4)
解(1):当0≤n≤3时,函数的表达式为 M=80n.
自变量n的取值范围是0≤n≤3且n是整数.
当n≥4时, 函数的表达式为
M=76n+12.
自变量n的取值范围是n≥4且n是整数.
n 6 7 8 9 10
M(元) 468 544 620 696 772
n 1 2 3 4 5
M(元)
80
160
240
316
392
76n+12
(2)当n依次取1~10时,分别计算出函数的值,得出下表:
n(n≥4)
小结
1.分段(计价)问题要分段处理;
2.要写出每段中自变量的取值范围;
3.对于给定自变量的值要判断在哪一段,在哪一段,就用这一段对应的函数表达式解决.
思考:如果给定的是函数值呢?
练习1.北京居民用水价按家庭年用水量计算,标准如下:
第一阶梯上限180立方米,水费价格为5元/立方米;
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
(1)请列出y关于x的函数表达式,并写出自变量的取值范围;
180<200<260
180
20
5×
×7
第一阶梯上限180立方米,水费为5元/立方米;
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
当0≤x≤180时,y=5x
0≤x≤180
第一阶梯上限180立方米,水费为5元/立方米;
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
180第二阶梯为180以上至260立方米,水费价格为7元/立方米;
180×5,
前180立方米的水费为
(x-180)×7,
180立方米以后的水费为
y=180×5+(x-180)×7.
y=7x-360.
当180第一阶梯上限180立方米,水费为5元/立方米;
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
x>260
第三阶梯为260立方米,水费价格为9元/立方米.
前180立方米的水费为 180×5,
180到260立方米的水费为 (260-180)×7,
260立方米以后的水费为 (x-260)×9,
y=180×5+(260-180)×7+(x-260)×9.
y=9x-880.
当x≥260时,
当0≤x≤180时,
y=5x.
当180y=7x-360.
当x>260时,
y=9x-880.
(2)某户去年缴纳水费1145元,该户去年用水量是多少?
当0≤x≤180时,
y=5x.
当180y=7x-360.
当x>260时,
y=9x-880.
5×180=900
7×260-360=1460
0≤y≤900.
900y>1460.
(2)某户去年缴纳水费1145元,该户去年用水量是多少?
所以把y=1145代入y=7x-360中,得
因为900<1145<1460,
1145=7x-360.
解得 x=215.
答:该户去年用水量为215立方米.
小结
如果给定分段函数的函数值,应先判断是哪段的函数值,再代入那一段求解.
思考:会不会出现已知函数值在多个阶段呢?
有没有更简洁的判断方法?
例3.某工厂每天生产A,B两种品牌的零件共600件.A,B两种零件的成本及利润如下表.设每天生产A种零件x件,每天获利y元.
A B
成本(元/件) 50 35
利润(元/件) 20 15
(1)请写出y与x的函数表达式;
A种零件的总利润
y=
B种零件的总利润
+
y=A种零件的总利润+B种零件的总利润
单件利润×件数
单件利润×件数
20
15
x
?
例3.某工厂每天生产A,B两种品牌的零件共600件.A,B两种零件的成本及利润如下表.设每天生产A种零件x件,每天获利y元.
x
600-x
A B
成本(元/件) 50 35
利润(元/件) 20 15
y=A种零件的总利润+B种零件的总利润
单件利润×件数
单件利润×件数
20
15
x
?
(600-x)
y=20x+15×(600-x),
y=5x+9000.
0≤x≤600,且x是整数.
(2)如果该零件厂每天投入成本27000元,那么每天获利多少元?
y=5x+9000.
x=?
A B
成本(元/件) 50 35
利润(元/件) 20 15
27000=A种零件的总成本+B种零件的总成本
单件成本×件数
50
35
27000=50x+35×(600-x)
单件成本×件数
x
(600-x)
解:依题意得
27000=50x+35×(600-x),
解得 x=400,
y=5×400+9000=11000.
代入得
答:如果每天投入成本27000元,每天获利11000元.
A B
成本(元/件) 50 35
利润(元/件) 20 15
x≥200
600-x≥200
(3)如果每天生产的两种零件都不少于200件,该厂应如何安排生产才能获利最大,最大利润是多少?
200≤x≤400
A B
成本(元/件) 50 35
利润(元/件) 20 15
y=5x+9000,
(3)如果每天生产的两种零件都不少于200件,该厂应如何安排生产才能获利最大,最大利润是多少?
复习一次函数的性质
一次函数y=kx+b(k≠0)的性质是:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
对于一次函数y=5x+9000,
由于 k=5>0,
所以y的值随x的增大而增大,
当x取最大值400时,y有最大值,
答:每天生产A种零件400件,B种零件200件时利润最大,最大利润为11000元.
最大值是5×400+9000=11000.
小结
1.条件较多时要聚焦相关条件;
2.通过一次函数的性质可以解决一些最大值(或最小值)问题,应用时要确定自变量的取值范围.
变式:某工厂每天生产A,B两种品牌的零件共600件.A,B两种零件的成本及利润如下表.设每天生产B种零件x件,每天获利y元.
A B
成本(元/件) 50 35
利润(元/件) 20 15
600-x
x
(1)请写出y与x的函数表达式;
(3)如果每天生产的两种零件都不少于200件,该厂应如何安排生产才能获利最大,最大利润是多少?
A B
成本(元/件) 50 35
利润(元/件) 20 15
y=A种零件的总利润+B种零件的总利润
单件利润×件数
单件利润×件数
20 (600-x)
15 x
y=20(600-x)+15x
y=-5x+12000.
y=20(600-x)+15x
解(1):由题意得
化简得
600-x≥200
解(3):依题意有
解得
x≥200
200≤x≤400
对于一次函数y=-5x+12000,
由于k= -5<0,
所以y的值随x的增大而减小.
当x取最小值200时,y有最大值,
答:每天生产A种零件400件,B种零件200件时利润最大,最大利润为11000元.
最大值是-5×200+12000=11000.
总结
本节课我们解决了以下几个具体问题:
等腰三角形的周长;
降价销售;
阶梯水价;
生产安排.
总结
本节课我们遇到了以下几个一次函数问题:
根据题目条件列出一次函数(含分段函数)表达式;
根据实际问题的意义确定自变量的取值范围;
求给定条件的函数值;
求给定条件的函数的最大值.
总结
应用一次函数解决问题要注意以下几点:
注意变量的实际意义;
分段函数要分段处理;
利用函数性质求最大值时要确定自变量的取值范围;
对于复杂的题目条件要聚焦相关条件.
作业
课本本节练习第2题和本章复习题提升部分第4题
作业
祝同学们学有所成
初二年级 数学
一次函数的应用(第一课时)
数学知识
数学知识
其它学科
生产生活
一次函数
实际问题
数学知识
实际问题
数学问题
数学问题的解
实际问题的解
一次函数
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
三角形周长等于三边之和
等腰三角形两腰相等
周长=底 + 腰×2
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
三角形周长等于三边之和
等腰三角形两腰相等
原来周长=12+10×2=32
周长=底 + 腰×2
12
10
10
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
三角形周长等于三边之和
等腰三角形两腰相等
周长=底 + 腰×2
12×2
10+x
y=12×2+(10+x)×2
y=2x+44
10+x
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(1)列出现在三角形周长y与x的函数表达式,并指出自变量的取值范围.
增加x, ∴ x>0
12×2
10+x
10+x
增加x, ∴ x>0
三角形两边之和大于第三边
12×2
10+x
10+x
增加x, ∴ x>0
三角形两边之和大于第三边
12×2
10+x
10+x
∴(10+x)×2>12×2
增加x, ∴ x>0
三角形两边之和大于第三边
∴(10+x)×2>12×2
解得, x>2
12×2
10+x
10+x
增加x, ∴ x>0
三角形两边之和大于第三边
∴(10+x)×2>12×2
解得, x>2
12×2
10+x
10+x
∴ x>2
自变量的取值范围为x>2.
例1.已知等腰三角形的腰长为10,底边长为12,现将底边长变为原来的2倍,腰长增加x.
(2)求当x为何值时,周长y变为原来的3倍.
三角形周长等于三边之和
等腰三角形两腰相等
原来周长=12+10×2=32
周长=底 + 腰×2
12
10
10
解:依题意得
y=32×3=96,
2x+44=96,
x=26.
答:当x为26时,周长变为原来的3倍.
把y=96代入y=2x+44中,得
解得
小结
1.根据问题的数量关系求函数表达式;
2.根据实际问题的意义求自变量的取值范围;
3.函数与方程有着密切联系.
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(1)写出购买这种化肥的总金额M(元)与购买袋数n的函数表达式,并指出它的自变量的取值范围;
总金额 单价 袋数
0≤n≤3
n≥4
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(1)写出购买这种化肥的总金额M(元)与购买袋数n的函数表达式,并指出它的自变量的取值范围;
0≤n≤3
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(1)写出购买这种化肥的总金额M(元)与购买袋数n的函数表达式,并指出它的自变量的取值范围;
80(1-5%)
n≥4
单价80
单价
80(1-5%)
n 1 2 3 4 5
M(元)
80
160
240
n(n≥4)
80(1-5%)=76
n=4
每袋80元
每袋76元
80×3=240
76
240+76=316
n 1 2 3 4 5
M(元)
80
160
240
316
80(1-5%)=76
n(n≥4)
n=5
每袋80元
每袋76元
76×2
240+76×2=392
80×3=240
n 1 2 3 4 5
M(元)
80
160
240
316
392
80(1-5%)=76
n(n≥4)
……
n(n≥4)
每袋80元
每袋76元
80×3=240
76×(n-3)
…
240+76(n-3)=76n+12
n 1 2 3 4 5
M(元)
80
160
240
316
392
76n+12
80(1-5%)=76
n(n≥4)
解(1):当0≤n≤3时,函数的表达式为 M=80n.
自变量n的取值范围是0≤n≤3且n是整数.
当n≥4时, 函数的表达式为
M=76n+12.
自变量n的取值范围是n≥4且n是整数.
,0≤n≤3且n是整数,
,n≥4且n是整数.
变式:某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,买4袋及以上,每袋优惠5%.
每袋80元
80×3=240
变式:某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,买4袋及以上,每袋优惠5%.
每袋76元
76×4=304
例2.某生产资料门市部出售化肥,每袋售价80元.为了促进销售,规定了优惠办法:买3袋按售价计算,从第4袋开始,每袋优惠5%.
(2)为了快速得到购买这种化肥的总金额,利用这个函数的表达式制作一个购买1~10袋化肥的总金额对照表.
n 1 2 3 4 5
M(元)
80
160
240
316
392
76n+12
(2)当n依次取1~10时,分别计算出函数的值,得出下表:
n(n≥4)
解(1):当0≤n≤3时,函数的表达式为 M=80n.
自变量n的取值范围是0≤n≤3且n是整数.
当n≥4时, 函数的表达式为
M=76n+12.
自变量n的取值范围是n≥4且n是整数.
n 6 7 8 9 10
M(元) 468 544 620 696 772
n 1 2 3 4 5
M(元)
80
160
240
316
392
76n+12
(2)当n依次取1~10时,分别计算出函数的值,得出下表:
n(n≥4)
小结
1.分段(计价)问题要分段处理;
2.要写出每段中自变量的取值范围;
3.对于给定自变量的值要判断在哪一段,在哪一段,就用这一段对应的函数表达式解决.
思考:如果给定的是函数值呢?
练习1.北京居民用水价按家庭年用水量计算,标准如下:
第一阶梯上限180立方米,水费价格为5元/立方米;
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
(1)请列出y关于x的函数表达式,并写出自变量的取值范围;
180<200<260
180
20
5×
×7
第一阶梯上限180立方米,水费为5元/立方米;
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
当0≤x≤180时,y=5x
0≤x≤180
第一阶梯上限180立方米,水费为5元/立方米;
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
180
180×5,
前180立方米的水费为
(x-180)×7,
180立方米以后的水费为
y=180×5+(x-180)×7.
y=7x-360.
当180
第二阶梯为180以上至260立方米,水费价格为7元/立方米;
第三阶梯为260立方米以上,水费价格为9元/立方米.
设家庭年用水量x立方米,年水费y元.
x>260
第三阶梯为260立方米,水费价格为9元/立方米.
前180立方米的水费为 180×5,
180到260立方米的水费为 (260-180)×7,
260立方米以后的水费为 (x-260)×9,
y=180×5+(260-180)×7+(x-260)×9.
y=9x-880.
当x≥260时,
当0≤x≤180时,
y=5x.
当180
当x>260时,
y=9x-880.
(2)某户去年缴纳水费1145元,该户去年用水量是多少?
当0≤x≤180时,
y=5x.
当180
当x>260时,
y=9x-880.
5×180=900
7×260-360=1460
0≤y≤900.
900
(2)某户去年缴纳水费1145元,该户去年用水量是多少?
所以把y=1145代入y=7x-360中,得
因为900<1145<1460,
1145=7x-360.
解得 x=215.
答:该户去年用水量为215立方米.
小结
如果给定分段函数的函数值,应先判断是哪段的函数值,再代入那一段求解.
思考:会不会出现已知函数值在多个阶段呢?
有没有更简洁的判断方法?
例3.某工厂每天生产A,B两种品牌的零件共600件.A,B两种零件的成本及利润如下表.设每天生产A种零件x件,每天获利y元.
A B
成本(元/件) 50 35
利润(元/件) 20 15
(1)请写出y与x的函数表达式;
A种零件的总利润
y=
B种零件的总利润
+
y=A种零件的总利润+B种零件的总利润
单件利润×件数
单件利润×件数
20
15
x
?
例3.某工厂每天生产A,B两种品牌的零件共600件.A,B两种零件的成本及利润如下表.设每天生产A种零件x件,每天获利y元.
x
600-x
A B
成本(元/件) 50 35
利润(元/件) 20 15
y=A种零件的总利润+B种零件的总利润
单件利润×件数
单件利润×件数
20
15
x
?
(600-x)
y=20x+15×(600-x),
y=5x+9000.
0≤x≤600,且x是整数.
(2)如果该零件厂每天投入成本27000元,那么每天获利多少元?
y=5x+9000.
x=?
A B
成本(元/件) 50 35
利润(元/件) 20 15
27000=A种零件的总成本+B种零件的总成本
单件成本×件数
50
35
27000=50x+35×(600-x)
单件成本×件数
x
(600-x)
解:依题意得
27000=50x+35×(600-x),
解得 x=400,
y=5×400+9000=11000.
代入得
答:如果每天投入成本27000元,每天获利11000元.
A B
成本(元/件) 50 35
利润(元/件) 20 15
x≥200
600-x≥200
(3)如果每天生产的两种零件都不少于200件,该厂应如何安排生产才能获利最大,最大利润是多少?
200≤x≤400
A B
成本(元/件) 50 35
利润(元/件) 20 15
y=5x+9000,
(3)如果每天生产的两种零件都不少于200件,该厂应如何安排生产才能获利最大,最大利润是多少?
复习一次函数的性质
一次函数y=kx+b(k≠0)的性质是:
当k>0时,y随x的增大而增大;
当k<0时,y随x的增大而减小.
对于一次函数y=5x+9000,
由于 k=5>0,
所以y的值随x的增大而增大,
当x取最大值400时,y有最大值,
答:每天生产A种零件400件,B种零件200件时利润最大,最大利润为11000元.
最大值是5×400+9000=11000.
小结
1.条件较多时要聚焦相关条件;
2.通过一次函数的性质可以解决一些最大值(或最小值)问题,应用时要确定自变量的取值范围.
变式:某工厂每天生产A,B两种品牌的零件共600件.A,B两种零件的成本及利润如下表.设每天生产B种零件x件,每天获利y元.
A B
成本(元/件) 50 35
利润(元/件) 20 15
600-x
x
(1)请写出y与x的函数表达式;
(3)如果每天生产的两种零件都不少于200件,该厂应如何安排生产才能获利最大,最大利润是多少?
A B
成本(元/件) 50 35
利润(元/件) 20 15
y=A种零件的总利润+B种零件的总利润
单件利润×件数
单件利润×件数
20 (600-x)
15 x
y=20(600-x)+15x
y=-5x+12000.
y=20(600-x)+15x
解(1):由题意得
化简得
600-x≥200
解(3):依题意有
解得
x≥200
200≤x≤400
对于一次函数y=-5x+12000,
由于k= -5<0,
所以y的值随x的增大而减小.
当x取最小值200时,y有最大值,
答:每天生产A种零件400件,B种零件200件时利润最大,最大利润为11000元.
最大值是-5×200+12000=11000.
总结
本节课我们解决了以下几个具体问题:
等腰三角形的周长;
降价销售;
阶梯水价;
生产安排.
总结
本节课我们遇到了以下几个一次函数问题:
根据题目条件列出一次函数(含分段函数)表达式;
根据实际问题的意义确定自变量的取值范围;
求给定条件的函数值;
求给定条件的函数的最大值.
总结
应用一次函数解决问题要注意以下几点:
注意变量的实际意义;
分段函数要分段处理;
利用函数性质求最大值时要确定自变量的取值范围;
对于复杂的题目条件要聚焦相关条件.
作业
课本本节练习第2题和本章复习题提升部分第4题
作业
祝同学们学有所成
同课章节目录
