北京版八年级下册数学课件:14.4一次函数的概念 (第一课时)(62张ppt)
文档属性
| 名称 | 北京版八年级下册数学课件:14.4一次函数的概念 (第一课时)(62张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 18:52:52 | ||
图片预览










文档简介
(共62张PPT)
初二年级 数学
一次函数的概念 (第一课时)
函数
特殊函数
函数的定义
函数的表示方法
函数图象的画法
一般到特殊
{
判断下列每个问题中的两个变量是否构成函数关系.如果是,指出哪一个是自变量,哪一个是因变量,并分别写出每一个函数表达式:
交流
1. 一个长方形的一边长是 3 cm,它的面积
S(cm?)和另一边的长 m(cm)对应.
示意图:
3cm
m
S
分析:(1)在这个问题中存在哪两个变量?
S 和 m
示意图:
3cm
m
S
m ? cm
S ? cm?
3
1
2
3
4
9
6
12
…
…
…
…
分析:(2)它们之间存在函数关系吗?
S 是m 的函数,m 是自变量,S 是因变量.
示意图:
3cm
m
S
分析:(3)你能写出这个函数的表达式吗?
S=3m
(m > 0)
小结:
1.画出示意图,在图上标注已知条件,找到两个变量.
2.通过列表计算分析两个变量之间是否存在函数关系.
3.列函数表达式,确定自变量的取值范围.
2.正方形的面积 S 与它的边长 a 对应.
示意图:
分析:(1)在这个问题中存在哪两个变量?
S 和 a
a
S
示意图:
分析:(2)它们之间存在函数关系吗?
S 是 a 的函数,
a 是自变量,S 是因变量
1
1
2
2
4
3
9
a
S
…
…
…
…
a
S
示意图:
a
S
S = a?
(a > 0)
分析:(3)你能写出这个函数的表达式吗?
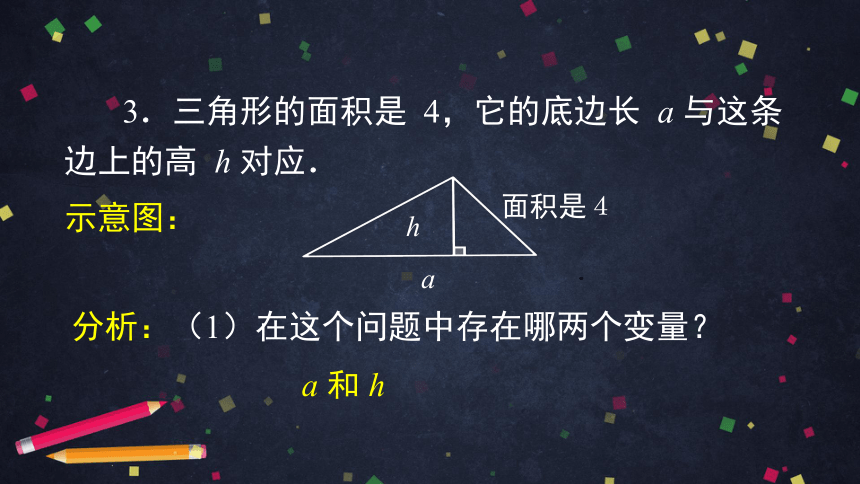
3.三角形的面积是 4,它的底边长 a 与这条
边上的高 h 对应.
示意图:
a 和 h
分析:(1)在这个问题中存在哪两个变量?
a
h
面积是4
示意图:
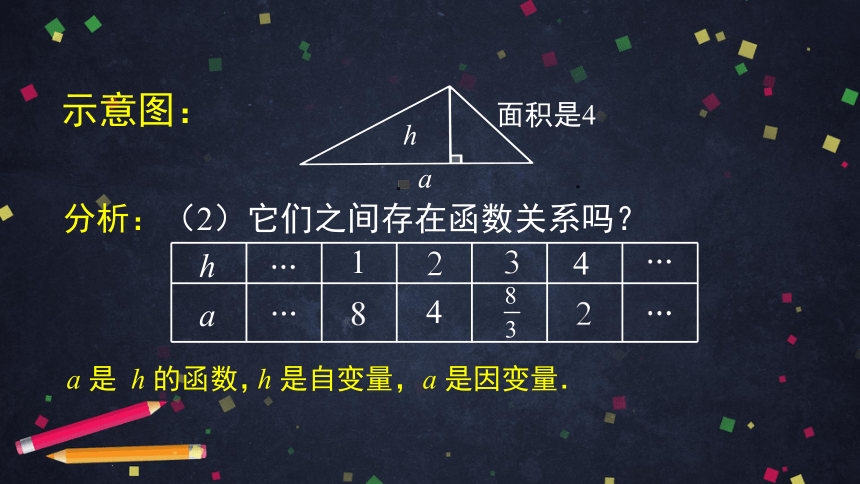
分析:(2)它们之间存在函数关系吗?
a 是 h 的函数,
h 是自变量,a 是因变量.
a
h
面积是4
1
8
2
4
3
4
2
…
…
…
…
a
h
示意图:
a
h
面积是4
分析:(3)你能写出这个函数的表达式吗?
(h>0)
4.等腰三角形顶角的度数 α 和它的一个底角的度数 β 对应.
示意图:
分析:(1)在这个问题中存在哪两个变量?
α 和 β
示意图:
分析:(2)它们之间存在函数关系吗?
α 是 β 的函数,
β 是自变量,α 是因变量.
示意图:
分析:(3)你能写出这个函数的表达式吗?
α+2β =180
α =180 -2β
思考:你能求出自变量的取值范围吗?
分析:
α =180 -2β
180 -2β > 0
β < 90
所以自变量的取值范围是 0<β<90
β >0
α >0
{
β >0
{
β<90
示意图:
函数表达式: α =180 -2β
(0<β<90)
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
分析:最大量程为 5 N
即 p≤5
弹簧秤所能承受的最大物重为5 N
又因为 p≥0
所以 0≤p≤5
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
分析:原长度是15cm
即弹簧秤未挂重物时,它的自然长度是15 cm.
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
…
0.5
0.5+15
0.5×2
0.5×2+15
0.5×3
0.5×3+15
0.5×4
0.5×4+15
1
2
3
4
…
…
p
0.5p
物重
(p ? N )
伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
伸长长度
(cm)
总长度
(L ? cm)
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
伸长后弹簧的总长度 L(cm)是所称物重 p(N)的函数,其中 p 是自变量,L 是因变量.
…
0.5
0.5+15
0.5×2
0.5×2+15
0.5×3
0.5×3+15
0.5×4
0.5×4+15
1
2
3
4
…
…
p
0.5p
物重
(p ? N )
伸长长度
(cm)
总长度
(L ? cm)
你能写出这个函数的表达式吗?
…
0.5
0.5×1+15
0.5×2
0.5×2+15
0.5×3
0.5×3+15
0.5×4
0.5×4+15
1
2
3
4
…
…
p
0.5p
物重
(p ? N )
伸长长度
(cm)
总长度
(L ? cm)
你能写出这个函数的表达式吗?
0.5p+15
你能写出这个函数的表达式吗?
L =0.5p+15
思考:你能求出自变量的取值范围吗?
或L =15+0.5p
分析:最大量程为 5 N
即 p≤5
弹簧秤所能承受的最大物重为5 N
又因为 p≥0
所以0≤p≤5
函数的表达式:
(0≤p≤5)
L =0.5p+15
(1)S = 3m (2)S = a?
(3) (4)α =180 -2β
(5)L=0.5p+15
函数表达式:
3m ,a? , ,180 -2β ,0.5p+15
思考:你能将它们分类吗?分类的标准是什么?
a =
3m ,180 -2β , ,a? ,0.5p+15
关注
自变量的次数
自变量的系数
自变量的位置
有无常数项
3m ,180 -2β , ,a? ,0.5p+15
按自变量的
次数分类
二次
S =a?
一次
α =180-2β
S =3m
L =0.5p+15
{
负一次
a =
思考:等号右边含有自变量的代数式有什么共同的特征?
自变量的次数是1次
S =3m
a =180-2β
L =0.5p+15
一次函数
S =3m
a =180-2β
L =0.5p+15
思考:等号右边含有自变量的代数式的结构有什
么共同的特征?
右边:自变量与常数的积再加上常数项
a =-2β+180
加法交换律
S =3m
a =180-2β
L =0.5p+15
S =3m+0
右边:自变量与常数的积再加上常数项
S =3m
a =180-2β
L =0.5p+15
思考:你能用一个一般的函数表达式来概括这三
个表达式的结构特征吗?
y =kx +b(k,b为常数)
右边:自变量与常数的积再加上常数项
k
b
函数表达式:y = kx +b(k,b为常数)
思考:对于常数k的取值有限制吗?它可以为0吗?
所以k≠0,即自变量的系数不能为0
k =0时,
y =b ,
自变量的次数不是1次
函数表达式:y = kx +b(k,b为常数,且k≠0)
思考:对于常数k的取值有限制吗?它可以为0吗?
所以k≠0,即自变量的系数不能为0
k =0时,
y =b ,
自变量的次数不是1次
函数表达式:y = kx +b(k,b为常数,且k≠0)
思考:常数 b 的取值可以为0吗?
b= 0时, y = kx
(k为常数, k≠0)
正比例函数
一次函数:
一般地,我们把形如y =kx +b(k,b为常数,且k≠0)的函数叫做一次函数.其中 x 是自变量.
正比例函数:
当b=0时,一次函数y=kx(k≠0)又叫做正比
例函数.
思考:
一次函数y =kx +b(k,b是常数,且k≠0)自变量的取值范围是什么呢?
自变量的取值范围:全体实数
你能说说一次函数与正比例函数的关系吗?
一次函数包含正比例函数,
正比例函数是特殊的一次函数.
你能用一个图来表示它们之间的关系吗?
一次函数
正比例函数
例1 判断下列函数中,哪些是一次函数,一次函
数中哪些是正比例函数?
(5)
(1)
(2)
(3)
(4)
(6)
分析:
要想判断一个函数是否为一次函数,根据定义,只需判断函数表达式是否可以写成 y=kx +b(k,b为常数,且k≠0)的形式,即是否满足两个条件:(1)自变量的次数为1次,(2)自变量的系数不为0.
例1 判断下列函数中,哪些是一次函数,一次函
数中哪些是正比例函数?
(5)
(1)
(2)
(3)
(4)
(6)
例1 判断下列函数中,哪些是一次函数,一次函
数中哪些是正比例函数?
解:一次函数:
(1)
(2)
(4)
(6)
正比例函数:
(6)
(1)若它是一次函数,求 k 的值.
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(2)若它是正比例函数,求 k 的值.
分析:
{
自变量的次数为一次
k -2≠0
∴
k≠2
(1)若它是一次函数,求 k 的值.
自变量的系数不等于0
∴
自变量的系数
常数项
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(1)若它是一次函数,求 k 的值.
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
解:由题意得
k -2≠0
k≠2
∴
(2)若它是正比例函数,求 k 的值.
分析:
自变量的次数为一次
自变量的系数不等于0
常数项为0
{
自变量的系数
常数项
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(2)若它是正比例函数,求 k 的值.
k +1 0
k - 2 0
∴
k = -1
把k = -1代入k -2中,k - 2≠0成立
∴
分析:
k = -1
{
自变量的系数
常数项
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(2)若它是正比例函数,求 k 的值.
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
{
k +1= 0
k-2≠0
∴
k = -1
把k = -1代入k -2中,k - 2≠0成立
∴
k = -1
解:由题意得
例3 八年级一班学生接受了在公路的一边植50棵树的任务.树苗堆放在公路边的M处.现规定,第一棵树种在离点M3米远的A处,而且在MA的方向上每隔5米种一棵树 .那么每种一棵树苗时,送树苗所走的路程 S(米)是所种树苗的序号n 的函数.求出它的表达式,并求出它的自变量的取值范围.
分析:
50棵树
M
A
MA=3米
①
②
③
B
C
AB=BC=5米
分析:
50棵树
M
A
MA=3米
①
②
③
B
C
AB=BC=5米
n/棵
S/米
1
3
2
…
…
n
3
3+5×1
3+5×2
4
3+5×3
↓
3+5×0
S = 3+5(n -1)
自变量的取值范围是什么呢?
→
S =5n -2
n/棵
S/米
1
3
2
…
…
n
3
3+5×1
3+5×2
4
3+5×3
3+5(n -1)
例3 八年级一班学生接受了在公路的一边植50棵树的任务.树苗堆放在公路边的M处.现规定,第一棵树种在离点M3米远的A处,而且在MA的方向上每隔5米种一棵树 .那么每种一棵树苗时,送树苗所走的路程 S(米)是所种树苗的序号n 的函数.求出它的表达式,并求出它的自变量的取值范围.
分析:植50棵树
即 n≤50
一共要植50棵树
因为从第一棵树开始植,即n≥1
所以自变量的取值范围是: 1≤n≤50,n为整数
所以 1≤n≤50
又因为树苗的序号必须是整数
解:
根据题意得:
S =3+5(n -1)
整理,得函数的表达式 S =5n -2
自变量的取值范围是:1≤n≤50, n 为整数.
小结
(1)初步理解一次函数与正比例函数的概念以及两者之间的关系.
(2)经历了一次函数定义的得出过程,体会了由特殊到一般,再由一般到特殊的研究问题的方法.
小结
(3)
实际问题
↓
一次函数
↓
列函数表达式
判断类型
提取有效信息
审题分析
↓
↓
作业
1. 下列函数中,哪些是一次函数,哪些不是一次函数?在一次函数中,哪些又是正比函数?
(1)
(4)
(2)
(3)
(5)
(6)
作业
2. 一个长方形的一边比另一边长3cm,那么,周长L(cm)是短边长 a(cm)的函数吗?如果是,写出它的表达式,并求出它的自变量的取值范围.想一想,面积 S (cm?)是短边长 a(cm)的一次函数吗?
初二年级 数学
一次函数的概念 (第一课时)
函数
特殊函数
函数的定义
函数的表示方法
函数图象的画法
一般到特殊
{
判断下列每个问题中的两个变量是否构成函数关系.如果是,指出哪一个是自变量,哪一个是因变量,并分别写出每一个函数表达式:
交流
1. 一个长方形的一边长是 3 cm,它的面积
S(cm?)和另一边的长 m(cm)对应.
示意图:
3cm
m
S
分析:(1)在这个问题中存在哪两个变量?
S 和 m
示意图:
3cm
m
S
m ? cm
S ? cm?
3
1
2
3
4
9
6
12
…
…
…
…
分析:(2)它们之间存在函数关系吗?
S 是m 的函数,m 是自变量,S 是因变量.
示意图:
3cm
m
S
分析:(3)你能写出这个函数的表达式吗?
S=3m
(m > 0)
小结:
1.画出示意图,在图上标注已知条件,找到两个变量.
2.通过列表计算分析两个变量之间是否存在函数关系.
3.列函数表达式,确定自变量的取值范围.
2.正方形的面积 S 与它的边长 a 对应.
示意图:
分析:(1)在这个问题中存在哪两个变量?
S 和 a
a
S
示意图:
分析:(2)它们之间存在函数关系吗?
S 是 a 的函数,
a 是自变量,S 是因变量
1
1
2
2
4
3
9
a
S
…
…
…
…
a
S
示意图:
a
S
S = a?
(a > 0)
分析:(3)你能写出这个函数的表达式吗?
3.三角形的面积是 4,它的底边长 a 与这条
边上的高 h 对应.
示意图:
a 和 h
分析:(1)在这个问题中存在哪两个变量?
a
h
面积是4
示意图:
分析:(2)它们之间存在函数关系吗?
a 是 h 的函数,
h 是自变量,a 是因变量.
a
h
面积是4
1
8
2
4
3
4
2
…
…
…
…
a
h
示意图:
a
h
面积是4
分析:(3)你能写出这个函数的表达式吗?
(h>0)
4.等腰三角形顶角的度数 α 和它的一个底角的度数 β 对应.
示意图:
分析:(1)在这个问题中存在哪两个变量?
α 和 β
示意图:
分析:(2)它们之间存在函数关系吗?
α 是 β 的函数,
β 是自变量,α 是因变量.
示意图:
分析:(3)你能写出这个函数的表达式吗?
α+2β =180
α =180 -2β
思考:你能求出自变量的取值范围吗?
分析:
α =180 -2β
180 -2β > 0
β < 90
所以自变量的取值范围是 0<β<90
β >0
α >0
{
β >0
{
β<90
示意图:
函数表达式: α =180 -2β
(0<β<90)
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
分析:最大量程为 5 N
即 p≤5
弹簧秤所能承受的最大物重为5 N
又因为 p≥0
所以 0≤p≤5
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
分析:原长度是15cm
即弹簧秤未挂重物时,它的自然长度是15 cm.
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
…
0.5
0.5+15
0.5×2
0.5×2+15
0.5×3
0.5×3+15
0.5×4
0.5×4+15
1
2
3
4
…
…
p
0.5p
物重
(p ? N )
伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
伸长长度
(cm)
总长度
(L ? cm)
5.某种最大量程为5 N的弹簧测力计,弹簧的原长度是 15 cm, 挂物每增加 1 N 时,弹簧伸长 0. 5 cm,这时,伸长后弹簧的总长度 L(cm)和所称物重 p(N)对应 .
伸长后弹簧的总长度 L(cm)是所称物重 p(N)的函数,其中 p 是自变量,L 是因变量.
…
0.5
0.5+15
0.5×2
0.5×2+15
0.5×3
0.5×3+15
0.5×4
0.5×4+15
1
2
3
4
…
…
p
0.5p
物重
(p ? N )
伸长长度
(cm)
总长度
(L ? cm)
你能写出这个函数的表达式吗?
…
0.5
0.5×1+15
0.5×2
0.5×2+15
0.5×3
0.5×3+15
0.5×4
0.5×4+15
1
2
3
4
…
…
p
0.5p
物重
(p ? N )
伸长长度
(cm)
总长度
(L ? cm)
你能写出这个函数的表达式吗?
0.5p+15
你能写出这个函数的表达式吗?
L =0.5p+15
思考:你能求出自变量的取值范围吗?
或L =15+0.5p
分析:最大量程为 5 N
即 p≤5
弹簧秤所能承受的最大物重为5 N
又因为 p≥0
所以0≤p≤5
函数的表达式:
(0≤p≤5)
L =0.5p+15
(1)S = 3m (2)S = a?
(3) (4)α =180 -2β
(5)L=0.5p+15
函数表达式:
3m ,a? , ,180 -2β ,0.5p+15
思考:你能将它们分类吗?分类的标准是什么?
a =
3m ,180 -2β , ,a? ,0.5p+15
关注
自变量的次数
自变量的系数
自变量的位置
有无常数项
3m ,180 -2β , ,a? ,0.5p+15
按自变量的
次数分类
二次
S =a?
一次
α =180-2β
S =3m
L =0.5p+15
{
负一次
a =
思考:等号右边含有自变量的代数式有什么共同的特征?
自变量的次数是1次
S =3m
a =180-2β
L =0.5p+15
一次函数
S =3m
a =180-2β
L =0.5p+15
思考:等号右边含有自变量的代数式的结构有什
么共同的特征?
右边:自变量与常数的积再加上常数项
a =-2β+180
加法交换律
S =3m
a =180-2β
L =0.5p+15
S =3m+0
右边:自变量与常数的积再加上常数项
S =3m
a =180-2β
L =0.5p+15
思考:你能用一个一般的函数表达式来概括这三
个表达式的结构特征吗?
y =kx +b(k,b为常数)
右边:自变量与常数的积再加上常数项
k
b
函数表达式:y = kx +b(k,b为常数)
思考:对于常数k的取值有限制吗?它可以为0吗?
所以k≠0,即自变量的系数不能为0
k =0时,
y =b ,
自变量的次数不是1次
函数表达式:y = kx +b(k,b为常数,且k≠0)
思考:对于常数k的取值有限制吗?它可以为0吗?
所以k≠0,即自变量的系数不能为0
k =0时,
y =b ,
自变量的次数不是1次
函数表达式:y = kx +b(k,b为常数,且k≠0)
思考:常数 b 的取值可以为0吗?
b= 0时, y = kx
(k为常数, k≠0)
正比例函数
一次函数:
一般地,我们把形如y =kx +b(k,b为常数,且k≠0)的函数叫做一次函数.其中 x 是自变量.
正比例函数:
当b=0时,一次函数y=kx(k≠0)又叫做正比
例函数.
思考:
一次函数y =kx +b(k,b是常数,且k≠0)自变量的取值范围是什么呢?
自变量的取值范围:全体实数
你能说说一次函数与正比例函数的关系吗?
一次函数包含正比例函数,
正比例函数是特殊的一次函数.
你能用一个图来表示它们之间的关系吗?
一次函数
正比例函数
例1 判断下列函数中,哪些是一次函数,一次函
数中哪些是正比例函数?
(5)
(1)
(2)
(3)
(4)
(6)
分析:
要想判断一个函数是否为一次函数,根据定义,只需判断函数表达式是否可以写成 y=kx +b(k,b为常数,且k≠0)的形式,即是否满足两个条件:(1)自变量的次数为1次,(2)自变量的系数不为0.
例1 判断下列函数中,哪些是一次函数,一次函
数中哪些是正比例函数?
(5)
(1)
(2)
(3)
(4)
(6)
例1 判断下列函数中,哪些是一次函数,一次函
数中哪些是正比例函数?
解:一次函数:
(1)
(2)
(4)
(6)
正比例函数:
(6)
(1)若它是一次函数,求 k 的值.
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(2)若它是正比例函数,求 k 的值.
分析:
{
自变量的次数为一次
k -2≠0
∴
k≠2
(1)若它是一次函数,求 k 的值.
自变量的系数不等于0
∴
自变量的系数
常数项
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(1)若它是一次函数,求 k 的值.
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
解:由题意得
k -2≠0
k≠2
∴
(2)若它是正比例函数,求 k 的值.
分析:
自变量的次数为一次
自变量的系数不等于0
常数项为0
{
自变量的系数
常数项
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(2)若它是正比例函数,求 k 的值.
k +1 0
k - 2 0
∴
k = -1
把k = -1代入k -2中,k - 2≠0成立
∴
分析:
k = -1
{
自变量的系数
常数项
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
(2)若它是正比例函数,求 k 的值.
例2 已知函数 y=(k -2)x +k +1,其中k为常数.
.
{
k +1= 0
k-2≠0
∴
k = -1
把k = -1代入k -2中,k - 2≠0成立
∴
k = -1
解:由题意得
例3 八年级一班学生接受了在公路的一边植50棵树的任务.树苗堆放在公路边的M处.现规定,第一棵树种在离点M3米远的A处,而且在MA的方向上每隔5米种一棵树 .那么每种一棵树苗时,送树苗所走的路程 S(米)是所种树苗的序号n 的函数.求出它的表达式,并求出它的自变量的取值范围.
分析:
50棵树
M
A
MA=3米
①
②
③
B
C
AB=BC=5米
分析:
50棵树
M
A
MA=3米
①
②
③
B
C
AB=BC=5米
n/棵
S/米
1
3
2
…
…
n
3
3+5×1
3+5×2
4
3+5×3
↓
3+5×0
S = 3+5(n -1)
自变量的取值范围是什么呢?
→
S =5n -2
n/棵
S/米
1
3
2
…
…
n
3
3+5×1
3+5×2
4
3+5×3
3+5(n -1)
例3 八年级一班学生接受了在公路的一边植50棵树的任务.树苗堆放在公路边的M处.现规定,第一棵树种在离点M3米远的A处,而且在MA的方向上每隔5米种一棵树 .那么每种一棵树苗时,送树苗所走的路程 S(米)是所种树苗的序号n 的函数.求出它的表达式,并求出它的自变量的取值范围.
分析:植50棵树
即 n≤50
一共要植50棵树
因为从第一棵树开始植,即n≥1
所以自变量的取值范围是: 1≤n≤50,n为整数
所以 1≤n≤50
又因为树苗的序号必须是整数
解:
根据题意得:
S =3+5(n -1)
整理,得函数的表达式 S =5n -2
自变量的取值范围是:1≤n≤50, n 为整数.
小结
(1)初步理解一次函数与正比例函数的概念以及两者之间的关系.
(2)经历了一次函数定义的得出过程,体会了由特殊到一般,再由一般到特殊的研究问题的方法.
小结
(3)
实际问题
↓
一次函数
↓
列函数表达式
判断类型
提取有效信息
审题分析
↓
↓
作业
1. 下列函数中,哪些是一次函数,哪些不是一次函数?在一次函数中,哪些又是正比函数?
(1)
(4)
(2)
(3)
(5)
(6)
作业
2. 一个长方形的一边比另一边长3cm,那么,周长L(cm)是短边长 a(cm)的函数吗?如果是,写出它的表达式,并求出它的自变量的取值范围.想一想,面积 S (cm?)是短边长 a(cm)的一次函数吗?
同课章节目录
