北师大版数学七年级下册1.5平方差公式(第2课时)说课教案
文档属性
| 名称 | 北师大版数学七年级下册1.5平方差公式(第2课时)说课教案 |  | |
| 格式 | zip | ||
| 文件大小 | 51.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 15:36:38 | ||
图片预览

文档简介
5 平方差公式(第2课时)
1、 学生起点分析
学生通过上一节课的学习,已经经历了探索和推导平方差公式的过程,并能运用公式进行简单的计算,同时前面有理数运算、整式运算等基础知识以及基本技能的学习,为本节课的学习奠定了知识技能基础.
2、 教学目标
1.知识与技能:经历探索平方差公式的过程,会通过图形的拼接验证平方差公式,了解平方差公式的几何背景,并会运用所学的知识,进行简单的混合运算.
2.过程与方法:通过创设问题情境,让学生在数学活动中建立平方差公式模型,通过探索规律,归纳出利用平方差公式,解决数字运算问题的方法,培养学生观察、归纳、应用能力.
3.情感与态度: 了解平方差公式的几何背景,培养学生的数形结合意识.在探究学习中体会数学的现实意义,培养学习数学的信心.
三、教学过程设计
基于对教材以及教学任务的分析,本节课设计了五个教学环节:复习旧知、引入新课;创设情境、探究结论;观察思考、拓展延伸;典例分析、巩固提高;当堂达标、自我检测;课堂小结、布置作业.
第一环节 复习旧知、引入新课
活动内容:回顾上节课平方差公式
平方差公式:(a+b)(a-b)=a2-b2
1.公式的结构特点:左边是两个二项式的乘积,即两数和与这两数差的积;
右边是两数的平方差.
2.应用平方差公式的注意事项:
1)注意平方差公式的适用范围
2)字母a、b可以是数,也可以是整式
3)注意计算过程中的符号和括号
第二环节 创设情境、探究结论
活动内容:
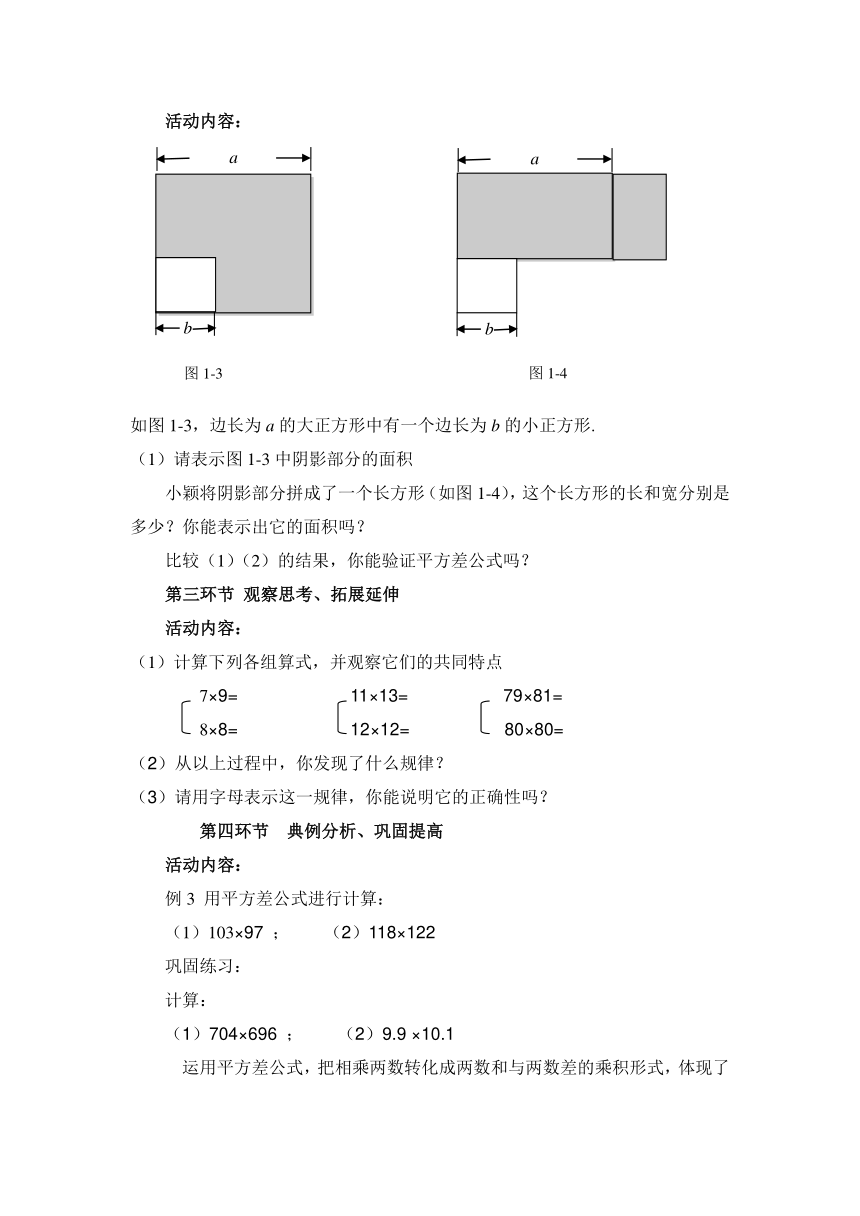
如图1-3,边长为a的大正方形中有一个边长为b的小正方形.
(1)请表示图1-3中阴影部分的面积
小颖将阴影部分拼成了一个长方形(如图1-4),这个长方形的长和宽分别是多少?你能表示出它的面积吗?
比较(1)(2)的结果,你能验证平方差公式吗?
第三环节 观察思考、拓展延伸
活动内容:
(1)计算下列各组算式,并观察它们的共同特点
7×9= 11×13= 79×81=
8×8= 12×12= 80×80=
(2)从以上过程中,你发现了什么规律?
(3)请用字母表示这一规律,你能说明它的正确性吗?
第四环节 典例分析、巩固提高
活动内容:
例3 用平方差公式进行计算:
(1)103×97 ; (2)118×122
巩固练习:
计算:
(1)704×696 ; (2)9.9 ×10.1
运用平方差公式,把相乘两数转化成两数和与两数差的乘积形式,体现了转化的思想和数式通性,让学生体会到,利用公式可以进行一些有关于数的简便运算,目的是进一步巩固平方差公式,体会符号运算对于解决问题的作用.
活动内容:
例4 计算:
(1)a2(a+b)(a-b)+a2b2 ; (2)(2x-5)(2x+5)-2x(2x-3)
巩固练习:
计算:
(1)(x+2y)(x-2y)+(x+1)(x-1); (2)x(x-1)-
设计必要练习,使学生准确的运用平方差公式,进行简单的混合运算,并能明白每一步计算的算理,提高综合运用公式的能力.
第五环节 当堂达标、自我检测
活动内容: 计算:
(1) 2001×1999 -20002
(2) (3mn+1)(3mn-1)-8m2n2
(3) -(x+8)
为学生提供自我检测的机会,及时反馈,查漏补缺.
第六环节 课堂小结、布置作业
活动内容:
1.平方差公式:
1)公示的符号表示:(a+b)(a-b)=a2-b2 ;
2)公式的结构特点:左边是两个二项式的乘积,即两数和与这两数差的积;右边是两数的平方差.
3)公式的几何解释:
2.应用平方差公式的注意事项:
1)注意平方差公式的适用范围
2)字母a、b可以是数,也可以是整式
3)注意计算过程中的符号和括号
通过课堂小结对课堂知识点的回顾,让学生分享自己在学习过程中遇到的挫折以及积累的经验,构建自己的知识体系,同时提出自己存在的困惑,大家一起解决,从而达到巩固所学知识的目的.
布置作业
1. 必做题:教材习题1.10
2. 选做题:计算:(21+1)(22+1)(24+1)(28+1)(216+1)(232+1)(264+1)
4、 教学设计反思
教学中,教师应该有意识地培养学生的推理能力,鼓励学生通过合情推理进行大胆猜测,然后利用符号间的运算验证猜测或解决问题,同时鼓励学生有条理的表达自己的思考过程.同时注意评价方式多元化,使每个学生都能在数学学习中,收获成功体验,从而培养学习数学的兴趣和信心.
a
b
a
b
图1-3
图1-4
a
b
a
b
图1-4
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
