四年级下册数学课件9.5 鸡兔同笼苏教版 (共16张PPT)
文档属性
| 名称 | 四年级下册数学课件9.5 鸡兔同笼苏教版 (共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-13 20:55:27 | ||
图片预览





文档简介
(共16张PPT)
鸡兔同笼
学习目标:
一、了解“鸡兔同笼”的历史及趣味性;
二、完成小研究中解决问题的方法:
1、列表法。(它的优点及缺陷)
2、假设法。
3、总结出“鸡兔同笼”的公式。
4、解决实际问题。
三、以小组为单位,能否自己再找一找其他方法。
了解鸡兔同笼历史:鸡兔同笼是中国古代的数学名题之一,大约在1500年前《孙子算经》中就记载了这个有趣的问题。中是这样叙述的:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数有94只脚。问笼中各有多少只鸡和兔?
笼子里有若干只鸡和兔,从上面数有8个头,从下面数有26条腿,鸡、兔各有几只?
想一想
我们可以先从简单问题的入手。
试试列表法
返回
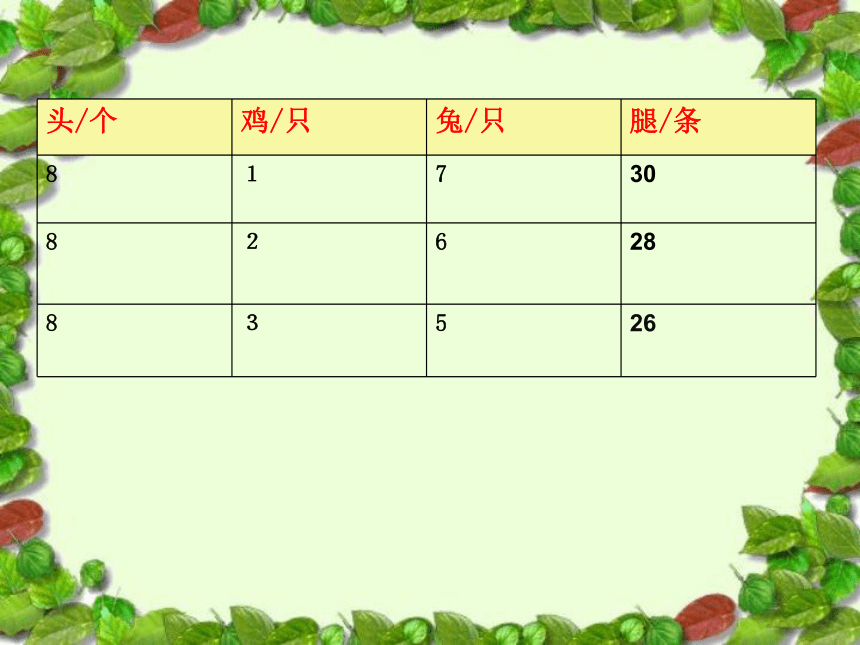
头/个 鸡/只 兔/只 腿/条
8 1 7 30
8 2 6 28
8 3 5 26
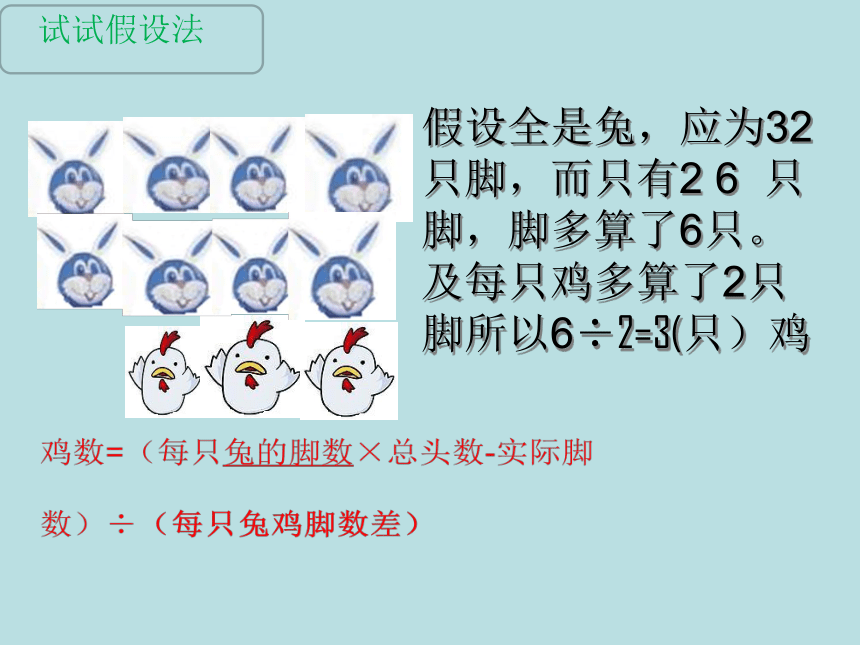
假设全是兔,应为32只脚,而只有2 6 只脚,脚多算了6只。及每只鸡多算了2只脚所以6÷2=3(只)鸡
试试假设法
一队强盗一队狗,二队拼作一队走,数头一共三百六,
数腿一共八百九,问有多少强盗多少狗?
假设全是强盗:360x2=720(个)
890-720=170(个)
狗:170÷2=85(只)
强盗:360-85=275(个)
小明的储蓄罐里有1角和5角硬币共7枚,价值1.9元,1角和5角的硬币各有多少枚?
生活中的数学
假设全是一角:1.9元是19枚1角硬币,
但是只有7枚,多了:19-7=12(枚)
5-1=4(角)
5角硬币:12÷4=3(枚)
有角硬币:7-3=4(枚)
生活中的数学
生活中的数学
假设全做对,得分:20x5=100(分)
实际得分52分,少了:100-52=48(分)
错一题倒扣3分,实际少得分5+3=8(分)
所以错题:48÷8=6(道)
全对题数:20-6=14(道)
你还有哪些方法?
试一试:抬腿法:
方法一
假如让鸡抬起一只脚,兔子抬起2只脚,
这时笼子还有26÷2=13(只)脚。
笼子里的兔就比鸡的脚数多1,这时,脚
与头的总数之差13-8=5(只),
就是兔子的只数。
方法二:
假如鸡与兔子都抬起两只脚,
还剩下26-8×2=10(只)脚 ,
这时鸡是屁股坐地上,地上只有兔子的脚
而且每只兔子有两只脚在地上,所以有
10÷2=5(只)兔子,就有8-5=3(只)鸡。
方法三:
我们可以先让兔子抬起2只脚,那么现在就有
8×2=16(只)脚,脚数和原来差26-16=10(只)
差的是每只兔子抬起的2只脚,一共抬起了10只脚
所以用10÷2=5(只)兔子,8-5=3(只)鸡。
这节课你有什么收获......
鸡兔同笼
学习目标:
一、了解“鸡兔同笼”的历史及趣味性;
二、完成小研究中解决问题的方法:
1、列表法。(它的优点及缺陷)
2、假设法。
3、总结出“鸡兔同笼”的公式。
4、解决实际问题。
三、以小组为单位,能否自己再找一找其他方法。
了解鸡兔同笼历史:鸡兔同笼是中国古代的数学名题之一,大约在1500年前《孙子算经》中就记载了这个有趣的问题。中是这样叙述的:今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?这四句话的意思是:有若干只鸡兔同在一个笼子里,从上面数,有35个头,从下面数有94只脚。问笼中各有多少只鸡和兔?
笼子里有若干只鸡和兔,从上面数有8个头,从下面数有26条腿,鸡、兔各有几只?
想一想
我们可以先从简单问题的入手。
试试列表法
返回
头/个 鸡/只 兔/只 腿/条
8 1 7 30
8 2 6 28
8 3 5 26
假设全是兔,应为32只脚,而只有2 6 只脚,脚多算了6只。及每只鸡多算了2只脚所以6÷2=3(只)鸡
试试假设法
一队强盗一队狗,二队拼作一队走,数头一共三百六,
数腿一共八百九,问有多少强盗多少狗?
假设全是强盗:360x2=720(个)
890-720=170(个)
狗:170÷2=85(只)
强盗:360-85=275(个)
小明的储蓄罐里有1角和5角硬币共7枚,价值1.9元,1角和5角的硬币各有多少枚?
生活中的数学
假设全是一角:1.9元是19枚1角硬币,
但是只有7枚,多了:19-7=12(枚)
5-1=4(角)
5角硬币:12÷4=3(枚)
有角硬币:7-3=4(枚)
生活中的数学
生活中的数学
假设全做对,得分:20x5=100(分)
实际得分52分,少了:100-52=48(分)
错一题倒扣3分,实际少得分5+3=8(分)
所以错题:48÷8=6(道)
全对题数:20-6=14(道)
你还有哪些方法?
试一试:抬腿法:
方法一
假如让鸡抬起一只脚,兔子抬起2只脚,
这时笼子还有26÷2=13(只)脚。
笼子里的兔就比鸡的脚数多1,这时,脚
与头的总数之差13-8=5(只),
就是兔子的只数。
方法二:
假如鸡与兔子都抬起两只脚,
还剩下26-8×2=10(只)脚 ,
这时鸡是屁股坐地上,地上只有兔子的脚
而且每只兔子有两只脚在地上,所以有
10÷2=5(只)兔子,就有8-5=3(只)鸡。
方法三:
我们可以先让兔子抬起2只脚,那么现在就有
8×2=16(只)脚,脚数和原来差26-16=10(只)
差的是每只兔子抬起的2只脚,一共抬起了10只脚
所以用10÷2=5(只)兔子,8-5=3(只)鸡。
这节课你有什么收获......
