人教版七年级下册易错题专项训练5.4平移(含解析)
文档属性
| 名称 | 人教版七年级下册易错题专项训练5.4平移(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-16 17:58:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版七年级下册易错题专题
5.4 平移
一.选择题(共1小题)
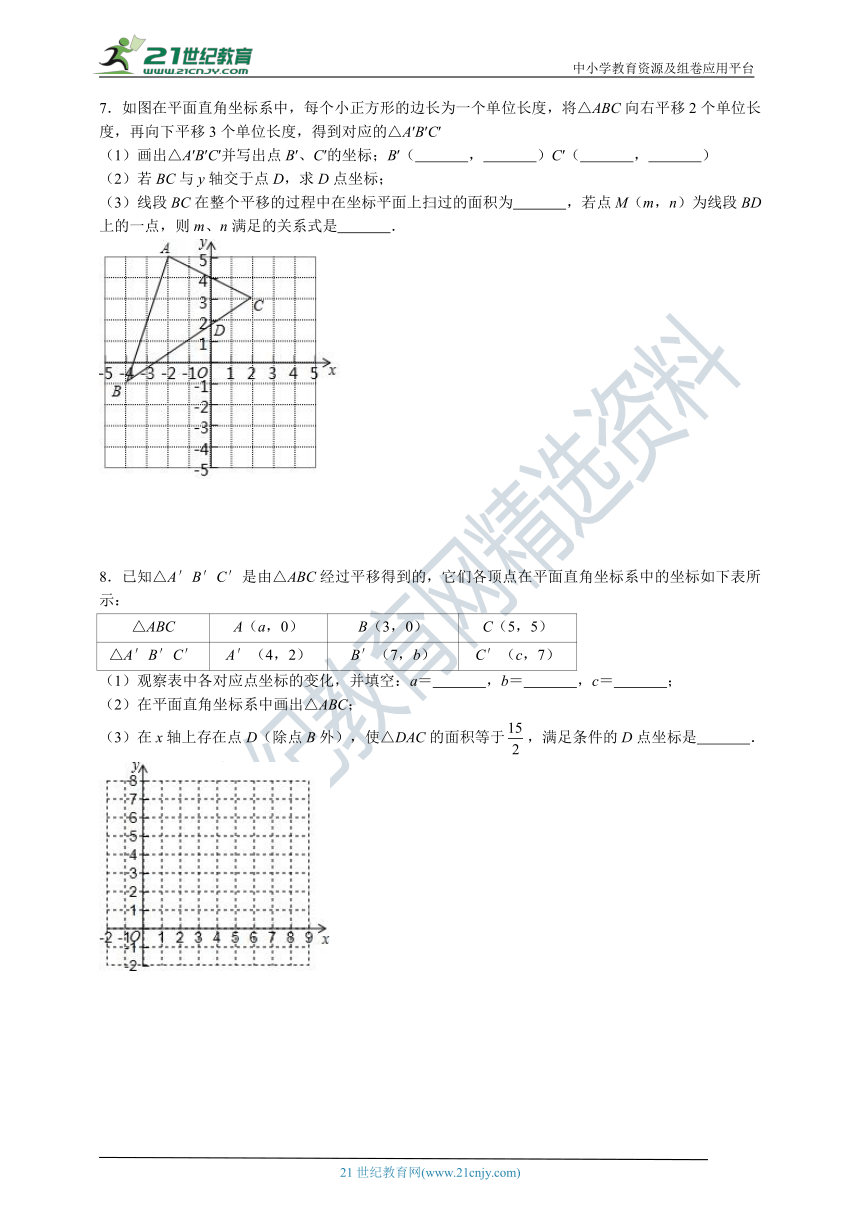
1.如图,把△ABC沿着BC的方向平移到△DEF的位置,它们重叠部分的面积是△ABC面积的一半,若BC=4,则△ABC移动的距离是( )
A.2 B.2 C.1 D.4-2
二.填空题(共1小题)
2.在如图所示的正方形网格中,每个小正方形的边长为1各单位,格点三角形(顶点是网格线的交点的三角形)△ABC的顶点A,B的坐标分别为(1,4),(-3,1).
(1)请在网格所在的平面内作出符合上述表述的平面直角坐标系;
(2)请你将A、B、C的横坐标不变,纵坐标乘以-1所得到的点A1、B1、C1描在坐标系中,并画出△A1B1C1,其中点C1的坐标为 .
(3)△ABC的面积是 .
三.解答题(共7小题)
3.如图,直线CB∥OA,∠C=∠A=112°,E,F在CB上,且满足∠FOB=∠AOB,DE平分∠COF.
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.
4.如图,已知直线l1∥l2,点A、B在直线l1上,点C、D在直线l2上,点C在点D的右侧,∠ADC=80°,∠ABC=n°,BE平分∠ABC,DE平分∠ADC,直线BE、DE交于点E.
(1)写出∠EDC的度数 ;
(2)试求∠BED的度数(用含n的代数式表示);
(3)将线段BC向右平行移动,其他条件不变,请直接写出∠BED的度数(用含n的代数式表示)
5.已知:BC∥OA,∠B=∠A=120°,试回答下列问题:
(1)如图1所示,求证:OB∥AC;
(2)如图2,若点E、F在BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF,则∠EOC的度数是 ;
(3)在(2)的条件下,若平行移动AC,其它条件不变,如图3,则∠OCB:∠OFB的值是 .
6.在一次数学课上,张老师让同学们独立完成课本第23页7.选择题(2)
如图1,如果AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=
A.180° B.270° C.360° D.540°
(1)请你也完成这道题;
(2)在同学们都正确解答这道题后,张老师对这道题进行了变式:
在(1)中AB∥EF不变,将点C移动到点C1位置(如图2所示),写出∠BAC1,∠AC1E,∠C1EF之间的数量关系,并证明.
请你和这个班的同学一起解答这道题吧;
(3)善于思考的小明想:将图1平移至与图2重合(如图3所示),当AC1,EC1分别平分∠BAC,∠CEF时,那么∠ACE与∠AC1E之间有怎样的数量关系?请你直接写出结果,不需要证明.
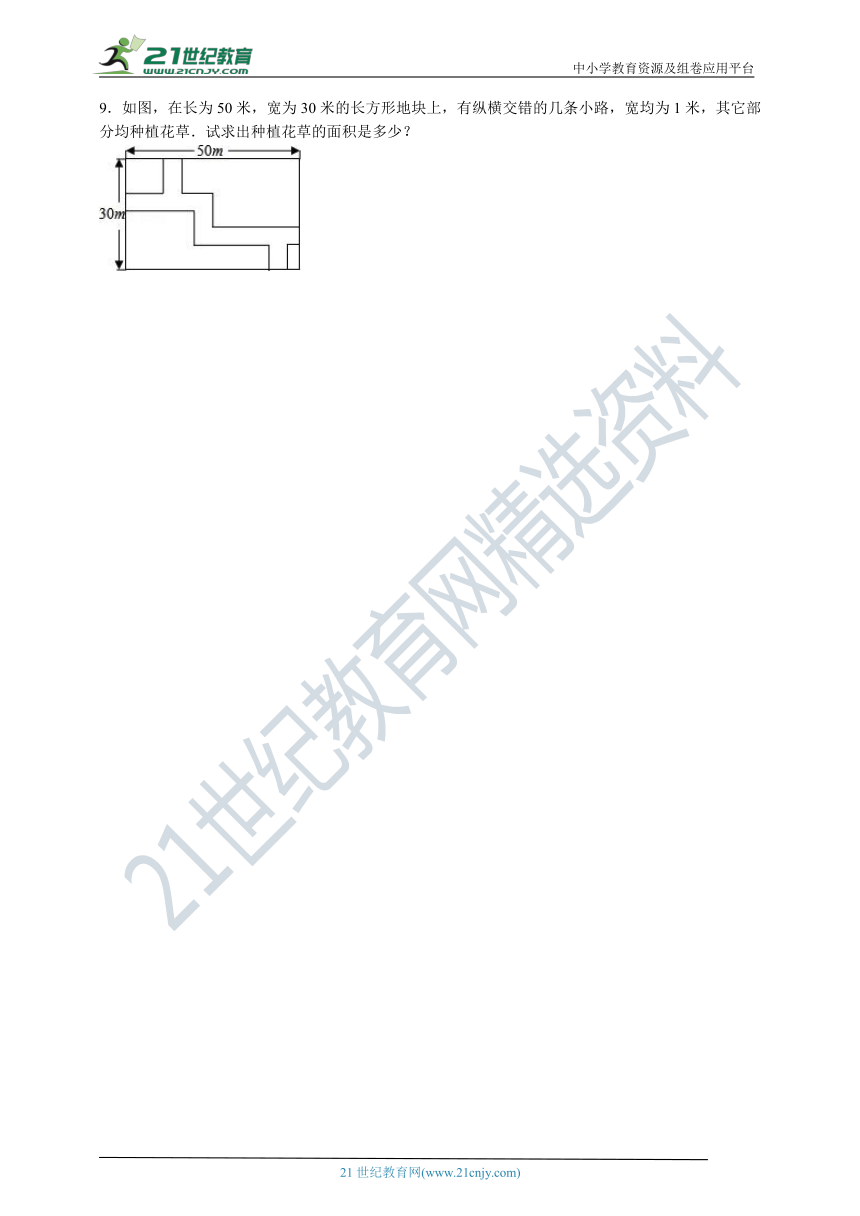
7.如图在平面直角坐标系中,每个小正方形的边长为一个单位长度,将△ABC向右平移2个单位长度,再向下平移3个单位长度,得到对应的△A′B′C′
(1)画出△A′B′C′并写出点B′、C′的坐标;B′( , )C′( , )
(2)若BC与y轴交于点D,求D点坐标;
(3)线段BC在整个平移的过程中在坐标平面上扫过的面积为 ,若点M(m,n)为线段BD上的一点,则m、n满足的关系式是 .
8.已知△A′B′C′是由△ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
△ABC A(a,0) B(3,0) C(5,5)
△A′B′C′ A′(4,2) B′(7,b) C′(c,7)
(1)观察表中各对应点坐标的变化,并填空:a= ,b= ,c= ;
(2)在平面直角坐标系中画出△ABC;
(3)在x轴上存在点D(除点B外),使△DAC的面积等于,满足条件的D点坐标是 .
9.如图,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草.试求出种植花草的面积是多少?
参考答案
一.选择题
1.解:∵△ABC沿BC边平移到△DEF的位置,
∴AB∥DE,
∴△ABC∽△HEC,
∴=()2=,
∴EC:BC=1:,
∵BC=4,
∴EC=2,
∴BE=BC-EC=4-2.
故选:D.
二.填空题
2.解:(1)平面直角坐标系如图所示;
(2)如图所示,△A1B1C1即为所求,其中点C1的坐标为(5,2);
故答案为:(5,2);
(3)△ABC的面积是×6×(3+3)=18.
故答案为:18.
三.解答题
3.解:(1)∵CB∥OA,
∴∠AOC=180°-∠C=180°-112°=68°,
∵OE平分∠COF,
∴∠COE=∠EOF,
∵∠FOB=∠AOB,
∴∠EOB=∠EOF+∠FOB=∠AOC=×68°=34°;
(2)∠OBC:∠OFC的值不变.
∵CB∥OA,
∴∠AOB=∠OBC,
∵∠FOB=∠AOB,
∴∠FOB=∠OBC,
∴∠OFC=∠FOB+∠OBC=2∠OBC,
∴∠OBC:∠OFC=1:2,是定值;
(3)在△COE和△AOB中,
∵∠OEC=∠OBA,∠C=∠OAB,
∴∠COE=∠AOB,
∴OB、OE、OF是∠AOC的四等分线,
∴∠COE=∠AOC=×68°=17°,
∴∠OEC=180°-∠C-∠COE=180°-112°-17°=51°,
故存在某种情况,使∠OEC=∠OBA,此时∠OEC=∠OBA=51°.
4.解:(1)∵DE平分∠ADC,∠ADC=80°,
∴∠EDC=∠ADC=×80°=40°,
故答案为:40°;
(2)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠CDE=∠DEF,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=40°,
∴∠BED=∠BEF+∠DEF=n°+40°;
(3)过点E作EF∥AB,
①如图1,点A在点B的右边时,同(2)可得,∠BED不变,为n°+40°;
②如图2,点A在点B的左边时,
∵BE平分∠ABC,DE平分∠ADC,∠ABC=n°,∠ADC=80°,
∴∠ABE=∠ABC=n°,∠CDE=∠ADC=40°,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠BEF=180°-∠ABE=180°-n°,∠CDE=∠DEF=40°,
∴∠BED=∠BEF+∠DEF=180°-n°+40°=220°-n°,
综上所述,∠BED的度数变化,度数为n°+40°或220°-n°.
5.解:(1)∵BC∥OA,
∴∠A+∠C=180°,
又∵∠B=∠A,
∴∠B+∠C=180°,
∴OB∥AC;
(2)∵BC∥OA,∠B=∠A=120°,
∴∠AOB=60°,
∵∠FOC=∠AOC,且OE平分∠BOF,
∴∠EOF=BOF,∠COF=∠AOF,
∴∠EOC=∠AOB=30°,
故答案为:30°;
(3)∵BC∥OA,
∴∠OCB=∠AOC,∠OFB=∠AOF,
∵∠FOC=∠AOC,
∴∠AOC:∠AOF=1:2,
∴∠OCB:∠OFB=1:2.
故答案为:1:2.
6.解:(1)∵AB∥CD∥EF,
∴∠A+∠ACD=180°,∠E+∠ECD=180°,
∴∠A+∠ACD+∠E+∠ECD=360°,
即∠BAC+∠ACE+∠CEF=360°,
故选:C.
(2)∠BAC1+∠C1EF=∠AC1E,
如图,过C1作C1G∥AB,
∵AB∥EF,
∴C1G∥AB∥EF,
∴∠A=∠AC1G,∠E=∠EC1G,
∴∠A+∠E=∠AC1G+∠EC1G=∠AC1E;
(3)∠C+∠2∠AC1E=360°,
理由:由(1)可得,∠BAC+∠C+∠CEF=360°,
由(2)可得,∠C1=∠BAC1+∠C1EF,
又∵AC1,EC1分别平分∠BAC,∠CEF,
∴∠BAC=2∠BAC1,∠CEF=2∠C1EF,
∴2∠BAC1+∠C+2∠C1EF=360°,
即2(∠BAC1+∠C1EF)+∠C=360°,
∴∠C+2∠AC1E=360°.
7.解:(1)如图所示,△A′B′C′即为所求,B′(-2,-4),C′(4,0);
(2)由图象知,B(-4,-1),C(2,3),
设直线BC的解析式为y=kx+b,
∴,解得,
∴直线BC的解析式为y=x+,
当x=0时,y=,
∴D(0,).
(3)线段BC在整个平移的过程中在坐标平面上扫过的面积为:2×4+3×6=26;
把M(m,n)代入y=x+,可得n=m+.
故答案为:26,n=m+.
8.解:(1)由表格得出对应点为:A(a,0),A′(4,2);B(3,0),B′(7,b);C(5,5),C′(c,7),
∴平移后的点的横坐标加4,纵坐标加2,
∴a=0,b=2,c=9.
故答案为:0,2,9;
(2)如图所示,△ABC即为所求;
(3)∵△DAC的面积等于,
∴AD×5=,
∴AD=3,
又∵A(0,0),B(3,0),
∴D点坐标是(-3,0).
故答案为:(-3,0).
9.解:根据题意,小路的面积相当于横向与纵向的两条小路,
种植花草的面积=(50-1)(30-1)=1421m2.
故答案为:1421m2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
