北师大版数学七年级下册4.5利用三角形全等测距离同步练习(含答案)
文档属性
| 名称 | 北师大版数学七年级下册4.5利用三角形全等测距离同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 167.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 16:27:30 | ||
图片预览

文档简介
4.5利用三角形全等测距离
一、选择题
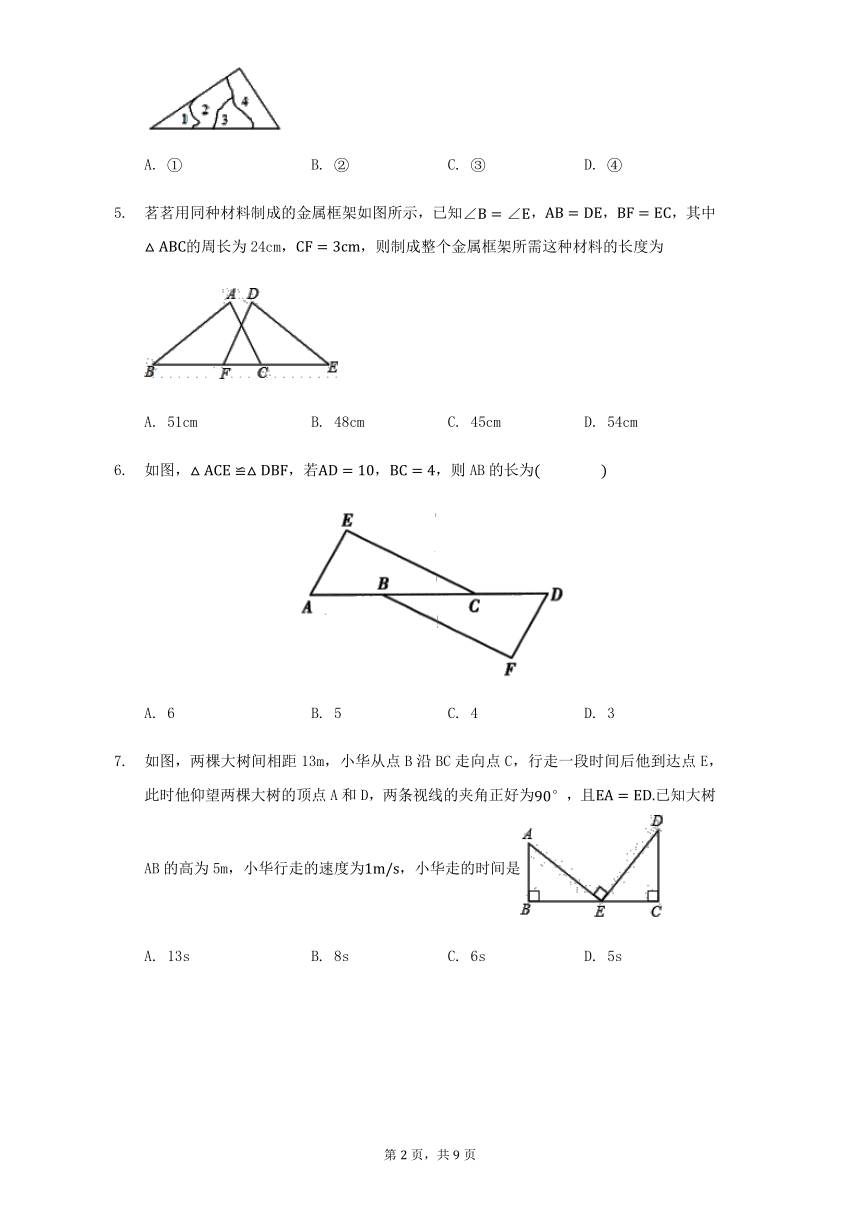
如图所示,A、B在一水池两侧,若,,,则水池宽AB为
A. 8m B. 10m C. 12m D. 无法确定
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的
A. SSS B. ASA C. AAS D. SAS
如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作,可得≌,所以,所以测量的长即可得AB的长,判定图中两个三角形全等的理由是
A. SAS B. ASA C. SSS D. AAS
如图所示,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带去.
A. B. C. D.
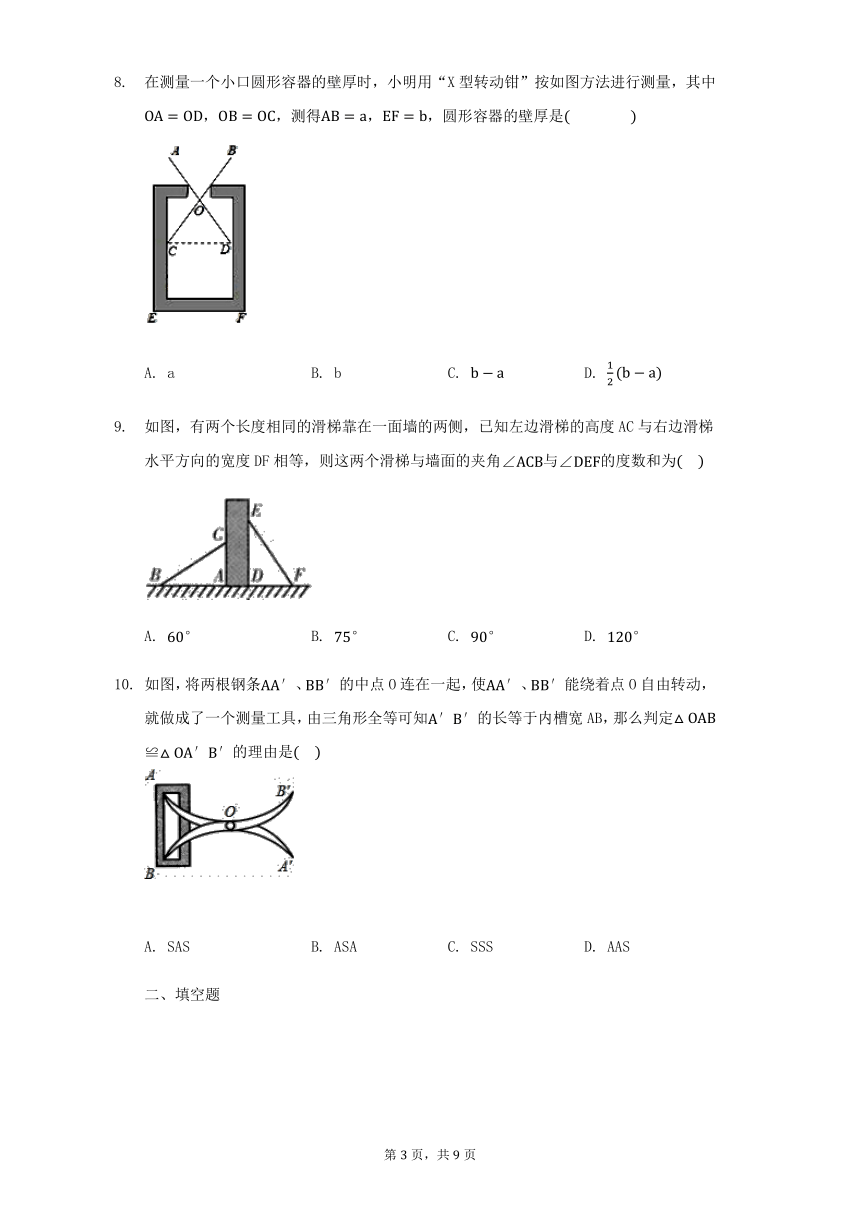
茗茗用同种材料制成的金属框架如图所示,已知,,,其中的周长为24cm,,则制成整个金属框架所需这种材料的长度为
A. 51cm B. 48cm C. 45cm D. 54cm
如图,,若,,则AB的长为? ? ?
A. 6 B. 5 C. 4 D. 3
如图,两棵大树间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为,且已知大树AB的高为5m,小华行走的速度为,小华走的时间是
A. 13s B. 8s C. 6s D. 5s
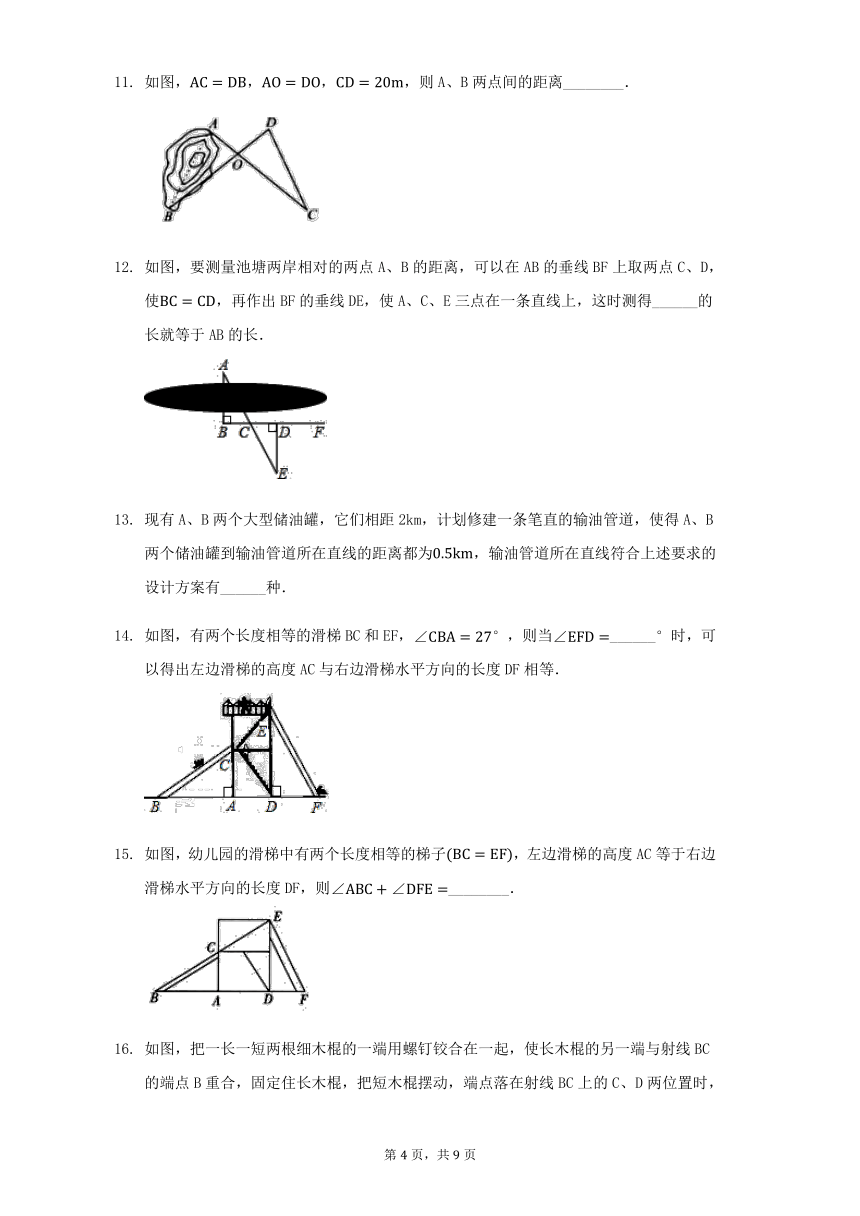
在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中,,测得,,圆形容器的壁厚是? ? ?
A. a B. b C. D.
如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角与的度数和为
A. B. C. D.
如图,将两根钢条、的中点O连在一起,使、能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知的长等于内槽宽AB,那么判定≌的理由是
A. SAS B. ASA C. SSS D. AAS
二、填空题
如图,,,,则A、B两点间的距离________.
如图,要测量池塘两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使,再作出BF的垂线DE,使A、C、E三点在一条直线上,这时测得______的长就等于AB的长.
现有A、B两个大型储油罐,它们相距2km,计划修建一条笔直的输油管道,使得A、B两个储油罐到输油管道所在直线的距离都为,输油管道所在直线符合上述要求的设计方案有______种.
如图,有两个长度相等的滑梯BC和EF,,则当______时,可以得出左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.
如图,幼儿园的滑梯中有两个长度相等的梯子,左边滑梯的高度AC等于右边滑梯水平方向的长度DF,则________.
如图,把一长一短两根细木棍的一端用螺钉铰合在一起,使长木棍的另一端与射线BC的端点B重合,固定住长木棍,把短木棍摆动,端点落在射线BC上的C、D两位置时,形成和此时,,,但是和不全等,这说明______.
如图,是小明荡秋千的侧面示意图,秋千链长秋千踏板视作一个点,静止时秋千位于铅垂线BC上,此时秋千踏板到地面的距离为当秋千踏板摆动到点D时,点D到BC的距离若他从D处摆动到处时,恰好,则到地面的距离为__________m.
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中,,晓明同学在探究筝形的性质时,得到如下结论:≌;;;其中,正确的结论有______个.
如图,在中,,点M在线段AB上,,,垂足为G,MG与BC交于点若,则________cm.
课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间如图,,,每块砌墙用的砖块厚度为8cm,小聪很快就知道了两个墙脚之间的距离DE的长为______cm.
三、解答题
小强为了测量一幢高楼AB的高度,在旗杆CD与楼之间选定一点测得旗杆顶C视线PC与地面夹角,测得楼顶A视线PA与地面夹角,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为米,小强计算出了楼高,楼高AB是多少米?
某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
在河流的一条岸边B点,选对岸正对的一棵树A;
沿河岸直走20m有一树C,继续前行20m到达D处;
从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
测得DE的长为5米.
求:河的宽度是多少米?
请你证明他们做法的正确性.
【答案】
1. B 2. D 3. B 4. D 5. C 6. D 7. B
8. D 9. C 10. A
11. 20m??
12. DE??
13. 4??
14. 63??
15. ??
16. 两边及一边对角对应相等的两个三角形不一定全等??
17. ??
18. 3??
19. 4??
20. 56??
21. 解:,,,
.
在和中,
≌.
.
米,米,
米.
答:楼高AB是26米.??
22. 解:河的宽度是5m;
证明:由作法知,,,
在和中,
,
≌,
,
即他们的做法是正确的.??
第2页,共2页
第1页,共1页
一、选择题
如图所示,A、B在一水池两侧,若,,,则水池宽AB为
A. 8m B. 10m C. 12m D. 无法确定
如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,如图所示的这种方法,是利用了三角形全等中的
A. SSS B. ASA C. AAS D. SAS
如图,要测量河中礁石A离岸边B点的距离,采取的方法如下:顺着河岸的方向任作一条线段BC,作,可得≌,所以,所以测量的长即可得AB的长,判定图中两个三角形全等的理由是
A. SAS B. ASA C. SSS D. AAS
如图所示,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带去.
A. B. C. D.
茗茗用同种材料制成的金属框架如图所示,已知,,,其中的周长为24cm,,则制成整个金属框架所需这种材料的长度为
A. 51cm B. 48cm C. 45cm D. 54cm
如图,,若,,则AB的长为? ? ?
A. 6 B. 5 C. 4 D. 3
如图,两棵大树间相距13m,小华从点B沿BC走向点C,行走一段时间后他到达点E,此时他仰望两棵大树的顶点A和D,两条视线的夹角正好为,且已知大树AB的高为5m,小华行走的速度为,小华走的时间是
A. 13s B. 8s C. 6s D. 5s
在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中,,测得,,圆形容器的壁厚是? ? ?
A. a B. b C. D.
如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC与右边滑梯水平方向的宽度DF相等,则这两个滑梯与墙面的夹角与的度数和为
A. B. C. D.
如图,将两根钢条、的中点O连在一起,使、能绕着点O自由转动,就做成了一个测量工具,由三角形全等可知的长等于内槽宽AB,那么判定≌的理由是
A. SAS B. ASA C. SSS D. AAS
二、填空题
如图,,,,则A、B两点间的距离________.
如图,要测量池塘两岸相对的两点A、B的距离,可以在AB的垂线BF上取两点C、D,使,再作出BF的垂线DE,使A、C、E三点在一条直线上,这时测得______的长就等于AB的长.
现有A、B两个大型储油罐,它们相距2km,计划修建一条笔直的输油管道,使得A、B两个储油罐到输油管道所在直线的距离都为,输油管道所在直线符合上述要求的设计方案有______种.
如图,有两个长度相等的滑梯BC和EF,,则当______时,可以得出左边滑梯的高度AC与右边滑梯水平方向的长度DF相等.
如图,幼儿园的滑梯中有两个长度相等的梯子,左边滑梯的高度AC等于右边滑梯水平方向的长度DF,则________.
如图,把一长一短两根细木棍的一端用螺钉铰合在一起,使长木棍的另一端与射线BC的端点B重合,固定住长木棍,把短木棍摆动,端点落在射线BC上的C、D两位置时,形成和此时,,,但是和不全等,这说明______.
如图,是小明荡秋千的侧面示意图,秋千链长秋千踏板视作一个点,静止时秋千位于铅垂线BC上,此时秋千踏板到地面的距离为当秋千踏板摆动到点D时,点D到BC的距离若他从D处摆动到处时,恰好,则到地面的距离为__________m.
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中,,晓明同学在探究筝形的性质时,得到如下结论:≌;;;其中,正确的结论有______个.
如图,在中,,点M在线段AB上,,,垂足为G,MG与BC交于点若,则________cm.
课间,小聪拿着老师的等腰直角三角板玩,不小心掉到两墙之间如图,,,每块砌墙用的砖块厚度为8cm,小聪很快就知道了两个墙脚之间的距离DE的长为______cm.
三、解答题
小强为了测量一幢高楼AB的高度,在旗杆CD与楼之间选定一点测得旗杆顶C视线PC与地面夹角,测得楼顶A视线PA与地面夹角,量得P到楼底距离PB与旗杆高度相等,等于10米,量得旗杆与楼之间距离为米,小强计算出了楼高,楼高AB是多少米?
某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得河的宽度,他们是这样做的:
在河流的一条岸边B点,选对岸正对的一棵树A;
沿河岸直走20m有一树C,继续前行20m到达D处;
从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;
测得DE的长为5米.
求:河的宽度是多少米?
请你证明他们做法的正确性.
【答案】
1. B 2. D 3. B 4. D 5. C 6. D 7. B
8. D 9. C 10. A
11. 20m??
12. DE??
13. 4??
14. 63??
15. ??
16. 两边及一边对角对应相等的两个三角形不一定全等??
17. ??
18. 3??
19. 4??
20. 56??
21. 解:,,,
.
在和中,
≌.
.
米,米,
米.
答:楼高AB是26米.??
22. 解:河的宽度是5m;
证明:由作法知,,,
在和中,
,
≌,
,
即他们的做法是正确的.??
第2页,共2页
第1页,共1页
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
