2020年中考 完全平方公式、分母有理化、因式分解 专项练习(无答案)
文档属性
| 名称 | 2020年中考 完全平方公式、分母有理化、因式分解 专项练习(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 131.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-15 07:45:57 | ||
图片预览

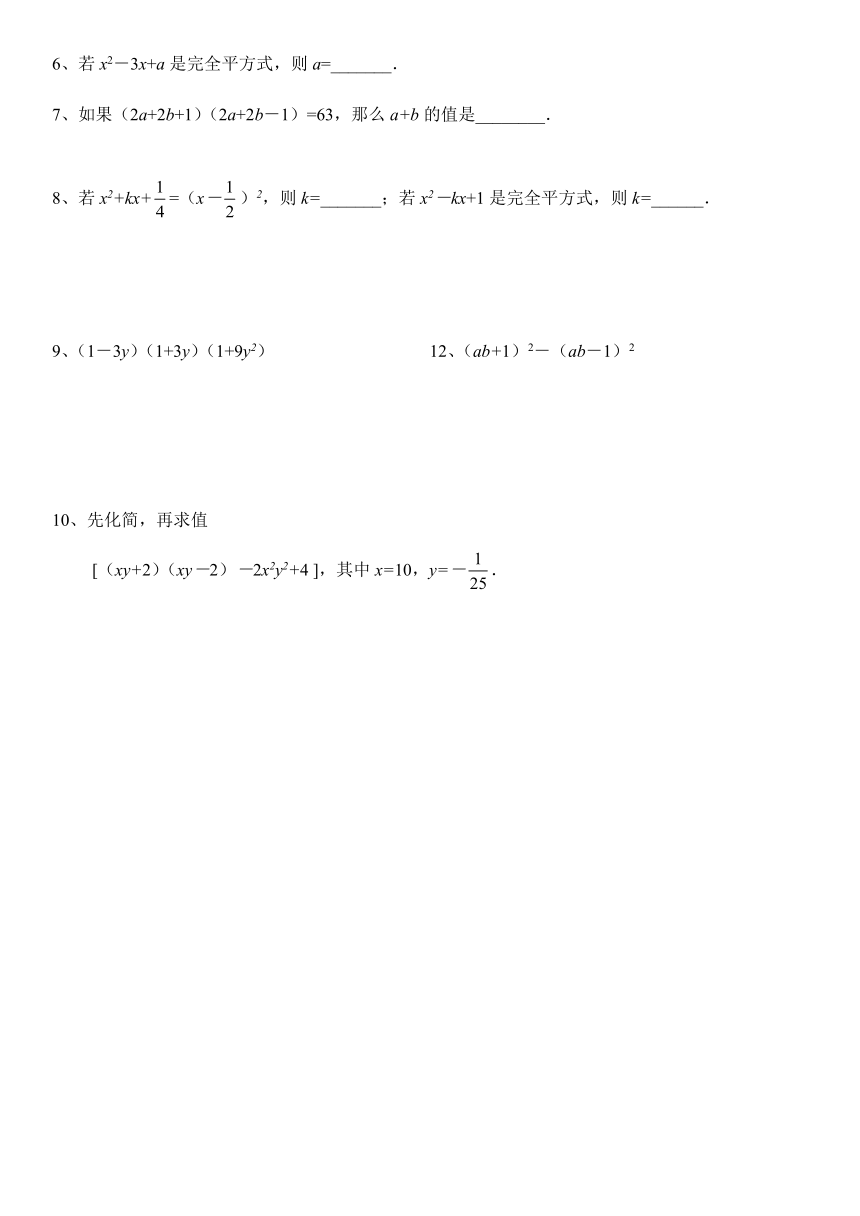

文档简介
完全平方公式、分母有理化、因式分解
教学目标
1、掌握完全平方公式和平方差公式;
2、知道如何化简分式,进行分母有理化;
3、学会因式分解,掌握因式分解的技巧。
教学内容
识点一:完全平方公式,平方差公式
乘法公式:
(1)平方差公式: (a+b)(a-b)=a2-b2 ;(2)完全平方公式: (a±b)2=a2±2ab+b2 .
课堂引入:运用乘法公式简便计算
(998)2 197×203
例题1:
1、19922-19912=____________.
2、
课堂检测:
1、若(x-2y)2=(x+2y)2+m,则m等于( ).
A.4xy B.-4xy C.8xy D.-8xy
2、(a-b+c)(-a+b-c)等于( ).
A.-(a-b+c)2 B.c2-(a-b)2 C.(a-b)2-c D.c2-a+b2
4、下列多项式乘法算式中,可以用平方差公式计算的是( ).
A.(m-n)(n-m) B.(a+b)(-a-b)
C.(-a-b)(a-b) D.(a+b)(a+b)
5、下列等式恒成立的是( ).
A.(m+n)2=m2+n2 B.(2a-b)2=4a2-2ab+b2
C.(4x+1)2=16x2+8x+1 D.(x-3)2=x2-9
若x2-3x+a是完全平方式,则a=_______.
如果(2a+2b+1)(2a+2b-1)=63,那么a+b的值是________.
若x2+kx+=(x-)2,则k=_______;若x2-kx+1是完全平方式,则k=______.
9、(1-3y)(1+3y)(1+9y2) 12、(ab+1)2-(ab-1)2
10、先化简,再求值
[(xy+2)(xy-2)-2x2y2+4 ],其中x=10,y=-.
知识点二:根式分母有理化
1.分母有理化
定义:把分母中的根号化去,叫做分母有理化。
2.有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,就说这两个代数式互为有理化因式。有理化因式确定方法如下:
①单项二次根式:利用来确定,如:,,与等分别互为有理化因式。
②两项二次根式:利用平方差公式来确定。如与,,分别互为有理化因式。
3.分母有理化的方法与步骤:
(1)先将分子、分母化成最简二次根式;
(2)将分子、分母都乘以分母的有理化因式,使分母中不含根式;
(3)最后结果必须化成最简二次根式或有理式。
例题2:
1、找出下列各式的有理化因式
2、把下列各式分母有理化
3、把下列各式分母有理化:
(1)
(3) (4)
4、计算
5、已知,,求的值
6、化简并求值:,其中,
课堂检测:
1.找出下列各式的有理化因式
2.把下列各式分母有理化
3.计算
4.比较大小与
5.已知,求的值。
6.已知,,求的值。
7.已知,,求下列各式的值:(1)(2)
知识点三:因式分解
例题3:
(一)提取公因式法 (二)公式法
1、 4、
2、 5、
3、 6、
(三)十字相乘法 (四)分组分解法
7、 10、
8、 11、
9、 12、.
课堂检测:
1、 8a4b3-4a3b4+2a2b5 2、-9ab+18a2b2-27a3b3
3、(x+y)2-4(x-y)2 4、4x2-20xy+25y2
(a+b)2+10c(a+b)+25c2 6、
8、
9、 10、
教学目标
1、掌握完全平方公式和平方差公式;
2、知道如何化简分式,进行分母有理化;
3、学会因式分解,掌握因式分解的技巧。
教学内容
识点一:完全平方公式,平方差公式
乘法公式:
(1)平方差公式: (a+b)(a-b)=a2-b2 ;(2)完全平方公式: (a±b)2=a2±2ab+b2 .
课堂引入:运用乘法公式简便计算
(998)2 197×203
例题1:
1、19922-19912=____________.
2、
课堂检测:
1、若(x-2y)2=(x+2y)2+m,则m等于( ).
A.4xy B.-4xy C.8xy D.-8xy
2、(a-b+c)(-a+b-c)等于( ).
A.-(a-b+c)2 B.c2-(a-b)2 C.(a-b)2-c D.c2-a+b2
4、下列多项式乘法算式中,可以用平方差公式计算的是( ).
A.(m-n)(n-m) B.(a+b)(-a-b)
C.(-a-b)(a-b) D.(a+b)(a+b)
5、下列等式恒成立的是( ).
A.(m+n)2=m2+n2 B.(2a-b)2=4a2-2ab+b2
C.(4x+1)2=16x2+8x+1 D.(x-3)2=x2-9
若x2-3x+a是完全平方式,则a=_______.
如果(2a+2b+1)(2a+2b-1)=63,那么a+b的值是________.
若x2+kx+=(x-)2,则k=_______;若x2-kx+1是完全平方式,则k=______.
9、(1-3y)(1+3y)(1+9y2) 12、(ab+1)2-(ab-1)2
10、先化简,再求值
[(xy+2)(xy-2)-2x2y2+4 ],其中x=10,y=-.
知识点二:根式分母有理化
1.分母有理化
定义:把分母中的根号化去,叫做分母有理化。
2.有理化因式:两个含有二次根式的代数式相乘,如果它们的积不含有二次根式,就说这两个代数式互为有理化因式。有理化因式确定方法如下:
①单项二次根式:利用来确定,如:,,与等分别互为有理化因式。
②两项二次根式:利用平方差公式来确定。如与,,分别互为有理化因式。
3.分母有理化的方法与步骤:
(1)先将分子、分母化成最简二次根式;
(2)将分子、分母都乘以分母的有理化因式,使分母中不含根式;
(3)最后结果必须化成最简二次根式或有理式。
例题2:
1、找出下列各式的有理化因式
2、把下列各式分母有理化
3、把下列各式分母有理化:
(1)
(3) (4)
4、计算
5、已知,,求的值
6、化简并求值:,其中,
课堂检测:
1.找出下列各式的有理化因式
2.把下列各式分母有理化
3.计算
4.比较大小与
5.已知,求的值。
6.已知,,求的值。
7.已知,,求下列各式的值:(1)(2)
知识点三:因式分解
例题3:
(一)提取公因式法 (二)公式法
1、 4、
2、 5、
3、 6、
(三)十字相乘法 (四)分组分解法
7、 10、
8、 11、
9、 12、.
课堂检测:
1、 8a4b3-4a3b4+2a2b5 2、-9ab+18a2b2-27a3b3
3、(x+y)2-4(x-y)2 4、4x2-20xy+25y2
(a+b)2+10c(a+b)+25c2 6、
8、
9、 10、
同课章节目录
