高一年级下册数学课件 同角三角函数的基本关系式的应用 人教B版(35张ppt)
文档属性
| 名称 | 高一年级下册数学课件 同角三角函数的基本关系式的应用 人教B版(35张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 02:12:52 | ||
图片预览





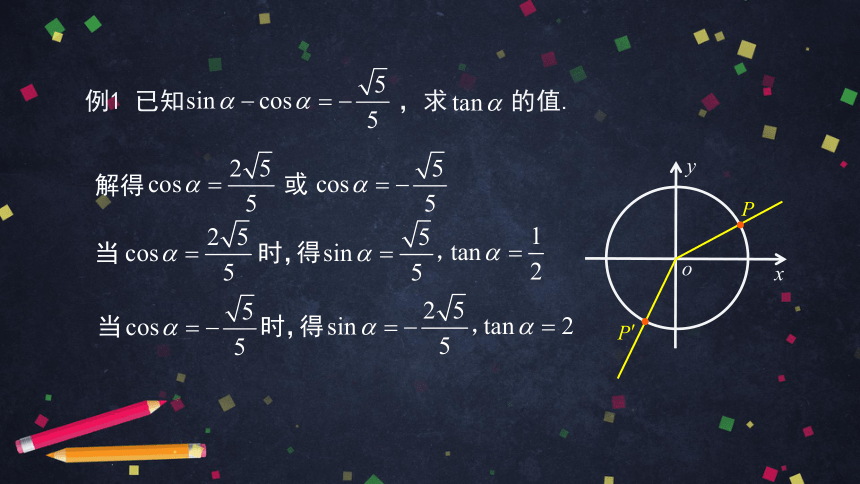




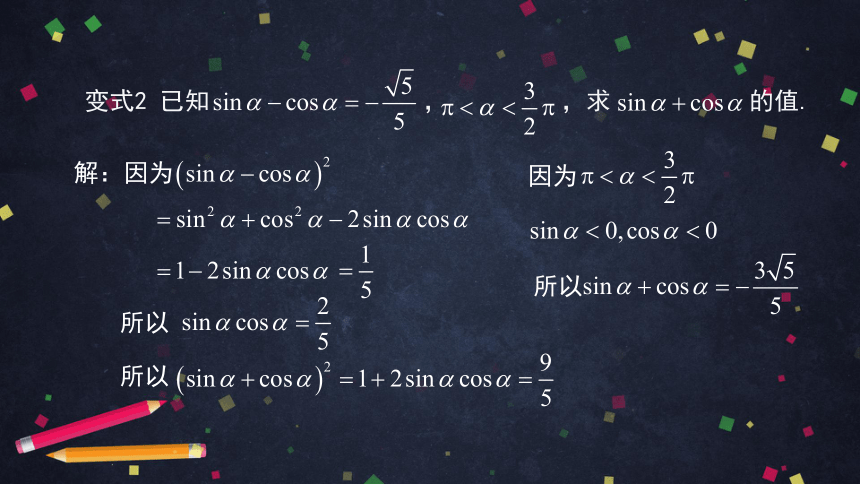
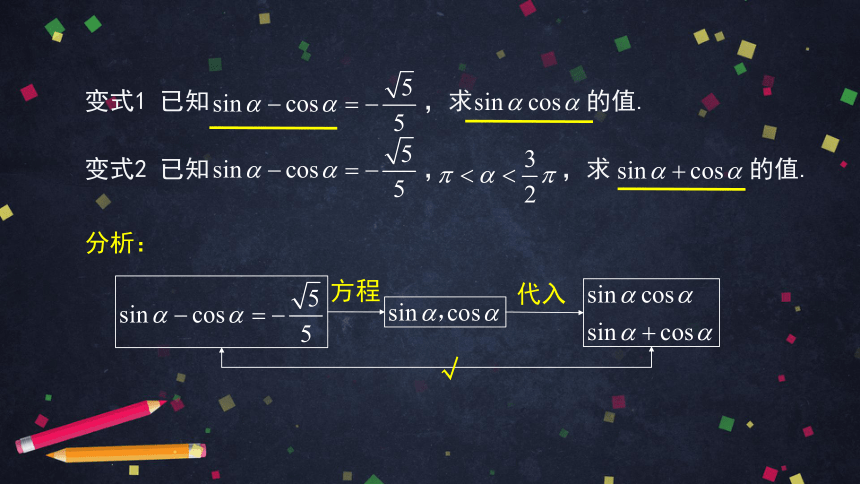
文档简介
(共35张PPT)
同角三角函数的基本关系式的应用
高一年级 数学
回顾:同角三角函数的基本关系式
y
o
x
回顾:同角三角函数值知一求其他
二次方程(组)
两个终边位置
数
形
y
o
x
例1 已知 ,求 的值.
分析:方程思想
解方程组求解
y
o
x
例1 已知 ,求 的值.
解:由题意和同角三角函数的基本关系式,有
,解得
消去 得
或
y
o
x
例1 已知 ,求 的值.
解得
y
o
x
或
当 时,
得
当 时,
得
变式1 已知 ,求 的值.
分析:
2.两个代数式直接建立联系
1.方程思想
变式1 已知 ,求 的值.
解:已知平方得
所以
解得
变式1 已知 ,求 的值.
解:已知平方得
所以
解得
1.方程思想
2.两个代数式直接建立联系
或
解:
解得
变式2 已知 , ,求 的值.
分析:
两个代数式可以建立联系吗?
变式2 已知 , ,求 的值.
解:因为
所以
所以
因为
所以
变式1 已知 ,求 的值.
变式2 已知 , ,求 的值.
分析:
√
方程
代入
变式3 已知 ,求 的值.
分析:两个代数式可以建立联系吗?
?
方程
代入
回顾:
无理式
有理式
分式
整式
不合并
合并
何为简?
如何理解三角式?
角
三角函数名
代数结构
……
例2 化简
例2 化简
分析:
商数关系
三个函数名
一个角、三个函数名、一次分式结构
两个函数名
代数运算
化简结果
例2 化简
分析:
商数关系
正弦
一个角、三个函数名、一次分式结构
余弦、正切
解:
例2 化简
分析:
商数关系
正切
一个角、三个函数名、一次分式结构
正弦、余弦
解:
例2 化简
商数关系
余弦
正弦、正切
解:
分析:
当 时,
当 时,
因此,
理解
三角式
角
三角函数名
代数结构
三角式化简
掌握
运算法则
探究
运算思路
求得
运算结果
同角三角函数的基本关系式
函数名转化
代数运算
例3 求证
一边变形至另一边
两边同时变形
作差法
分析法
证明恒等式
综合法
例3 求证
分析:
一个角、两个函数名、二次、四次
证明:
原式左边
右边
因此
思路:由繁到简
例3 求证
分析:
一个角、两个函数名、二次
证明:
原式左边
右边
因此
思路:差→积
例3 求证
分析:
一个角、两个函数名、二次
证明:
原式右边
左边
因此
思路:积→差
例3 求证
分析:
一个角、两个函数名、一次分式
证明:
因此
思路:做差
例3 求证
思考:
这样的做法正确吗?
证明: 由
上式成立,因此
得
错误
例3 求证
逻辑顺序相反
正解:
条件
错解:
条件
思考:
这样的做法正确吗?
例3 求证
正解:
分析法
证明: 要证
只需证
只需证
因为上式成立,所以
例3 求证
正解:
分析法寻找证明思路,综合法写证明过程
证明: 因为
因此
由题知
小结:同角三角函数的基本关系式的应用
1.应用同角三角函数的基本关系式求值、化简、证明;
理解
运算对象
掌握
运算法则
探究
运算思路
求得
运算结果
小结:同角三角函数的基本关系式的应用
2.利用同角关系式得到新的恒等式.
作业:
(1) ;
1.已知 ,求下列各式的值.
(2) ;
(3) .
作业:
(1) ;
2.化简.
(2) ;
(3) ;
(4) .
作业:
(1) ;
3.求证:
(2) ;
(3) .
感谢观看
同角三角函数的基本关系式的应用
高一年级 数学
回顾:同角三角函数的基本关系式
y
o
x
回顾:同角三角函数值知一求其他
二次方程(组)
两个终边位置
数
形
y
o
x
例1 已知 ,求 的值.
分析:方程思想
解方程组求解
y
o
x
例1 已知 ,求 的值.
解:由题意和同角三角函数的基本关系式,有
,解得
消去 得
或
y
o
x
例1 已知 ,求 的值.
解得
y
o
x
或
当 时,
得
当 时,
得
变式1 已知 ,求 的值.
分析:
2.两个代数式直接建立联系
1.方程思想
变式1 已知 ,求 的值.
解:已知平方得
所以
解得
变式1 已知 ,求 的值.
解:已知平方得
所以
解得
1.方程思想
2.两个代数式直接建立联系
或
解:
解得
变式2 已知 , ,求 的值.
分析:
两个代数式可以建立联系吗?
变式2 已知 , ,求 的值.
解:因为
所以
所以
因为
所以
变式1 已知 ,求 的值.
变式2 已知 , ,求 的值.
分析:
√
方程
代入
变式3 已知 ,求 的值.
分析:两个代数式可以建立联系吗?
?
方程
代入
回顾:
无理式
有理式
分式
整式
不合并
合并
何为简?
如何理解三角式?
角
三角函数名
代数结构
……
例2 化简
例2 化简
分析:
商数关系
三个函数名
一个角、三个函数名、一次分式结构
两个函数名
代数运算
化简结果
例2 化简
分析:
商数关系
正弦
一个角、三个函数名、一次分式结构
余弦、正切
解:
例2 化简
分析:
商数关系
正切
一个角、三个函数名、一次分式结构
正弦、余弦
解:
例2 化简
商数关系
余弦
正弦、正切
解:
分析:
当 时,
当 时,
因此,
理解
三角式
角
三角函数名
代数结构
三角式化简
掌握
运算法则
探究
运算思路
求得
运算结果
同角三角函数的基本关系式
函数名转化
代数运算
例3 求证
一边变形至另一边
两边同时变形
作差法
分析法
证明恒等式
综合法
例3 求证
分析:
一个角、两个函数名、二次、四次
证明:
原式左边
右边
因此
思路:由繁到简
例3 求证
分析:
一个角、两个函数名、二次
证明:
原式左边
右边
因此
思路:差→积
例3 求证
分析:
一个角、两个函数名、二次
证明:
原式右边
左边
因此
思路:积→差
例3 求证
分析:
一个角、两个函数名、一次分式
证明:
因此
思路:做差
例3 求证
思考:
这样的做法正确吗?
证明: 由
上式成立,因此
得
错误
例3 求证
逻辑顺序相反
正解:
条件
错解:
条件
思考:
这样的做法正确吗?
例3 求证
正解:
分析法
证明: 要证
只需证
只需证
因为上式成立,所以
例3 求证
正解:
分析法寻找证明思路,综合法写证明过程
证明: 因为
因此
由题知
小结:同角三角函数的基本关系式的应用
1.应用同角三角函数的基本关系式求值、化简、证明;
理解
运算对象
掌握
运算法则
探究
运算思路
求得
运算结果
小结:同角三角函数的基本关系式的应用
2.利用同角关系式得到新的恒等式.
作业:
(1) ;
1.已知 ,求下列各式的值.
(2) ;
(3) .
作业:
(1) ;
2.化简.
(2) ;
(3) ;
(4) .
作业:
(1) ;
3.求证:
(2) ;
(3) .
感谢观看
