高一年级下册数学课件同角三角函数的基本关系式 人教B版(27张ppt)
文档属性
| 名称 | 高一年级下册数学课件同角三角函数的基本关系式 人教B版(27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 00:00:00 | ||
图片预览






文档简介
(共27张PPT)
同角三角函数的基本关系式
高一年级 数学
y
o
x
回顾:三角函数的定义
设角 的终边与单位圆的交点为 ,
y
o
x
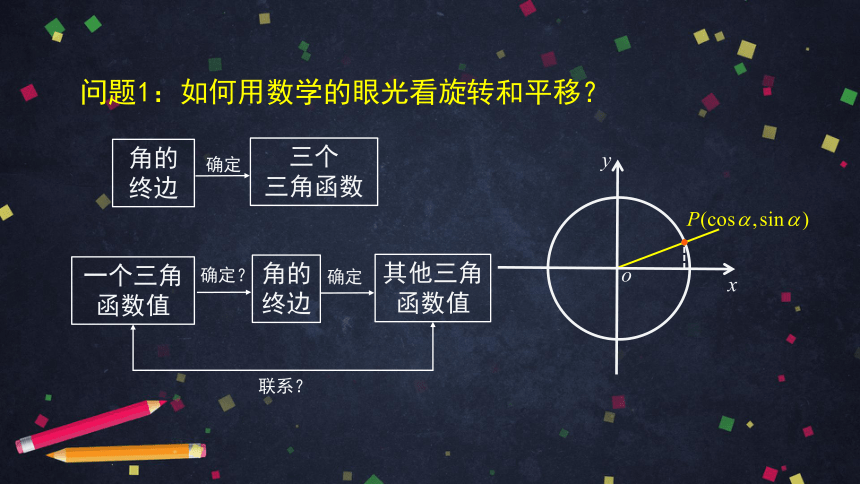
问题1:如何用数学的眼光看旋转和平移?
确定
角的终边
三个
三角函数
一个三角函数值
角的终边
其他三角函数值
联系?
确定?
确定
问题1:如何用数学的眼光看旋转和平移?
终边 :旋转过程中,
的坐标发生变化,
但与原点距离保持不变
y
o
x
单位圆:圆心 ,半径
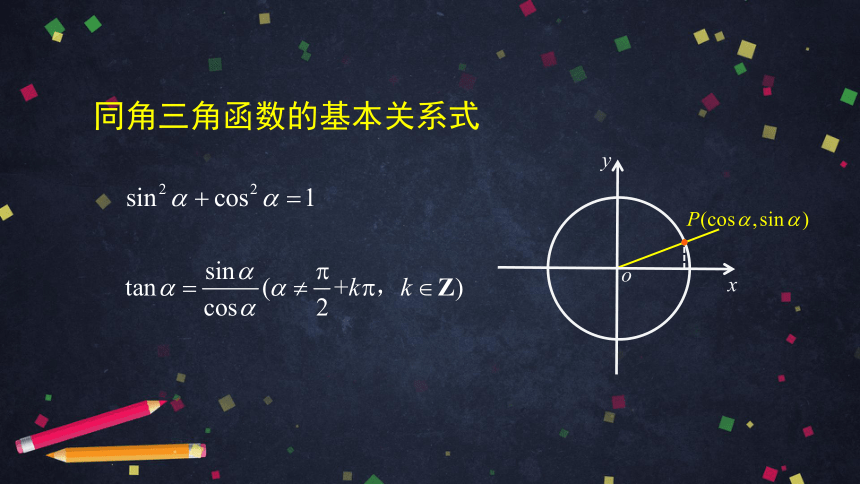
同角三角函数的基本关系式
y
o
x
静态:
方程
(二元二次)
功能(知一求一)
两组解?
两个终边位置
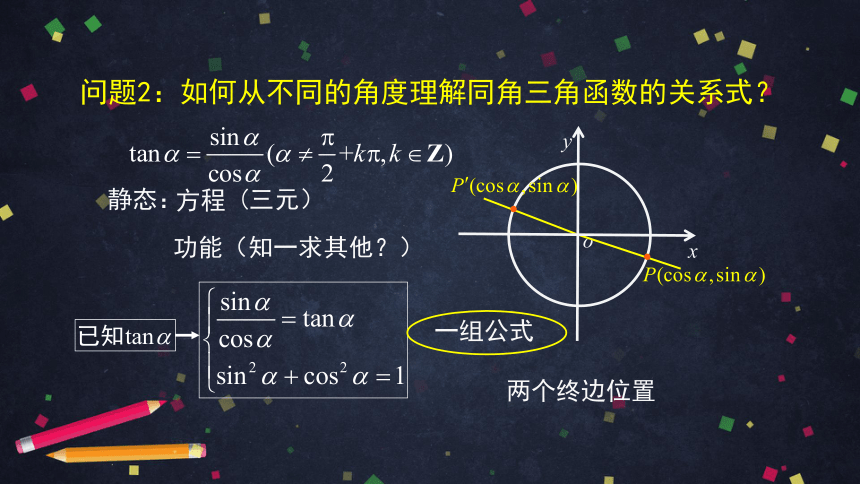
问题2:如何从不同的角度理解同角三角函数的关系式?
y
o
x
静态:
方程
(三元)
功能(知一求其他?)
两个终边位置
一组公式
问题2:如何从不同的角度理解同角三角函数的关系式?
o
y
x
动态:
两个函数的关系
三个函数的关系
问题2:如何从不同的角度理解同角三角函数的关系式?
例1 已知 ,且 是第二象限角,求角 的余弦和正切.
数
分析:
问题3:同角的三角函数值中,已知一个能求出其他吗?
y
o
x
形
P点纵坐标为 ,角 在第二象限,
余弦和正切值唯一.
y
o
x
解:由
得
因为α是第二象限角,
所以
问题3:同角的三角函数值中,已知一个能求出其他吗?
例1 已知 ,且 是第二象限角,求角 的余弦和正切.
y
x
变式:已知 ,求角 的余弦和正切.
数
分析:
形
一个正弦值对应两个终边位置
余弦和正切不唯一
问题3:同角的三角函数值中,已知一个能求出其他吗?
o
变式:已知 ,求角 的余弦和正切.
问题3:同角的三角函数值中,已知一个能求出其他吗?
解:由
得
若 是第二象限角,
所以
若 是第一象限角,
所以
y
x
o
变式:已知 ,求角 的余弦和正切.
问题3:同角的三角函数值中,已知一个能求出其他吗?
解:由
得
所以
×
y
x
o
分析:
y
x
代入消元
思路1 方程思想
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
利用角所在象限求出唯一正弦、余弦
o
解:由题意和同角三角函数的基本关系式,有
①
②
,代入①解得
由②得
因为α是第二象限角,
,代入②得
y
x
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
o
得到 与 关系
y
x
分析:
思路2 找到已知和所求的二元关系?
得到 与 关系
三元
二元
(新的恒等式)
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
o
即 ,
解:由同角三角函数的基本关系式,
①
②
代入①得
得
y
x
因为α是第二象限角,
所以 , .
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
o
思考:能否将所求化为只含有正切的代数式?
变式 已知 ,求 .
y
x
分析:
思路1 方程思想
思路2 转化
?
o
思考:能否将所求化为只含有正切的代数式?
变式 已知 ,求 .
(分子分母同时
除以 )
y
x
分析:
思路1 方程思想
思路2 转化
(分母变形)
o
得
变式 已知 ,求 .
解:由同角三角函数的基本关系式,
分子分母同时除以
由题意知
y
x
o
变式 已知 ,求 .
举例:
y
x
只含正切
齐次分式
o
思想 方法
三角函数定义
同角三角函数的基本关系式
旋转不变性
静态
动态
方程
(组)
函数
关系
理解
应用
知一求其他
数形结合
小结:
小结:
如何应用公式解决同角三角函数值知一求其他的问题?
不定象限
单位圆上两个点P
两组三角函数值
单位圆上唯一点P
一组三角函数值
分类讨论
(不需分类讨论)
y
x
确定象限
o
(1)已知 ,且 为第一象限角,求 , ;
作业:
1.求解下列各题.
(2)已知 ,且 为第三象限角,求 , ;
(3)已知 ,且 为第四象限角,求 , ;
(4)已知 ,且 为第二象限角,求 , ;
2.已知 ,求 和 .
作业:
3.已知 ,求 和 .
(1) ;
作业:
4.已知 ,求下列各式的值.
(2) ;
(3) ;
(4) .
感谢观看
同角三角函数的基本关系式
高一年级 数学
y
o
x
回顾:三角函数的定义
设角 的终边与单位圆的交点为 ,
y
o
x
问题1:如何用数学的眼光看旋转和平移?
确定
角的终边
三个
三角函数
一个三角函数值
角的终边
其他三角函数值
联系?
确定?
确定
问题1:如何用数学的眼光看旋转和平移?
终边 :旋转过程中,
的坐标发生变化,
但与原点距离保持不变
y
o
x
单位圆:圆心 ,半径
同角三角函数的基本关系式
y
o
x
静态:
方程
(二元二次)
功能(知一求一)
两组解?
两个终边位置
问题2:如何从不同的角度理解同角三角函数的关系式?
y
o
x
静态:
方程
(三元)
功能(知一求其他?)
两个终边位置
一组公式
问题2:如何从不同的角度理解同角三角函数的关系式?
o
y
x
动态:
两个函数的关系
三个函数的关系
问题2:如何从不同的角度理解同角三角函数的关系式?
例1 已知 ,且 是第二象限角,求角 的余弦和正切.
数
分析:
问题3:同角的三角函数值中,已知一个能求出其他吗?
y
o
x
形
P点纵坐标为 ,角 在第二象限,
余弦和正切值唯一.
y
o
x
解:由
得
因为α是第二象限角,
所以
问题3:同角的三角函数值中,已知一个能求出其他吗?
例1 已知 ,且 是第二象限角,求角 的余弦和正切.
y
x
变式:已知 ,求角 的余弦和正切.
数
分析:
形
一个正弦值对应两个终边位置
余弦和正切不唯一
问题3:同角的三角函数值中,已知一个能求出其他吗?
o
变式:已知 ,求角 的余弦和正切.
问题3:同角的三角函数值中,已知一个能求出其他吗?
解:由
得
若 是第二象限角,
所以
若 是第一象限角,
所以
y
x
o
变式:已知 ,求角 的余弦和正切.
问题3:同角的三角函数值中,已知一个能求出其他吗?
解:由
得
所以
×
y
x
o
分析:
y
x
代入消元
思路1 方程思想
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
利用角所在象限求出唯一正弦、余弦
o
解:由题意和同角三角函数的基本关系式,有
①
②
,代入①解得
由②得
因为α是第二象限角,
,代入②得
y
x
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
o
得到 与 关系
y
x
分析:
思路2 找到已知和所求的二元关系?
得到 与 关系
三元
二元
(新的恒等式)
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
o
即 ,
解:由同角三角函数的基本关系式,
①
②
代入①得
得
y
x
因为α是第二象限角,
所以 , .
例2 已知 ,且 是第二象限角,求角 的正弦和余弦.
o
思考:能否将所求化为只含有正切的代数式?
变式 已知 ,求 .
y
x
分析:
思路1 方程思想
思路2 转化
?
o
思考:能否将所求化为只含有正切的代数式?
变式 已知 ,求 .
(分子分母同时
除以 )
y
x
分析:
思路1 方程思想
思路2 转化
(分母变形)
o
得
变式 已知 ,求 .
解:由同角三角函数的基本关系式,
分子分母同时除以
由题意知
y
x
o
变式 已知 ,求 .
举例:
y
x
只含正切
齐次分式
o
思想 方法
三角函数定义
同角三角函数的基本关系式
旋转不变性
静态
动态
方程
(组)
函数
关系
理解
应用
知一求其他
数形结合
小结:
小结:
如何应用公式解决同角三角函数值知一求其他的问题?
不定象限
单位圆上两个点P
两组三角函数值
单位圆上唯一点P
一组三角函数值
分类讨论
(不需分类讨论)
y
x
确定象限
o
(1)已知 ,且 为第一象限角,求 , ;
作业:
1.求解下列各题.
(2)已知 ,且 为第三象限角,求 , ;
(3)已知 ,且 为第四象限角,求 , ;
(4)已知 ,且 为第二象限角,求 , ;
2.已知 ,求 和 .
作业:
3.已知 ,求 和 .
(1) ;
作业:
4.已知 ,求下列各式的值.
(2) ;
(3) ;
(4) .
感谢观看
