高一年级下册物理 圆周运动 人教版(47张ppt)
文档属性
| 名称 | 高一年级下册物理 圆周运动 人教版(47张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 38.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-05-14 14:29:59 | ||
图片预览






文档简介
(共47张PPT)
圆周运动
高一年级 物理
第六章 圆周运动
第六章 圆周运动
轨迹是圆周或一段圆弧的机械运动叫做圆周运动。
第六章 圆周运动
轨迹是圆周或一段圆弧的机械运动叫做圆周运动。
6.1 圆周运动
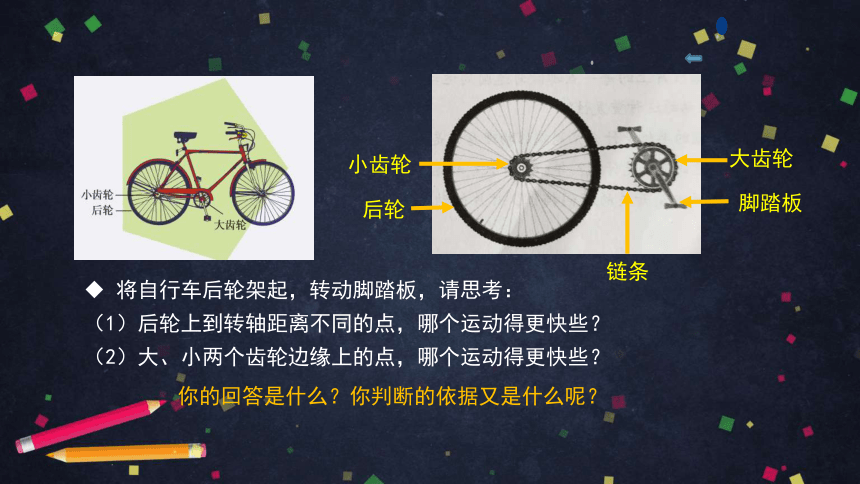
将自行车后轮架起,转动脚踏板,请思考:
(1)后轮上到转轴距离不同的点,哪个运动得更快些?
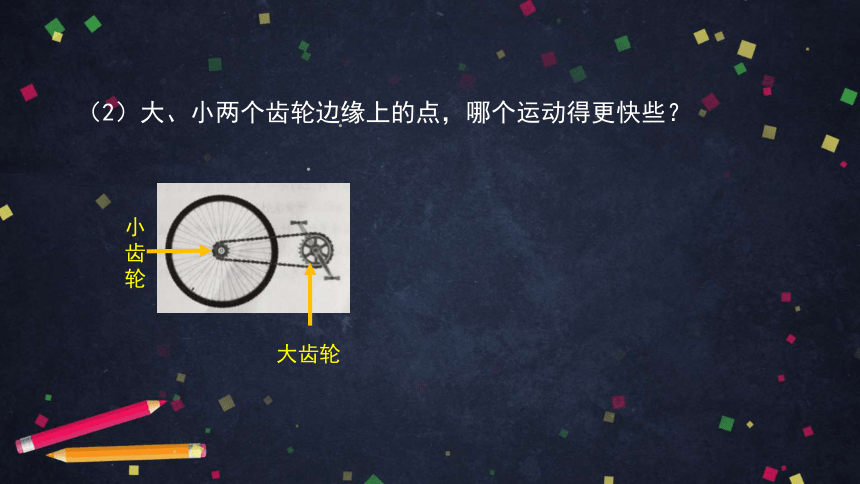
(2)大、小两个齿轮边缘上的点,哪个运动得更快些?
你的回答是什么?你判断的依据又是什么呢?
小齿轮
大齿轮
后轮
脚踏板
链条
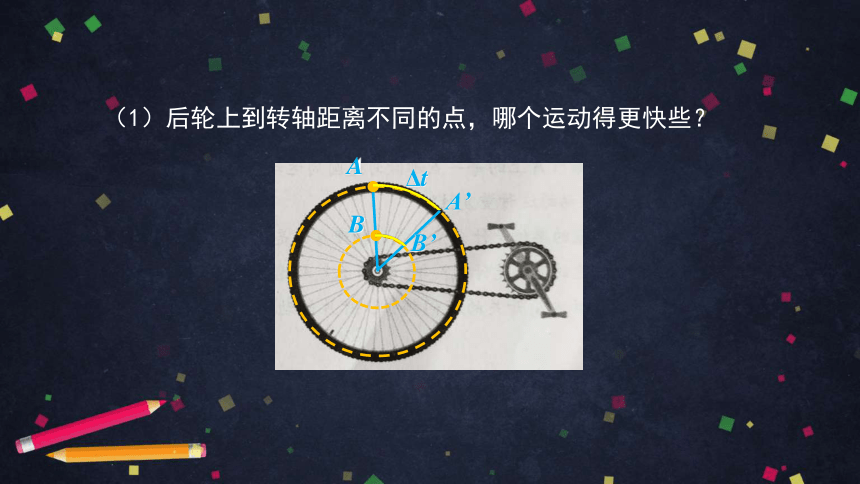
(1)后轮上到转轴距离不同的点,哪个运动得更快些?
B
A
Δt
A’
B’
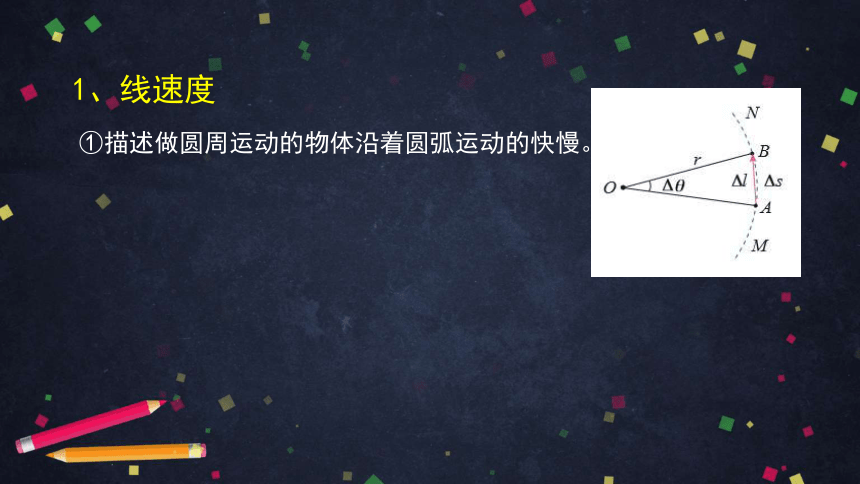
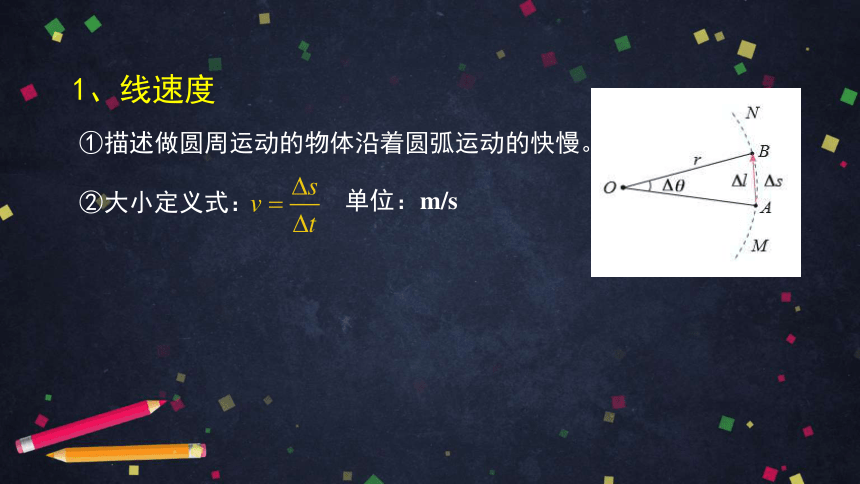
①描述做圆周运动的物体沿着圆弧运动的快慢。
1、线速度
1、线速度
单位:m/s
②大小定义式:
①描述做圆周运动的物体沿着圆弧运动的快慢。
1、线速度
②大小定义式:
单位:m/s
①描述做圆周运动的物体沿着圆弧运动的快慢。
③方向:质点在圆周某点的线速度方向沿
圆周上该点的切线方向(与半径垂直)。
1、线速度
③方向:质点在圆周某点的线速度方向沿
圆周上该点的切线方向(与半径垂直)。
④线速度的大小不变的圆周运动,叫做匀速圆周运动。
注意:匀速圆周运动是变速运动
②大小定义式:
单位:m/s
①描述做圆周运动的物体沿着圆弧运动的快慢。
(2)大、小两个齿轮边缘上的点,哪个运动得更快些?
小齿轮
大齿轮
(2)大、小两个齿轮边缘上的点,哪个运动得更快些?
小齿轮
大齿轮
如何比较大、小齿轮做圆周运动转动的快慢?
1、比较相同时间内转过的角度
1、比较相同时间内转过的角度
2、比较转过一圈所用的时间
3、比较相同时间内转过的圈数
比较做圆周运动的物体转动快慢的方法
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
②定义式:
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
单位:弧度每秒(rad/s)或 s-1
②定义式:
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
说明:匀速圆周运动是角速度不变的圆周运动。
②定义式:
单位:弧度每秒(rad/s)或 s-1
1、比较相同时间内转过的角度
2、比较转过一圈所用的时间
3、比较相同时间内转过的圈数
比较做圆周运动的物体转动快慢的方法
3、周期
①定义:做匀速圆周运动的物体,运动一周所用的时间。
符号:T 单位:秒(s)
②大小:
3、周期
①定义:做匀速圆周运动的物体,运动一周所用的时间。
符号:T 单位:秒(s)
②大小:
3、周期
①定义:做匀速圆周运动的物体,运动一周所用的时间。
符号:T 单位:秒(s)
1、比较相同时间内转过的角度
2、比较转过一圈所用的时间
3、比较相同时间内转过的圈数
比较做圆周运动的物体转动快慢的方法
4、转速:物体转动的圈数与所用时间的比值
符号:n
4、转速:物体转动的圈数与所用时间的比值
符号:n
单位:转每秒(r/s) 或者 转每分(r/min)
角速度与转速的关系:
4、转速:物体转动的圈数与所用时间的比值
符号:n
单位:转每秒(r/s) 或者 转每分(r/min)
知识梳理
1、线速度
2、角速度
3、周期
4、转速
从不同的角度描述做圆周运动的物体绕圆心转动的快慢
描述做圆周运动的物体沿着圆弧运动的快慢
Δs
A’
A
Δs
A’
A
转动的慢
转动的快
Δθ
Δθ
5、线速度与角速度的关系:
角速度
由于线速度
Δt
在右图中,设物体做圆周运动的半径为r,由A运动到B的时间为Δt,AB弧的弧长为Δs,AB弧对应的圆心角为Δθ。
由此可得
当以弧度为单位时 或
例题1
一个小孩坐在游乐场的旋转木马上,绕中心轴在水平面内做匀速圆周运动,圆周的半径为4.0m。当他的线速度为2.0 m/s 时,他做匀速圆周运动的角速度是多少?周期是多少?
解:当小孩的线速度为 2.0 m/s 时,他做匀速圆周运动的角速度
例题1
他做匀速圆周运动的周期
一个小孩坐在游乐场的旋转木马上,绕中心轴在水平面内做匀速圆周运动,圆周的半径为4.0m。当他的线速度为2.0 m/s 时,他做匀速圆周运动的角速度是多少?周期是多少?
解:当小孩的线速度为 2.0 m/s 时,他做匀速圆周运动的角速度
例题2
如图所示,A、B 两点分别位于大、 小轮的边缘上,C 点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动, 接触面上没有滑动。请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
(1)v相等,ω跟r成反比。
(2)ω相等,v跟r成正比。
(3)r 相等,v跟ω成正比。
观察齿轮传动的特点
例题2
(1)v相等,ω跟r成反比。
A、B两点v相等,ω与r成反比
ωA: ωB=rB:rA=1:2
请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
例题2
请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
(2)ω相等,v跟r成正比。
A、C两点ω相等,v与r成正比
vA: vC=rA:rC=2:1
例题2
请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
(3)r 相等,v跟ω成正比。
B、C 两点r相等,v 跟ω成正比
vB:vC=vA: vC= rA: rC =2:1
ωB: ωC =ωB: ωA=rA: rB=2:1
vB:vC=ωB: ωC
齿轮传动在生活中的应用
小齿轮
大齿轮
后轮
脚踏板
如图所示是自行车传动机构的示意图。假设脚踏板转动的周期是T,要知道在这种情况下自行车前进的速度有多大,还需要测量哪些量?请用这些量推导出自行车前进速度的表达式。
*例题3
*例题3
轮轴
v
以轮轴为参考系分析:
车轮:圆周运动
地面:向左运动
v
猜测:观察下面三辆自行车,在脚踏板周期一定的情况下,自行车前进速度可能和哪些物理量有关?
车轮直径14英寸
约36cm
车轮直径24英寸
约61cm
车轮直径26英寸
约66cm
理论分析
测后轮的线速度?
脚踏板的周期
v=ωr
答案:测量后轮的半径,大小齿轮的半径或者半径比
脚踏板的角速度
后轮半径
后轮的角速度
小齿轮的角速度
大齿轮角速度
大、小齿轮的半径或者半径比
解:已知脚踏板的周期为T,大小齿轮和后轮的半径测量量分别为r1,r2,r3,角速度分别设为ω1,ω2,ω3。根据分析可知:
大齿轮的角速度:
因为大、小齿轮线速度相等,根据 ,可知
又因为车后轮和小齿轮角速度相等:
*例题3
所以后轮的线速度:
自行车前进速度的表达式
车轮直径14英寸
约36cm
车轮直径24英寸
约61cm
车轮直径26英寸
约66cm
小结
圆周运动与匀速圆周运动
线速度与角速度
周期与转速
圆周运动
高一年级 物理
第六章 圆周运动
第六章 圆周运动
轨迹是圆周或一段圆弧的机械运动叫做圆周运动。
第六章 圆周运动
轨迹是圆周或一段圆弧的机械运动叫做圆周运动。
6.1 圆周运动
将自行车后轮架起,转动脚踏板,请思考:
(1)后轮上到转轴距离不同的点,哪个运动得更快些?
(2)大、小两个齿轮边缘上的点,哪个运动得更快些?
你的回答是什么?你判断的依据又是什么呢?
小齿轮
大齿轮
后轮
脚踏板
链条
(1)后轮上到转轴距离不同的点,哪个运动得更快些?
B
A
Δt
A’
B’
①描述做圆周运动的物体沿着圆弧运动的快慢。
1、线速度
1、线速度
单位:m/s
②大小定义式:
①描述做圆周运动的物体沿着圆弧运动的快慢。
1、线速度
②大小定义式:
单位:m/s
①描述做圆周运动的物体沿着圆弧运动的快慢。
③方向:质点在圆周某点的线速度方向沿
圆周上该点的切线方向(与半径垂直)。
1、线速度
③方向:质点在圆周某点的线速度方向沿
圆周上该点的切线方向(与半径垂直)。
④线速度的大小不变的圆周运动,叫做匀速圆周运动。
注意:匀速圆周运动是变速运动
②大小定义式:
单位:m/s
①描述做圆周运动的物体沿着圆弧运动的快慢。
(2)大、小两个齿轮边缘上的点,哪个运动得更快些?
小齿轮
大齿轮
(2)大、小两个齿轮边缘上的点,哪个运动得更快些?
小齿轮
大齿轮
如何比较大、小齿轮做圆周运动转动的快慢?
1、比较相同时间内转过的角度
1、比较相同时间内转过的角度
2、比较转过一圈所用的时间
3、比较相同时间内转过的圈数
比较做圆周运动的物体转动快慢的方法
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
②定义式:
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
单位:弧度每秒(rad/s)或 s-1
②定义式:
①描述做圆周运动的物体绕圆心转动的快慢。
2、角速度
Δt
说明:匀速圆周运动是角速度不变的圆周运动。
②定义式:
单位:弧度每秒(rad/s)或 s-1
1、比较相同时间内转过的角度
2、比较转过一圈所用的时间
3、比较相同时间内转过的圈数
比较做圆周运动的物体转动快慢的方法
3、周期
①定义:做匀速圆周运动的物体,运动一周所用的时间。
符号:T 单位:秒(s)
②大小:
3、周期
①定义:做匀速圆周运动的物体,运动一周所用的时间。
符号:T 单位:秒(s)
②大小:
3、周期
①定义:做匀速圆周运动的物体,运动一周所用的时间。
符号:T 单位:秒(s)
1、比较相同时间内转过的角度
2、比较转过一圈所用的时间
3、比较相同时间内转过的圈数
比较做圆周运动的物体转动快慢的方法
4、转速:物体转动的圈数与所用时间的比值
符号:n
4、转速:物体转动的圈数与所用时间的比值
符号:n
单位:转每秒(r/s) 或者 转每分(r/min)
角速度与转速的关系:
4、转速:物体转动的圈数与所用时间的比值
符号:n
单位:转每秒(r/s) 或者 转每分(r/min)
知识梳理
1、线速度
2、角速度
3、周期
4、转速
从不同的角度描述做圆周运动的物体绕圆心转动的快慢
描述做圆周运动的物体沿着圆弧运动的快慢
Δs
A’
A
Δs
A’
A
转动的慢
转动的快
Δθ
Δθ
5、线速度与角速度的关系:
角速度
由于线速度
Δt
在右图中,设物体做圆周运动的半径为r,由A运动到B的时间为Δt,AB弧的弧长为Δs,AB弧对应的圆心角为Δθ。
由此可得
当以弧度为单位时 或
例题1
一个小孩坐在游乐场的旋转木马上,绕中心轴在水平面内做匀速圆周运动,圆周的半径为4.0m。当他的线速度为2.0 m/s 时,他做匀速圆周运动的角速度是多少?周期是多少?
解:当小孩的线速度为 2.0 m/s 时,他做匀速圆周运动的角速度
例题1
他做匀速圆周运动的周期
一个小孩坐在游乐场的旋转木马上,绕中心轴在水平面内做匀速圆周运动,圆周的半径为4.0m。当他的线速度为2.0 m/s 时,他做匀速圆周运动的角速度是多少?周期是多少?
解:当小孩的线速度为 2.0 m/s 时,他做匀速圆周运动的角速度
例题2
如图所示,A、B 两点分别位于大、 小轮的边缘上,C 点位于大轮半径的中点,大轮的半径是小轮的2倍,它们之间靠摩擦传动, 接触面上没有滑动。请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
(1)v相等,ω跟r成反比。
(2)ω相等,v跟r成正比。
(3)r 相等,v跟ω成正比。
观察齿轮传动的特点
例题2
(1)v相等,ω跟r成反比。
A、B两点v相等,ω与r成反比
ωA: ωB=rB:rA=1:2
请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
例题2
请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
(2)ω相等,v跟r成正比。
A、C两点ω相等,v与r成正比
vA: vC=rA:rC=2:1
例题2
请在该装置的A、B、C 三 个点中选择有关的两个点,说明公式v=ωr 的以下三种变量关系:
(3)r 相等,v跟ω成正比。
B、C 两点r相等,v 跟ω成正比
vB:vC=vA: vC= rA: rC =2:1
ωB: ωC =ωB: ωA=rA: rB=2:1
vB:vC=ωB: ωC
齿轮传动在生活中的应用
小齿轮
大齿轮
后轮
脚踏板
如图所示是自行车传动机构的示意图。假设脚踏板转动的周期是T,要知道在这种情况下自行车前进的速度有多大,还需要测量哪些量?请用这些量推导出自行车前进速度的表达式。
*例题3
*例题3
轮轴
v
以轮轴为参考系分析:
车轮:圆周运动
地面:向左运动
v
猜测:观察下面三辆自行车,在脚踏板周期一定的情况下,自行车前进速度可能和哪些物理量有关?
车轮直径14英寸
约36cm
车轮直径24英寸
约61cm
车轮直径26英寸
约66cm
理论分析
测后轮的线速度?
脚踏板的周期
v=ωr
答案:测量后轮的半径,大小齿轮的半径或者半径比
脚踏板的角速度
后轮半径
后轮的角速度
小齿轮的角速度
大齿轮角速度
大、小齿轮的半径或者半径比
解:已知脚踏板的周期为T,大小齿轮和后轮的半径测量量分别为r1,r2,r3,角速度分别设为ω1,ω2,ω3。根据分析可知:
大齿轮的角速度:
因为大、小齿轮线速度相等,根据 ,可知
又因为车后轮和小齿轮角速度相等:
*例题3
所以后轮的线速度:
自行车前进速度的表达式
车轮直径14英寸
约36cm
车轮直径24英寸
约61cm
车轮直径26英寸
约66cm
小结
圆周运动与匀速圆周运动
线速度与角速度
周期与转速
