高中数学人教B版必修三:7.2.4诱导公式应用 课件(185张ppt)
文档属性
| 名称 | 高中数学人教B版必修三:7.2.4诱导公式应用 课件(185张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 00:00:00 | ||
图片预览





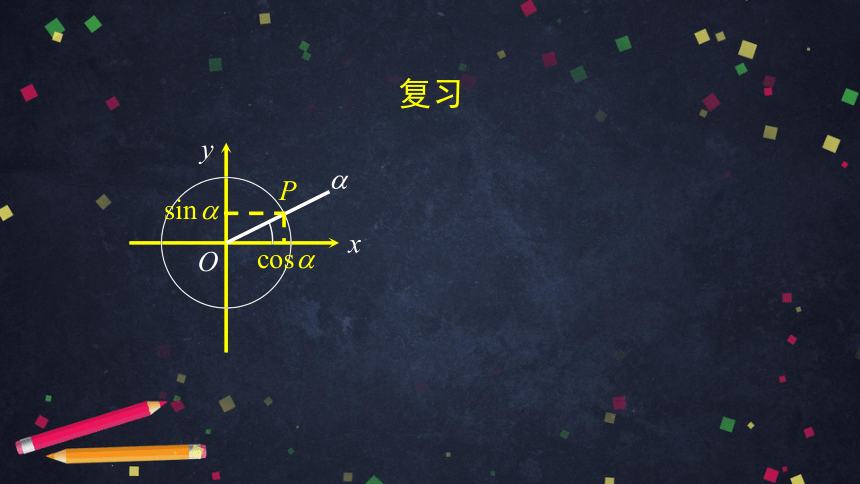
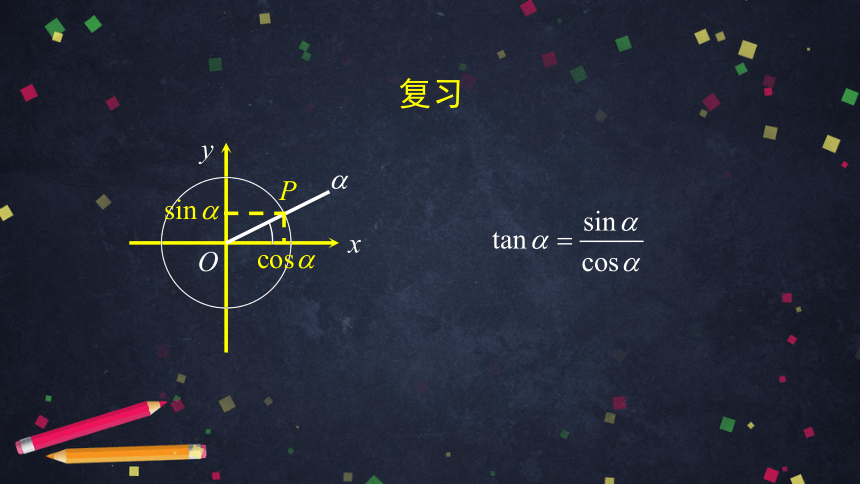




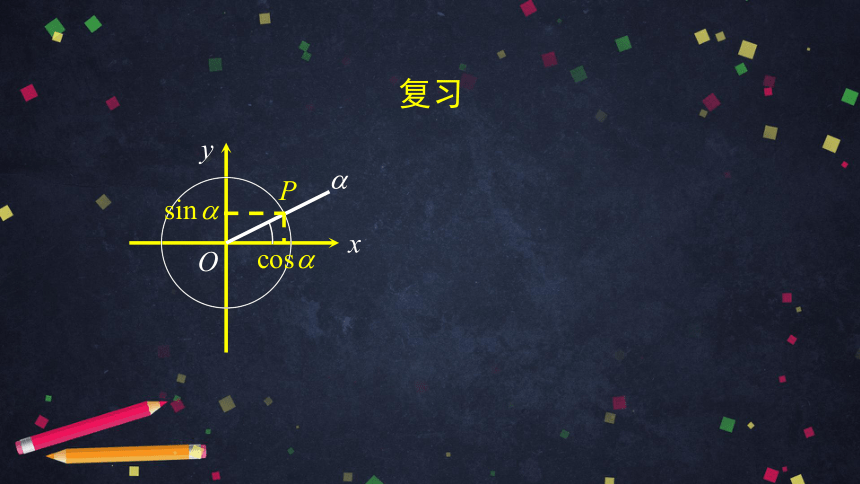
文档简介
(共185张PPT)
高一年级 数学
诱导公式应用
复习
1. 在前两节课中,我们学到了哪些诱导公式 ?
复习
1. 在前两节课中,我们学到了哪些诱导公式 ?
2. 它们是如何得到的 ?
复习
1. 在前两节课中,我们学到了哪些诱导公式 ?
2. 它们是如何得到的 ?
3. 如何利用这些公式求值、化简、证明?
复习
复习
复习
复习
其中
复习
其中
复习
其中
复习
其中
复习
复习
复习
负化正,
利用对称凑锐角.
大化小.
任意负角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
角的
三角函数
复习
负化正,
利用对称凑锐角.
大化小.
复习
负化正,
利用对称凑锐角.
大化小.
角的关系 → 三角函数值的关系
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
原式
例 求 的值.
解:
原式
例 求 的值.
解:
原式
例 求 的值.
解:
原式
例 求 的值.
例 化简
分析:
例 化简
分析:
例 化简
分析:
例 化简
分析:
例 化简
分析:
例 化简
解:
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
例 设 ,将 用含 的式子表示
分析:
例 设 ,将 用含 的式子表示
分析:
例 设 ,将 用含 的式子表示
分析:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
令 ,
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
求 的值.
例 已知 ,且
解:
求 的值.
例 已知 ,且
解:
令 ,
求 的值.
例 已知 ,且
解:
令 ,
则 ,
求 的值.
例 已知 ,且
解:
令 ,
则 ,
求 的值.
例 已知 ,且
解:
令 ,
则 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
因为
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
因为
所以 .
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
因为
所以 .
所以
所以
求 的值.
例 已知 ,且
求 的值.
解:
例 已知 ,且
令 ,
则 ,
因为 ,
所以 .
因为
所以 .
所以
所以
求 的值.
解:
例 已知 ,且
求 的值.
解:
例 已知 ,且
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
求 的值.
解:
例 已知 ,且
因为
求 的值.
解:
例 已知 ,且
因为
所以
求 的值.
解:
例 已知 ,且
因为
所以
因为
求 的值.
解:
例 已知 ,且
因为
所以
因为
所以
求 的值.
解:
例 已知 ,且
因为
所以
因为
所以
求 的值.
解:
例 已知 ,且
因为
所以
因为
所以
例 求
分析:
例 求
分析:
例 求
分析:
例 求
分析:
例 求
分析:
例 求
分析:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
原式
例 求
小结
小结
1.
角的关系 → 三角函数值的关系.
小结
1.
角的关系 → 三角函数值的关系.
2.
确定合适的变形方向,
运用相应的诱导公式,
实现角度的统一.
小结
1.
角的关系 → 三角函数值的关系.
2.
确定合适的变形方向,
运用相应的诱导公式,
实现角度的统一.
3.
注意角的范围和同角三角函数
关系式的应用
基础性作业
1. 已知 ,分别求下列各式的值
(1)
(2)
2. 化简
发展性作业
1. 若 ,则 与 有什么关系?
2. 若 ,则 与 有什么关系?
感谢聆听
高一年级 数学
诱导公式应用
复习
1. 在前两节课中,我们学到了哪些诱导公式 ?
复习
1. 在前两节课中,我们学到了哪些诱导公式 ?
2. 它们是如何得到的 ?
复习
1. 在前两节课中,我们学到了哪些诱导公式 ?
2. 它们是如何得到的 ?
3. 如何利用这些公式求值、化简、证明?
复习
复习
复习
复习
其中
复习
其中
复习
其中
复习
其中
复习
复习
复习
负化正,
利用对称凑锐角.
大化小.
任意负角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
角的
三角函数
任意负角的
三角函数
任意正角的
三角函数
角的
三角函数
角的
三角函数
复习
负化正,
利用对称凑锐角.
大化小.
复习
负化正,
利用对称凑锐角.
大化小.
角的关系 → 三角函数值的关系
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
例 求 的值.
解:
原式
例 求 的值.
解:
原式
例 求 的值.
解:
原式
例 求 的值.
解:
原式
例 求 的值.
例 化简
分析:
例 化简
分析:
例 化简
分析:
例 化简
分析:
例 化简
分析:
例 化简
解:
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
解:
原式
例 化简
例 设 ,将 用含 的式子表示
分析:
例 设 ,将 用含 的式子表示
分析:
例 设 ,将 用含 的式子表示
分析:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
解:
例 设 ,将 用含 的式子表示
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
和为
差为
和为
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
解:
例 已知 ,且 .
求 , 的值.
令 ,
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
解:
例 已知 ,且 .
求 , 的值.
令 ,
则
求 的值.
例 已知 ,且
解:
求 的值.
例 已知 ,且
解:
令 ,
求 的值.
例 已知 ,且
解:
令 ,
则 ,
求 的值.
例 已知 ,且
解:
令 ,
则 ,
求 的值.
例 已知 ,且
解:
令 ,
则 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
因为
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
因为
所以 .
所以
求 的值.
例 已知 ,且
解:
令 ,
则 ,
因为 ,
所以 .
因为
所以 .
所以
所以
求 的值.
例 已知 ,且
求 的值.
解:
例 已知 ,且
令 ,
则 ,
因为 ,
所以 .
因为
所以 .
所以
所以
求 的值.
解:
例 已知 ,且
求 的值.
解:
例 已知 ,且
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
和为
求 的值.
解:
例 已知 ,且
求 的值.
解:
例 已知 ,且
因为
求 的值.
解:
例 已知 ,且
因为
所以
求 的值.
解:
例 已知 ,且
因为
所以
因为
求 的值.
解:
例 已知 ,且
因为
所以
因为
所以
求 的值.
解:
例 已知 ,且
因为
所以
因为
所以
求 的值.
解:
例 已知 ,且
因为
所以
因为
所以
例 求
分析:
例 求
分析:
例 求
分析:
例 求
分析:
例 求
分析:
例 求
分析:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
例 求
解:
原式
例 求
小结
小结
1.
角的关系 → 三角函数值的关系.
小结
1.
角的关系 → 三角函数值的关系.
2.
确定合适的变形方向,
运用相应的诱导公式,
实现角度的统一.
小结
1.
角的关系 → 三角函数值的关系.
2.
确定合适的变形方向,
运用相应的诱导公式,
实现角度的统一.
3.
注意角的范围和同角三角函数
关系式的应用
基础性作业
1. 已知 ,分别求下列各式的值
(1)
(2)
2. 化简
发展性作业
1. 若 ,则 与 有什么关系?
2. 若 ,则 与 有什么关系?
感谢聆听
