五年级下册数学课件-6.3 总复习:式与方程 ▏沪教版 (共30张PPT)
文档属性
| 名称 | 五年级下册数学课件-6.3 总复习:式与方程 ▏沪教版 (共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览










文档简介
(共30张PPT)
数与代数
式与方程
整理和复习
复习目标
1、进一步认识用字母表示及其作用,能正确的用含有
字母的式子表示数量及数量关系。
2、掌握解方程的方法及列方程解决问题的步骤;知道
解决问题的关键是找出数量之间的相等关系;能根
据题意正确的列出方程解答两、三步计算的问题。
3、根据问题的特点选择恰当的方法来解答,进一步培
养学生分析数量关系的能力,发散学生的思维。
4、培养学生抽象、概括的能力和检查、验算的习惯。
探索知识间的内在联系,激发学生的学习兴趣。
知识梳理
2、你知道哪些用字母表示的数量关系、运算定律和公式?
3、在含有字母的式子里,数和字母、字母和字母相乘,
书写时应注意什么?
4、什么叫做方程?什么叫做解方程?什么叫做方程的解?
小组或同桌讨论、回顾式与方程的知识,回答下列问题。
1、用字母表示数有什么意义或作用?
5、方程和等式有什么联系和区别?
6、什么是等式的性质?你能举例说明等式的性质吗?
8、用方程解决实际问题有什么特点?解题步骤是什么?
7、如何解方程?解方程的依据是什么?
1、字母表示数有什么意义和作用?
数量、数量关系可以用含有字母的式子简明概括的表达出来。用字母还可以表示运算定律和常见的计算公式等。
知识梳理
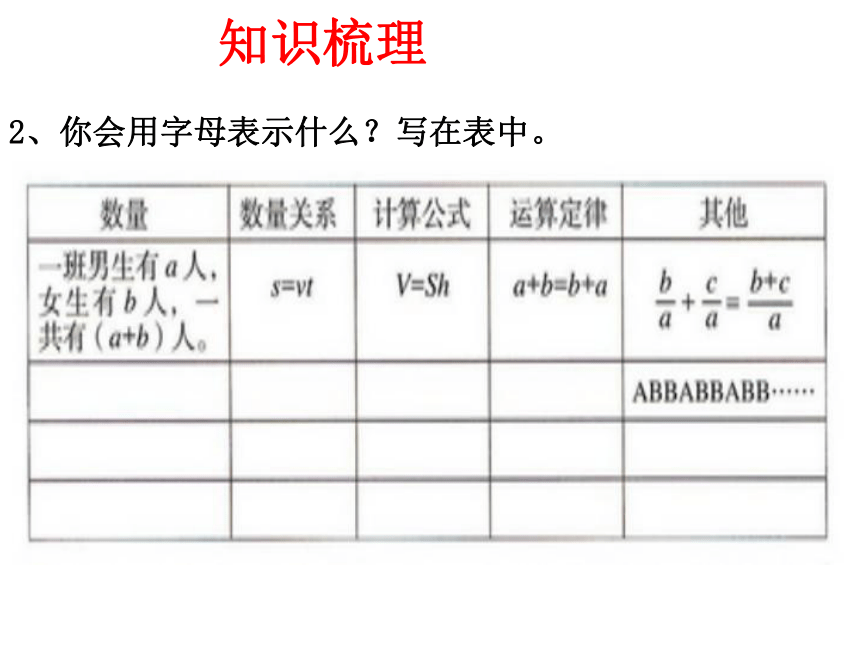
2、你会用字母表示什么?写在表中。
知识梳理
你知道哪些用字母表示的公式:
长方形面积公式:
正方形面积公式:
长方体体积公式:
正方体体积公式:
圆周长公式:
圆面积公式:
圆柱体积公式:
圆锥体积公式:
s=ab
s=a?
v=abh
v=a?
c=2πr
s=πr?
v=sh
v=
3
_
1
sh
知识梳理
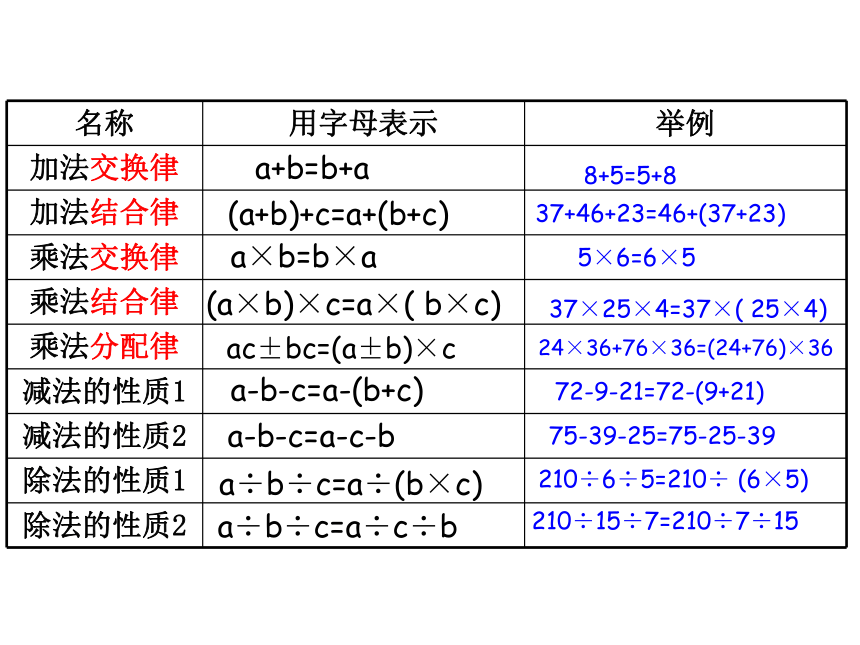
运算定律和运算性质:
名称 用字母表示 举例
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法的性质1
减法的性质2
除法的性质1
除法的性质2
a×b=b×a
(a×b)×c=a×( b×c)
ac±bc=(a±b)×c
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
a-b-c=a-c-b
a÷b÷c=a÷(b×c)
a÷b÷c=a÷c÷b
5×6=6×5
37×25×4=37×( 25×4)
24×36+76×36=(24+76)×36
8+5=5+8
37+46+23=46+(37+23)
72-9-21=72-(9+21)
75-39-25=75-25-39
210÷6÷5=210÷ (6×5)
210÷15÷7=210÷7÷15
知识梳理
①含有字母的式子里,数和字母中间的乘号可以记作
“·”,也可以省略不写。
②省略乘号时,应该把数写在字母的前面。
③数与数之间的乘号不能省略。
加号、减号、除号都不能省略。
如:6×a=6·a=6a
3、在一个含有字母的式子里,数与字母,字母与
字母相乘,书写时应该注意什么?
知识梳理
4、什么叫做方程?什么叫做解方程?什么叫做方程的解?
①含有未知数的等式叫做方程。
未知数
等式
方程的两要素
②解方程:求方程的解的过程,叫做解方程。
③方程的解: 使方程左右两边相等的未知数的值。
那什么是等式呢?
表示两个数或两个代数式相等关系的式子叫做等式。
5、方程与等式有什么区别与联系?
方程 等式
等式 方程。
一定是
不一定是
知识梳理
哪些是方程?
1.9+7=8.9 3x+6>9 2.5x-1.5=1
x+ <12 x+10=36x 3+11≠12
性质1:等式两边同时加上(或减去)同一个数,等式仍然成立。
性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立。
性质3:等式具有传递性。
那么
若 ,那么
若 ,那么 或
若 , , ,……
知识梳理
6、什么是等式的性质?你能举例说明等式的性质吗?
知识梳理
7、如何解方程?解方程的依据是什么?
可以根据等式的基本性质和比例的基本性质来解方程。
8、用方程解决实际问题有什么特点?解题步骤是什么?
知识梳理
阅读与理解题意
根据题意设未知数
找出数量关系
根据数量关系列方程
解方程、作答
回顾检查
1、连线。
比a多3的数
比a少3的数
3个a相加的和
a的3倍
a的
3
1
3a
a+3
a-3
练习、讲评
3个a相乘的积
小平在踢毽子比赛中踢了42下,她踢的数量是小云的 ,小云踢了多少下?(用方程解决问题)
等量关系:小平踢毽子数=小云踢毽子数×
解:设小云踢了x下
答:小云踢了56下。
练习、讲评
1、学校买来9个足球,每个a元,又买来b个篮球,每 个58元。
9a表示
58b表示
9个足球多少元
b个篮球多少元
一个篮球比一个足球贵多少元
买9个足球, b个篮球一共需要多少元
表示
表示
如果a=45,b=6,则9a+58b=
2778
练习、讲评
2、(1)工地上有a吨水泥,如果每天用去2.5吨,用了b天,剩下的吨数为( )
(2)已知
,剩下的吨数为 ( )
75吨
3、小丽家的草莓去年收获500千克,今年比去年增产两成,今年收获 ( )千克。
600
练习、讲评
4、用小棒摆正方形
正方形个数 图形 小棒的根数
1 4
2
3
…… …… ……
(1)你发现了什么规律?
(2)如果摆n个正方形需要( )根小棒。
摆150个正方形,需要( )根小棒。
每增加一个正方形,需要多3根小棒。
451
练习、讲评
5、解方程。
(1)
(4)
(3)
(2)
解:
解:
解:
解:
练习、讲评
6、三个连续的自然数,中间的数是a,则a前面和后面分别是( )、( )。
7、当n表示所有的自然数0,1,2,3,4,5……时,2n表示什么数? 呢?
2n表示所有的偶数
表示所有的奇数
练习、讲评
8、一台电视机打八五折后售价为2975元,这台电视机原价多少元钱?
解:设这台电视机原价x元。
答:这台电视机原价3500元。
练习、讲评
原价×八五折=现价
9、绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵树的2倍。栽了多少棵丁香花?
解:设栽了x棵丁香花。
答:栽了128棵丁香花。
练习、讲评
月季花数量+16棵=丁香花数量×2
10、阳阳在读一本科普书,第一周读了90页,还剩下这本书的 没读。这本科普书一共有多少页?
解:设这本科普书一共有x页。
答:这本科普书一共有135页。
练习、讲评
总页数-总页数× =第一周读页数
11、湖北丹江口水库与2014年向北京、天津、河南、河北等地供水。蓄水量将达290亿立方米,比北京密云水库蓄水量的26倍还多4亿立方米。密云水库蓄水量是多少?
答:密云水库蓄水量是11立方米。
练习、讲评
丹江口水库水量=密云水库水量×26倍+4亿立方米
解:设密云水库需水量是x亿立方米。
12、商店卖一种书包,如果每个售价为150元,那么售价的60%是进价,售价的40%就是赚的钱。现在要搞促销活动,为保证一个书包赚的钱不少于30元,应该怎样确定折扣?
解:设折扣是x。
答:要保证一个书包赚的钱不少于30元,折扣不少于5折。
练习、讲评
售价 x折扣 ×40%=赚的钱
13、小明家住在电影院的正西650米,小冬家住在电影院的正东700米。周末两人约好去看下午3时放映的电影。两人下午2点45分同时从家里出发走向电影院。小明每分钟步行70米,小冬每分钟步行65米。
(1)2点55分两人能在电影院相遇吗?
(2)如果小明先到电影院后不停留继续向东走,从出发到相遇用了多长时间?相遇地点距离电影院有多远?
从2点45分到2点55分有10分钟。
练习、讲评
小明:
小冬:
(1)10分钟后两人走的路程
答:这个时候小冬还没有到达电影院,所以他们不能在电影院相遇。
解:设从出发到相遇用了x分钟。
(米)
答:从出发到相遇用了10分钟,相遇地点距离电影院有50米。
练习、讲评
700米>650米
速度×相遇时间=总路程
(2)、
14、一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只。如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
解:设蜘蛛是x只,蚱蜢(25- x)只
答:蜘蛛有10只,蚱蜢有15只。
练习、讲评
蜘蛛数量+蚱蜢数量=25只总数量
蜘蛛数量×8+蚱蜢数量×6=170条腿
蚱蜢:25-10=15(只)
1、掌握用字母表示数和常见的数量关系。
2、认识等式与方程的联系。
3、在实际应用题中会根据题意找等量关系并列出方程式。
4、会解简单的方程。
回顾小结
同学们,关于“式与方程”的知识点你们还知道了哪些?和同桌或小组交流,温故知新哦!
数与代数
式与方程
整理和复习
复习目标
1、进一步认识用字母表示及其作用,能正确的用含有
字母的式子表示数量及数量关系。
2、掌握解方程的方法及列方程解决问题的步骤;知道
解决问题的关键是找出数量之间的相等关系;能根
据题意正确的列出方程解答两、三步计算的问题。
3、根据问题的特点选择恰当的方法来解答,进一步培
养学生分析数量关系的能力,发散学生的思维。
4、培养学生抽象、概括的能力和检查、验算的习惯。
探索知识间的内在联系,激发学生的学习兴趣。
知识梳理
2、你知道哪些用字母表示的数量关系、运算定律和公式?
3、在含有字母的式子里,数和字母、字母和字母相乘,
书写时应注意什么?
4、什么叫做方程?什么叫做解方程?什么叫做方程的解?
小组或同桌讨论、回顾式与方程的知识,回答下列问题。
1、用字母表示数有什么意义或作用?
5、方程和等式有什么联系和区别?
6、什么是等式的性质?你能举例说明等式的性质吗?
8、用方程解决实际问题有什么特点?解题步骤是什么?
7、如何解方程?解方程的依据是什么?
1、字母表示数有什么意义和作用?
数量、数量关系可以用含有字母的式子简明概括的表达出来。用字母还可以表示运算定律和常见的计算公式等。
知识梳理
2、你会用字母表示什么?写在表中。
知识梳理
你知道哪些用字母表示的公式:
长方形面积公式:
正方形面积公式:
长方体体积公式:
正方体体积公式:
圆周长公式:
圆面积公式:
圆柱体积公式:
圆锥体积公式:
s=ab
s=a?
v=abh
v=a?
c=2πr
s=πr?
v=sh
v=
3
_
1
sh
知识梳理
运算定律和运算性质:
名称 用字母表示 举例
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
减法的性质1
减法的性质2
除法的性质1
除法的性质2
a×b=b×a
(a×b)×c=a×( b×c)
ac±bc=(a±b)×c
a+b=b+a
(a+b)+c=a+(b+c)
a-b-c=a-(b+c)
a-b-c=a-c-b
a÷b÷c=a÷(b×c)
a÷b÷c=a÷c÷b
5×6=6×5
37×25×4=37×( 25×4)
24×36+76×36=(24+76)×36
8+5=5+8
37+46+23=46+(37+23)
72-9-21=72-(9+21)
75-39-25=75-25-39
210÷6÷5=210÷ (6×5)
210÷15÷7=210÷7÷15
知识梳理
①含有字母的式子里,数和字母中间的乘号可以记作
“·”,也可以省略不写。
②省略乘号时,应该把数写在字母的前面。
③数与数之间的乘号不能省略。
加号、减号、除号都不能省略。
如:6×a=6·a=6a
3、在一个含有字母的式子里,数与字母,字母与
字母相乘,书写时应该注意什么?
知识梳理
4、什么叫做方程?什么叫做解方程?什么叫做方程的解?
①含有未知数的等式叫做方程。
未知数
等式
方程的两要素
②解方程:求方程的解的过程,叫做解方程。
③方程的解: 使方程左右两边相等的未知数的值。
那什么是等式呢?
表示两个数或两个代数式相等关系的式子叫做等式。
5、方程与等式有什么区别与联系?
方程 等式
等式 方程。
一定是
不一定是
知识梳理
哪些是方程?
1.9+7=8.9 3x+6>9 2.5x-1.5=1
x+ <12 x+10=36x 3+11≠12
性质1:等式两边同时加上(或减去)同一个数,等式仍然成立。
性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立。
性质3:等式具有传递性。
那么
若 ,那么
若 ,那么 或
若 , , ,……
知识梳理
6、什么是等式的性质?你能举例说明等式的性质吗?
知识梳理
7、如何解方程?解方程的依据是什么?
可以根据等式的基本性质和比例的基本性质来解方程。
8、用方程解决实际问题有什么特点?解题步骤是什么?
知识梳理
阅读与理解题意
根据题意设未知数
找出数量关系
根据数量关系列方程
解方程、作答
回顾检查
1、连线。
比a多3的数
比a少3的数
3个a相加的和
a的3倍
a的
3
1
3a
a+3
a-3
练习、讲评
3个a相乘的积
小平在踢毽子比赛中踢了42下,她踢的数量是小云的 ,小云踢了多少下?(用方程解决问题)
等量关系:小平踢毽子数=小云踢毽子数×
解:设小云踢了x下
答:小云踢了56下。
练习、讲评
1、学校买来9个足球,每个a元,又买来b个篮球,每 个58元。
9a表示
58b表示
9个足球多少元
b个篮球多少元
一个篮球比一个足球贵多少元
买9个足球, b个篮球一共需要多少元
表示
表示
如果a=45,b=6,则9a+58b=
2778
练习、讲评
2、(1)工地上有a吨水泥,如果每天用去2.5吨,用了b天,剩下的吨数为( )
(2)已知
,剩下的吨数为 ( )
75吨
3、小丽家的草莓去年收获500千克,今年比去年增产两成,今年收获 ( )千克。
600
练习、讲评
4、用小棒摆正方形
正方形个数 图形 小棒的根数
1 4
2
3
…… …… ……
(1)你发现了什么规律?
(2)如果摆n个正方形需要( )根小棒。
摆150个正方形,需要( )根小棒。
每增加一个正方形,需要多3根小棒。
451
练习、讲评
5、解方程。
(1)
(4)
(3)
(2)
解:
解:
解:
解:
练习、讲评
6、三个连续的自然数,中间的数是a,则a前面和后面分别是( )、( )。
7、当n表示所有的自然数0,1,2,3,4,5……时,2n表示什么数? 呢?
2n表示所有的偶数
表示所有的奇数
练习、讲评
8、一台电视机打八五折后售价为2975元,这台电视机原价多少元钱?
解:设这台电视机原价x元。
答:这台电视机原价3500元。
练习、讲评
原价×八五折=现价
9、绿化队为一个居民社区栽花。栽月季花240棵,再加上16棵就是所栽丁香花棵树的2倍。栽了多少棵丁香花?
解:设栽了x棵丁香花。
答:栽了128棵丁香花。
练习、讲评
月季花数量+16棵=丁香花数量×2
10、阳阳在读一本科普书,第一周读了90页,还剩下这本书的 没读。这本科普书一共有多少页?
解:设这本科普书一共有x页。
答:这本科普书一共有135页。
练习、讲评
总页数-总页数× =第一周读页数
11、湖北丹江口水库与2014年向北京、天津、河南、河北等地供水。蓄水量将达290亿立方米,比北京密云水库蓄水量的26倍还多4亿立方米。密云水库蓄水量是多少?
答:密云水库蓄水量是11立方米。
练习、讲评
丹江口水库水量=密云水库水量×26倍+4亿立方米
解:设密云水库需水量是x亿立方米。
12、商店卖一种书包,如果每个售价为150元,那么售价的60%是进价,售价的40%就是赚的钱。现在要搞促销活动,为保证一个书包赚的钱不少于30元,应该怎样确定折扣?
解:设折扣是x。
答:要保证一个书包赚的钱不少于30元,折扣不少于5折。
练习、讲评
售价 x折扣 ×40%=赚的钱
13、小明家住在电影院的正西650米,小冬家住在电影院的正东700米。周末两人约好去看下午3时放映的电影。两人下午2点45分同时从家里出发走向电影院。小明每分钟步行70米,小冬每分钟步行65米。
(1)2点55分两人能在电影院相遇吗?
(2)如果小明先到电影院后不停留继续向东走,从出发到相遇用了多长时间?相遇地点距离电影院有多远?
从2点45分到2点55分有10分钟。
练习、讲评
小明:
小冬:
(1)10分钟后两人走的路程
答:这个时候小冬还没有到达电影院,所以他们不能在电影院相遇。
解:设从出发到相遇用了x分钟。
(米)
答:从出发到相遇用了10分钟,相遇地点距离电影院有50米。
练习、讲评
700米>650米
速度×相遇时间=总路程
(2)、
14、一个笼子里有8条腿的蜘蛛和6条腿的蚱蜢共25只。如果它们的总腿数有170条,那么蜘蛛和蚱蜢各有多少只?
解:设蜘蛛是x只,蚱蜢(25- x)只
答:蜘蛛有10只,蚱蜢有15只。
练习、讲评
蜘蛛数量+蚱蜢数量=25只总数量
蜘蛛数量×8+蚱蜢数量×6=170条腿
蚱蜢:25-10=15(只)
1、掌握用字母表示数和常见的数量关系。
2、认识等式与方程的联系。
3、在实际应用题中会根据题意找等量关系并列出方程式。
4、会解简单的方程。
回顾小结
同学们,关于“式与方程”的知识点你们还知道了哪些?和同桌或小组交流,温故知新哦!
