人教数学六年级下册第3单元 圆柱与圆锥3.2 圆柱的表面积 课件(25张ppt)
文档属性
| 名称 | 人教数学六年级下册第3单元 圆柱与圆锥3.2 圆柱的表面积 课件(25张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
3.2 圆柱的表面积
1. 理解圆柱的侧面积和表面积的含义,掌握圆柱的侧面积的计算方法,会正确计算圆柱的侧面积。(重点)
2. 能正确地计算圆柱的表面积。(重点)
3. 能运用求圆柱的侧面积、表面积的相关知识,解决生活中的实际问题。(难点)
一个圆形花池,直径是3 m,周长是多少米?
3.14×3=9.42(米)
答:周长是9.42米。
知识点1
圆柱的表面积和侧面积的意义及计算公式
3
圆柱的表面积指的是什么?
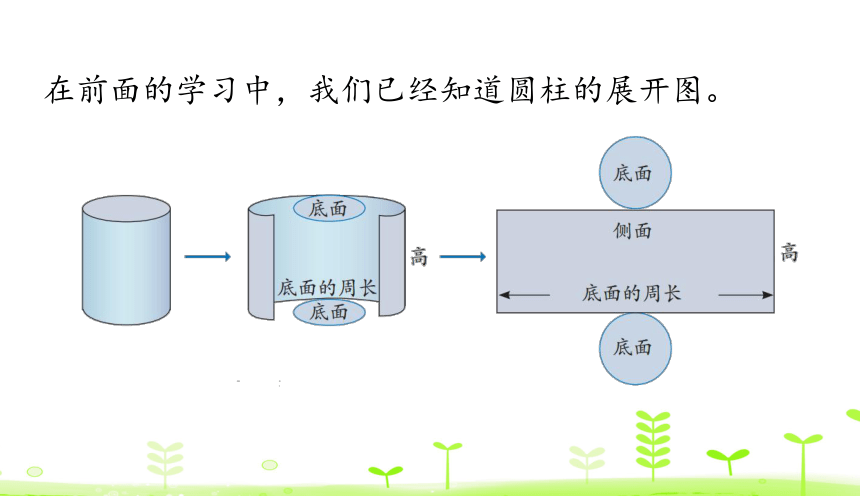
在前面的学习中,我们已经知道圆柱的展开图。
底面
底面
高
底面的周长
底面
底面
底面的周长
高
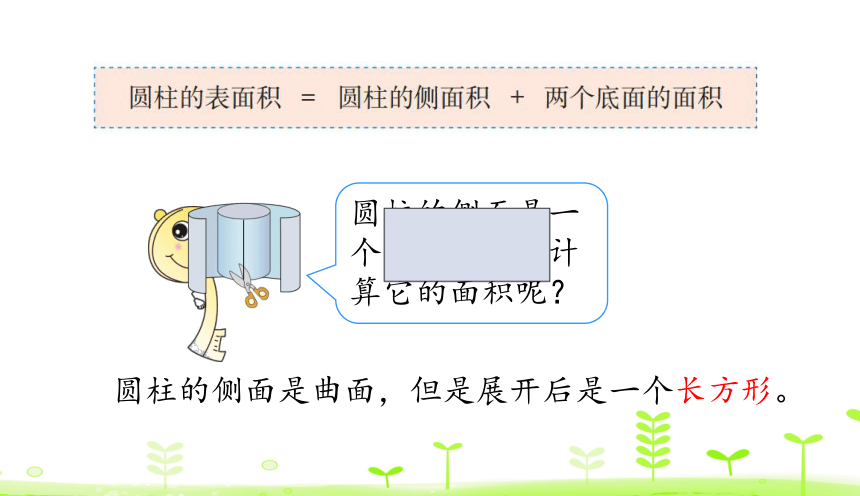
圆柱的表面积指的是圆柱侧面积与两个底面积的和。
圆柱的侧面是一个曲面,怎样计算它的面积呢?
圆柱的侧面是曲面,但是展开后是一个长方形。
高
底面的周长
侧面
底面的周长
高
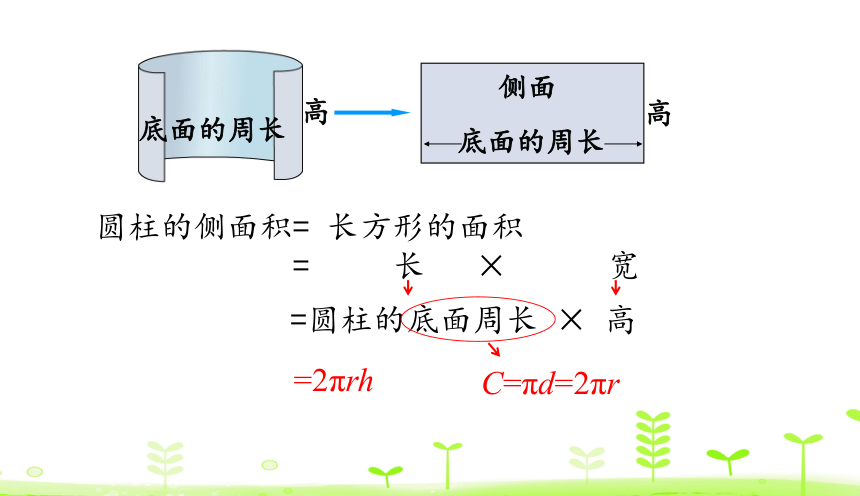
圆柱的侧面积= 长方形的面积
= 长 × 宽
=圆柱的底面周长 × 高
C=πd=2πr
=2πrh
知识点2
圆柱表面积计算公式的实际应用
4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
帽子的表面积=帽子的侧面积+帽顶面积
(1)帽子的侧面积:3.14×20×30=1884(cm2 )
(2)帽顶的面积:3.14×(20÷2)2=314(cm2 )
(3)需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200平方厘米的面料。
实际使用的面料要比计算的结果多一些,
所以这类问题往往用“进一法”取近似数。
1.圆柱的侧面积=底面周长×高。
用字母表示是S侧=Ch=πdh=2πrh。
知识提炼
c
2π
( )2
d
2
( )2
2.圆柱的表面积=圆柱的侧面积+两个底面的面积,用字母表示是S表=S侧+2S底=2πrh+2πr =πdh+2π
=Ch+2π
小试牛刀
一个圆柱形茶叶桶的侧面贴着商标纸,圆柱底面半
径是5cm,高是20cm。这张商标纸的面积是多少?
(选自教材P21做一做)
答:这张商标纸的面积是628 平方厘米。
2×3.14×5×20=628(cm2)
求下面各圆柱的侧面积。(选自教材P22做一做)
(1)底面周长是1.6m,高是0.7m。
1.6×0.7=1.12(m2)
答:圆柱的侧面积是1.12 平方米。
(2)底面半径是3.2dm,高5dm。
2×3.14×3.2×5=100.48(dm2 )
答:圆柱的侧面积是100.48 平方分米。
1.求下面各圆柱的表面积(图中长度单位: cm)。
3.14×6×12+3.14× ×2=282.6(cm )
6
2
( )2
(选自教材P23 T1)
求下面各圆柱的表面积(图中长度单位: cm)。
3.14×40×3+3.14× ×2=282.6(cm )
( )2
40
2
求下面各圆柱的表面积(图中长度单位: cm)。
3.14×18×15+3.14× ×2=1356.48(cm )
( )2
18
2
2.广告公司制作了一个底面直径是 1.5 m、高 2.5 m 的圆柱形灯箱。可以张贴多大面积的海报?
3.14×1.5×2.5=11.775(m )
答:可以张贴11.775 平方米的海报。
(选自教材P23 T3)
3.填空题。
(1)用一张长5cm、宽8cm的长方形纸围成一个圆柱,这个圆柱的侧面积是( )。
(2)一个圆柱的侧面积是12.56平方厘米,底面积是3.14平方厘米,它的表面积是( )。
40cm
18.84cm
4.做一个无盖的圆柱形玻璃杯,底面直径和高都是6cm,它的表面积是多少平方厘米?
(6÷2) ×3.14+6×3.14×6=141.3(cm )
答:它的表面积是141.3平方厘米。
5.如图所示是一个圆柱形队鼓,队鼓的侧面由铝皮围成,上、下底面蒙的羊皮。做一个这样的队鼓,至少需要铝皮多少平方分米?至少需要羊皮多少平方分米?(得数取整数)
铝皮:6×3.14×2.6≈49(dm )
羊皮:(6÷2) ×3.14×2≈57(dm )
答:至少需要铝皮49平方分米,至少需要羊皮57平方分米。
6.小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?(选自教材P22做一做)
8cm
13cm
表面积
笔筒的侧面积+笔筒的一个底面积
侧面:3.14×8×13=326.56(cm2)
底面:3.14×(8÷2)2=50.24(cm2)
侧面积:326.56+50.24=376.8(cm2)
答:至少需要 376.8 平方厘米彩纸。
1.圆柱的侧面积=底面周长×高。
用字母表示是S侧=Ch=πdh=2πrh。
c
2π
( )2
d
2
( )2
2.圆柱的表面积=圆柱的侧面积+两个底面的面积,用字母表示是S表=S侧+2S底=2πrh+2πr =πdh+2π
=Ch+2π
作业1:预习下一课。
作业2:完成教材详解对应的练习题。
3.2 圆柱的表面积
1. 理解圆柱的侧面积和表面积的含义,掌握圆柱的侧面积的计算方法,会正确计算圆柱的侧面积。(重点)
2. 能正确地计算圆柱的表面积。(重点)
3. 能运用求圆柱的侧面积、表面积的相关知识,解决生活中的实际问题。(难点)
一个圆形花池,直径是3 m,周长是多少米?
3.14×3=9.42(米)
答:周长是9.42米。
知识点1
圆柱的表面积和侧面积的意义及计算公式
3
圆柱的表面积指的是什么?
在前面的学习中,我们已经知道圆柱的展开图。
底面
底面
高
底面的周长
底面
底面
底面的周长
高
圆柱的表面积指的是圆柱侧面积与两个底面积的和。
圆柱的侧面是一个曲面,怎样计算它的面积呢?
圆柱的侧面是曲面,但是展开后是一个长方形。
高
底面的周长
侧面
底面的周长
高
圆柱的侧面积= 长方形的面积
= 长 × 宽
=圆柱的底面周长 × 高
C=πd=2πr
=2πrh
知识点2
圆柱表面积计算公式的实际应用
4
一顶圆柱形厨师帽,高30cm,帽顶直径20cm,做这样一顶帽子至少要用多少平方厘米的面料?(得数保留整十数。)
帽子的表面积=帽子的侧面积+帽顶面积
(1)帽子的侧面积:3.14×20×30=1884(cm2 )
(2)帽顶的面积:3.14×(20÷2)2=314(cm2 )
(3)需要用的面料:1884+314=2198≈2200(cm2 )
答:做这样一顶帽子至少要用2200平方厘米的面料。
实际使用的面料要比计算的结果多一些,
所以这类问题往往用“进一法”取近似数。
1.圆柱的侧面积=底面周长×高。
用字母表示是S侧=Ch=πdh=2πrh。
知识提炼
c
2π
( )2
d
2
( )2
2.圆柱的表面积=圆柱的侧面积+两个底面的面积,用字母表示是S表=S侧+2S底=2πrh+2πr =πdh+2π
=Ch+2π
小试牛刀
一个圆柱形茶叶桶的侧面贴着商标纸,圆柱底面半
径是5cm,高是20cm。这张商标纸的面积是多少?
(选自教材P21做一做)
答:这张商标纸的面积是628 平方厘米。
2×3.14×5×20=628(cm2)
求下面各圆柱的侧面积。(选自教材P22做一做)
(1)底面周长是1.6m,高是0.7m。
1.6×0.7=1.12(m2)
答:圆柱的侧面积是1.12 平方米。
(2)底面半径是3.2dm,高5dm。
2×3.14×3.2×5=100.48(dm2 )
答:圆柱的侧面积是100.48 平方分米。
1.求下面各圆柱的表面积(图中长度单位: cm)。
3.14×6×12+3.14× ×2=282.6(cm )
6
2
( )2
(选自教材P23 T1)
求下面各圆柱的表面积(图中长度单位: cm)。
3.14×40×3+3.14× ×2=282.6(cm )
( )2
40
2
求下面各圆柱的表面积(图中长度单位: cm)。
3.14×18×15+3.14× ×2=1356.48(cm )
( )2
18
2
2.广告公司制作了一个底面直径是 1.5 m、高 2.5 m 的圆柱形灯箱。可以张贴多大面积的海报?
3.14×1.5×2.5=11.775(m )
答:可以张贴11.775 平方米的海报。
(选自教材P23 T3)
3.填空题。
(1)用一张长5cm、宽8cm的长方形纸围成一个圆柱,这个圆柱的侧面积是( )。
(2)一个圆柱的侧面积是12.56平方厘米,底面积是3.14平方厘米,它的表面积是( )。
40cm
18.84cm
4.做一个无盖的圆柱形玻璃杯,底面直径和高都是6cm,它的表面积是多少平方厘米?
(6÷2) ×3.14+6×3.14×6=141.3(cm )
答:它的表面积是141.3平方厘米。
5.如图所示是一个圆柱形队鼓,队鼓的侧面由铝皮围成,上、下底面蒙的羊皮。做一个这样的队鼓,至少需要铝皮多少平方分米?至少需要羊皮多少平方分米?(得数取整数)
铝皮:6×3.14×2.6≈49(dm )
羊皮:(6÷2) ×3.14×2≈57(dm )
答:至少需要铝皮49平方分米,至少需要羊皮57平方分米。
6.小亚做了一个笔筒,她想给笔筒的侧面和底面贴上彩纸,至少需要用多少彩纸?(选自教材P22做一做)
8cm
13cm
表面积
笔筒的侧面积+笔筒的一个底面积
侧面:3.14×8×13=326.56(cm2)
底面:3.14×(8÷2)2=50.24(cm2)
侧面积:326.56+50.24=376.8(cm2)
答:至少需要 376.8 平方厘米彩纸。
1.圆柱的侧面积=底面周长×高。
用字母表示是S侧=Ch=πdh=2πrh。
c
2π
( )2
d
2
( )2
2.圆柱的表面积=圆柱的侧面积+两个底面的面积,用字母表示是S表=S侧+2S底=2πrh+2πr =πdh+2π
=Ch+2π
作业1:预习下一课。
作业2:完成教材详解对应的练习题。
