人教数学六年级下册第3单元第3单元 圆柱与圆锥3.3 圆柱的体积 课件(24张ppt)
文档属性
| 名称 | 人教数学六年级下册第3单元第3单元 圆柱与圆锥3.3 圆柱的体积 课件(24张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览





文档简介
(共24张PPT)
3.3 圆柱的体积
1. 探索圆柱的体积计算公式,会运用公式计算圆柱的体积。(重点)
2. 能运用圆柱体积计算公式解决实际问题,体会转化思想的实际应用。(难点)
怎样求圆的面积 圆的面积公式是什么
圆的面积=圆周率×半径的平方
字母公式:S = πr
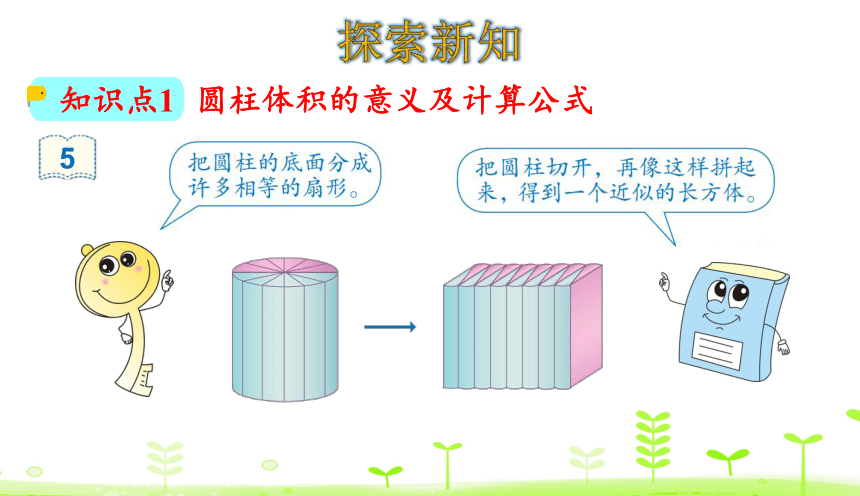
知识点1
圆柱体积的意义及计算公式
5
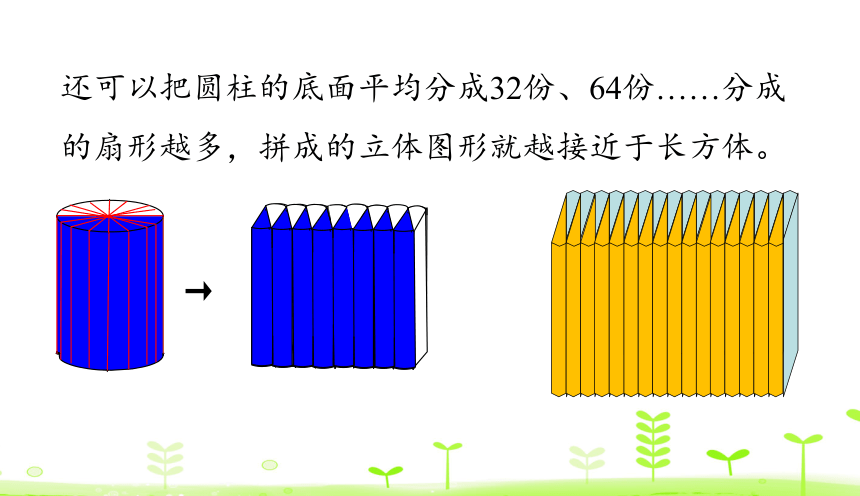
还可以把圆柱的底面平均分成32份、64份……分成的扇形越多,拼成的立体图形就越接近于长方体。
→
比较拼成的长方体与原来的圆柱,可以发现长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
→
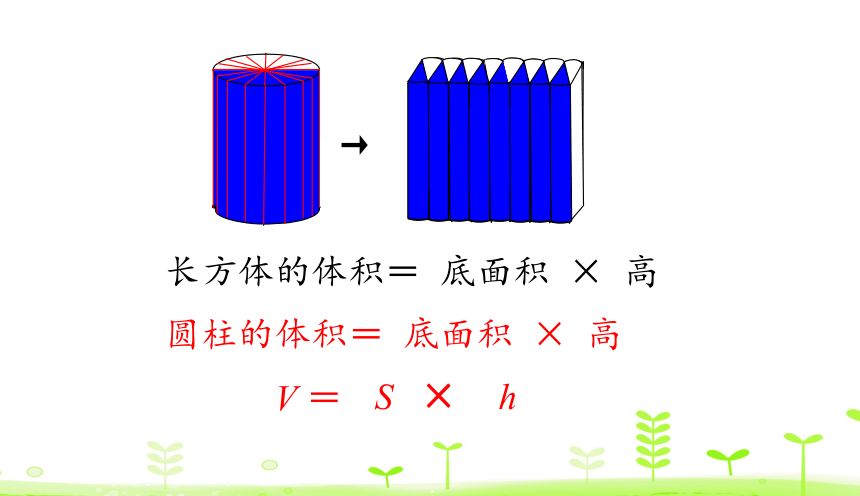
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V =
S ×
h
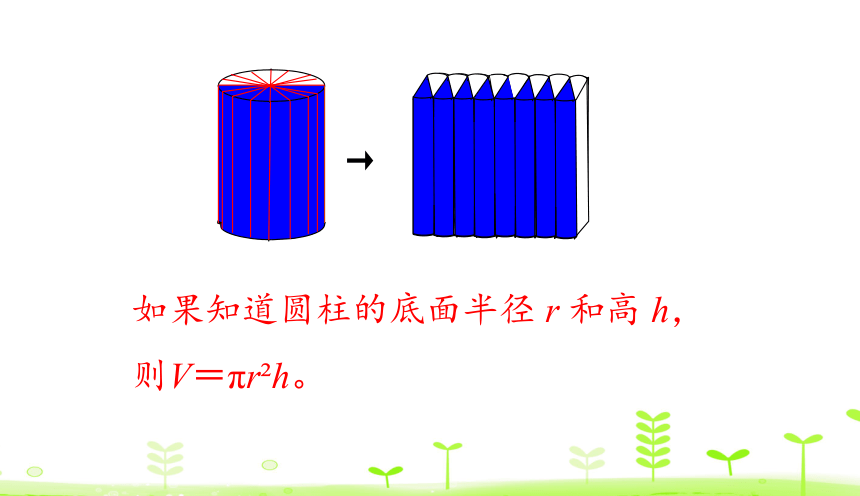
如果知道圆柱的底面半径 r 和高 h,
则V=πr h。
→
圆柱的体积=底面积×高,用字母表示是 V=Sh,圆柱的底面积=πr ,所以 V=πr h。
知识提炼
小试牛刀
一根圆柱形木料,底面积为75cm ,长90cm。它的
体积是多少?(选自教材P25做一做T1)
75×90=6750(cm )
答:它的体积是6750 立方厘米。
知识点2
圆柱体积计算公式的实际应用
6
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
容积的计算方法与体积的计算方法相同。
杯子的底面积:
3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24 (cm2 )
杯子的容积:
50.24×10
=502.4 (cm3 )
=502.4 (mL)
答:因为502.4 大于498,所以杯子能装下这袋牛奶。
容积是容器所能容纳物体的体积,圆柱形容器的容积求法和圆柱体积的求法是一样的,只是所需的数据要从容器的里面量。
知识提炼
小明和妈妈出去游玩,带了一个圆柱形保温杯,
从里面量底面直径是8cm,高是15cm。如果两
人游玩期间要喝 1L水,带这杯水够喝吗?(选自教材P26做一做T1)
3.14×( ) ×15=753.6(cm )
1L=1000mL=1000cm
753.6cm <1000cm ,不够。
8
2
小试牛刀
1.填空题。
(1)把一个高4dm的圆柱截成两个小圆柱后,表面积增加了18cm ,这个圆柱原来的体积是( )cm 。
(2)一个圆柱的体积是108dm ,底面积是18dm ,它的高是( )dm。
360
6
2.计算下面各圆柱的体积。
(1)底面积是25.12dm ,高是6dm。
25.12×6=150.72(dm )
(2)
(8÷2) ×3.14×9=452.16(dm )
3.李家庄挖了一口圆柱形水井,地面以下的井深10 m,底面直径为1 m。挖出的土有多少立方米?(选自教材P25做一做T2)
3.14×( ) ×10=7.85(m )
答:挖出的土有7.85立方米。
1
2
4.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m 。这根木料最多能做多少张课桌?(选自教材P26做一做T2)
3.14×( ) ×5=0.628(m )
0.628÷0.02≈31(张)
答:这根木料最多能做31张课桌。
0.4
2
5.一个圆柱形的钢材,体积是2.512 m ,横截面的半径是0.4 m,这根钢材有多长?
2.512÷(0.42×3.14)=5(m)
答:这根钢材有5 米长。
6.小方一天要喝800 mL水,下图是她上学带水的杯子,从里面量高12厘米,底面直径8厘米。你认为小方需要换带水的杯子吗?
(8÷2) ×3.14×12=602.88(cm )=602.88(mL)
602.88<800,
需要换带水的杯子。
圆柱的体积=底面积×高,用字母表示是 V=Sh,圆柱的底面积=πr ,所以 V=πr h。
容积是容器所能容纳物体的体积,圆柱形容器的容积求法和圆柱体积的求法是一样的,只是所需的数据要从容器的里面量。
作业1:预习下一课。
作业2:完成教材详解对应的练习题。
3.3 圆柱的体积
1. 探索圆柱的体积计算公式,会运用公式计算圆柱的体积。(重点)
2. 能运用圆柱体积计算公式解决实际问题,体会转化思想的实际应用。(难点)
怎样求圆的面积 圆的面积公式是什么
圆的面积=圆周率×半径的平方
字母公式:S = πr
知识点1
圆柱体积的意义及计算公式
5
还可以把圆柱的底面平均分成32份、64份……分成的扇形越多,拼成的立体图形就越接近于长方体。
→
比较拼成的长方体与原来的圆柱,可以发现长方体的底面积等于圆柱的底面积,长方体的高等于圆柱的高。
→
圆柱的体积= 底面积 × 高
长方体的体积= 底面积 × 高
V =
S ×
h
如果知道圆柱的底面半径 r 和高 h,
则V=πr h。
→
圆柱的体积=底面积×高,用字母表示是 V=Sh,圆柱的底面积=πr ,所以 V=πr h。
知识提炼
小试牛刀
一根圆柱形木料,底面积为75cm ,长90cm。它的
体积是多少?(选自教材P25做一做T1)
75×90=6750(cm )
答:它的体积是6750 立方厘米。
知识点2
圆柱体积计算公式的实际应用
6
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
容积的计算方法与体积的计算方法相同。
杯子的底面积:
3.14×(8÷2)2
=3.14×42
=3.14×16
=50.24 (cm2 )
杯子的容积:
50.24×10
=502.4 (cm3 )
=502.4 (mL)
答:因为502.4 大于498,所以杯子能装下这袋牛奶。
容积是容器所能容纳物体的体积,圆柱形容器的容积求法和圆柱体积的求法是一样的,只是所需的数据要从容器的里面量。
知识提炼
小明和妈妈出去游玩,带了一个圆柱形保温杯,
从里面量底面直径是8cm,高是15cm。如果两
人游玩期间要喝 1L水,带这杯水够喝吗?(选自教材P26做一做T1)
3.14×( ) ×15=753.6(cm )
1L=1000mL=1000cm
753.6cm <1000cm ,不够。
8
2
小试牛刀
1.填空题。
(1)把一个高4dm的圆柱截成两个小圆柱后,表面积增加了18cm ,这个圆柱原来的体积是( )cm 。
(2)一个圆柱的体积是108dm ,底面积是18dm ,它的高是( )dm。
360
6
2.计算下面各圆柱的体积。
(1)底面积是25.12dm ,高是6dm。
25.12×6=150.72(dm )
(2)
(8÷2) ×3.14×9=452.16(dm )
3.李家庄挖了一口圆柱形水井,地面以下的井深10 m,底面直径为1 m。挖出的土有多少立方米?(选自教材P25做一做T2)
3.14×( ) ×10=7.85(m )
答:挖出的土有7.85立方米。
1
2
4.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m 。这根木料最多能做多少张课桌?(选自教材P26做一做T2)
3.14×( ) ×5=0.628(m )
0.628÷0.02≈31(张)
答:这根木料最多能做31张课桌。
0.4
2
5.一个圆柱形的钢材,体积是2.512 m ,横截面的半径是0.4 m,这根钢材有多长?
2.512÷(0.42×3.14)=5(m)
答:这根钢材有5 米长。
6.小方一天要喝800 mL水,下图是她上学带水的杯子,从里面量高12厘米,底面直径8厘米。你认为小方需要换带水的杯子吗?
(8÷2) ×3.14×12=602.88(cm )=602.88(mL)
602.88<800,
需要换带水的杯子。
圆柱的体积=底面积×高,用字母表示是 V=Sh,圆柱的底面积=πr ,所以 V=πr h。
容积是容器所能容纳物体的体积,圆柱形容器的容积求法和圆柱体积的求法是一样的,只是所需的数据要从容器的里面量。
作业1:预习下一课。
作业2:完成教材详解对应的练习题。
