人教数学六年级下第3单元 圆柱与圆锥整理和复习 课件(26张ppt)
文档属性
| 名称 | 人教数学六年级下第3单元 圆柱与圆锥整理和复习 课件(26张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 910.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第3单元整理和复习
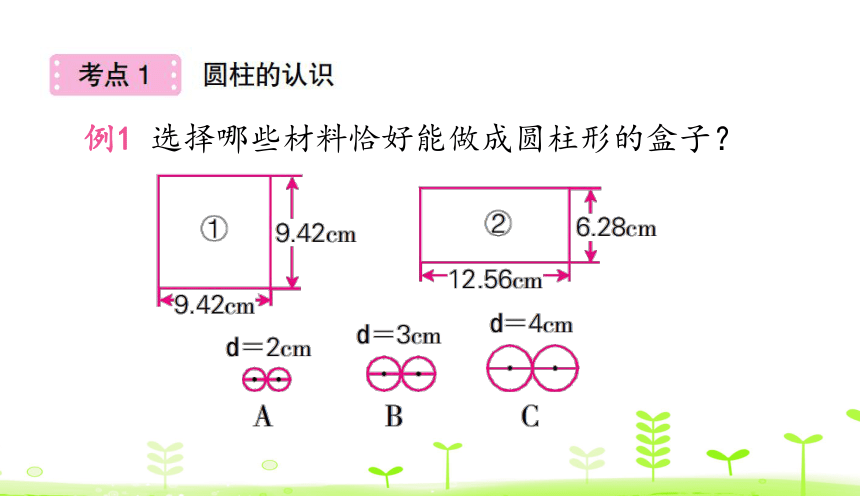
例1 选择哪些材料恰好能做成圆柱形的盒子?
思路分析:圆柱的侧面沿高剪开的展开图是一个长方形或正方形,这个长方形的长(宽)或正方形的边长等于圆柱的底面周长,所以只要每组两个等圆中的一个圆的周长等于长方形的长(宽)或正方形的边长,那么这组圆就能和这个长方形或正方形做成圆柱形的盒子。
计算对比:2×3.14=6.28(cm),3×3.14=
9.42(cm),4×3.14=12.56(cm),因此,①和
B、②和A或②和C都能做成圆柱形的盒子。
解答此类题的关键是明确长方形的长(宽)或正方形的边长等于圆柱的底面周长,根据公式 C=2πr 或C=πd求出圆的周长,然后与长方形的长(宽)或正方形的边长进行比较即可确定答案。
规范解答:选择①和B、②和A或②和C都恰好能做成圆柱形的盒子。
1.把圆柱的侧面沿高展开,得到一个( ),它的长等于圆柱底面的( ),宽等于圆柱的( )。
长方形
周长
高
例2 做一个无盖的圆柱形铁皮容器,底面半径是3dm,高是4dm,做这个容器至少需要多少平方分米铁皮?
思路分析:要求至少需要多少平方分米的铁皮,就是求容器的表面积。要求容器的表面积,先要明确容器的表面积包括哪几部分。由于容器没有盖,所以计算表面积时,底面积只有一个,即容器的表面积等于侧面积加上一个底面积。
规范解答:容器的侧面积:
2×3.14×3×4=75.36(dm )
容器的底面积:
3.14×3 =28.26(dm )
容器的表面积:
75.36+28.26=103.62(dm )
答:做这个容器至少需要103.62平方分米铁皮。
2.刘师傅要用铁皮做一个无盖的圆柱形水桶,水桶的底面半径为20cm,高为60cm。做这个水桶至少需要多少铁皮?
20×2×3.14×60+202×3.14=8792(cm )
答:做这个水桶至少需要8792平方厘米铁皮。
例3 一根钢管,长50厘米,外圆直径是10厘米,钢管厚2cm(如下图)。铸造这样一根钢管需要钢材多少立方厘米?
思路分析:求铸造这样一根钢管需要钢材的体积,就是用大圆柱的体积减去中空的小圆柱的体积。
规范解答:大圆柱的半径:
10÷2=5(厘米)
中空部分圆柱的半径:
5-2=3(厘米)
需要钢材的体积:
3.14×(5 -3 )×50=2512(立方厘米)
答:铸造这样一根钢管需要钢材2512立方厘米。
例4 有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是480mL,现在瓶中装有一些饮料。瓶子正放时饮料的高度为20cm,倒放时空余部分的高度为4cm(如下图)。瓶内现有饮料多少毫升?
思路分析:瓶子正放和倒放时的容积与饮料的体积不变,所以瓶子空余部分的容积相等。因此,饮料瓶的容积就相当于一个高为(20+4)cm 的圆柱形容器的容积,可推知饮料体积占瓶子容积的 ,即 480mL的 。
确定瓶中饮料的体积占瓶子容积的几分之几是解答此题的关键。
规范解答:20+4=24(cm)
480× =400(mL)
答:瓶内现有饮料400毫升。
3.一个内半径是10cm的饮料瓶里,饮料的高度为4cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度为16cm,这个瓶子的容积是多少?
102×3.14×(16+4)=6280(cm )=6280(mL)
答:这个瓶子的容积是6280毫升。
例5 天坛祈年殿塔的顶端近似于圆锥形,它的底面周长是18.84m,高是6m,求塔的顶端的体积。
思路分析:塔的顶端呈圆锥形,求塔的顶端的体积就是求圆锥的体积。计算时先根据公式S底=π 求出圆锥的底面积,再根据公式V 求出圆锥的体积。
规范解答::圆锥的底面积:
3.14×(18.84÷3.14÷2)
=3.14×9
=28.26(m )
圆锥的体积:
×28.26×6
=2×28.26
=56.52(m )
答:塔的顶端的体积是 56.52立方米。
4.一个圆锥形麦堆,底面直径为3m,高为2.5m。
(1)它的占地面积是多少平方米?
(3÷2) ×3.14=7.065(m )
答:它的占地面积是7.065平方米。
(2)它的体积是多少立方米?
7.065×2.5× =5.8875(m )
答:它的体积是5.8875立方米。
1
3
第3单元整理和复习
例1 选择哪些材料恰好能做成圆柱形的盒子?
思路分析:圆柱的侧面沿高剪开的展开图是一个长方形或正方形,这个长方形的长(宽)或正方形的边长等于圆柱的底面周长,所以只要每组两个等圆中的一个圆的周长等于长方形的长(宽)或正方形的边长,那么这组圆就能和这个长方形或正方形做成圆柱形的盒子。
计算对比:2×3.14=6.28(cm),3×3.14=
9.42(cm),4×3.14=12.56(cm),因此,①和
B、②和A或②和C都能做成圆柱形的盒子。
解答此类题的关键是明确长方形的长(宽)或正方形的边长等于圆柱的底面周长,根据公式 C=2πr 或C=πd求出圆的周长,然后与长方形的长(宽)或正方形的边长进行比较即可确定答案。
规范解答:选择①和B、②和A或②和C都恰好能做成圆柱形的盒子。
1.把圆柱的侧面沿高展开,得到一个( ),它的长等于圆柱底面的( ),宽等于圆柱的( )。
长方形
周长
高
例2 做一个无盖的圆柱形铁皮容器,底面半径是3dm,高是4dm,做这个容器至少需要多少平方分米铁皮?
思路分析:要求至少需要多少平方分米的铁皮,就是求容器的表面积。要求容器的表面积,先要明确容器的表面积包括哪几部分。由于容器没有盖,所以计算表面积时,底面积只有一个,即容器的表面积等于侧面积加上一个底面积。
规范解答:容器的侧面积:
2×3.14×3×4=75.36(dm )
容器的底面积:
3.14×3 =28.26(dm )
容器的表面积:
75.36+28.26=103.62(dm )
答:做这个容器至少需要103.62平方分米铁皮。
2.刘师傅要用铁皮做一个无盖的圆柱形水桶,水桶的底面半径为20cm,高为60cm。做这个水桶至少需要多少铁皮?
20×2×3.14×60+202×3.14=8792(cm )
答:做这个水桶至少需要8792平方厘米铁皮。
例3 一根钢管,长50厘米,外圆直径是10厘米,钢管厚2cm(如下图)。铸造这样一根钢管需要钢材多少立方厘米?
思路分析:求铸造这样一根钢管需要钢材的体积,就是用大圆柱的体积减去中空的小圆柱的体积。
规范解答:大圆柱的半径:
10÷2=5(厘米)
中空部分圆柱的半径:
5-2=3(厘米)
需要钢材的体积:
3.14×(5 -3 )×50=2512(立方厘米)
答:铸造这样一根钢管需要钢材2512立方厘米。
例4 有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是480mL,现在瓶中装有一些饮料。瓶子正放时饮料的高度为20cm,倒放时空余部分的高度为4cm(如下图)。瓶内现有饮料多少毫升?
思路分析:瓶子正放和倒放时的容积与饮料的体积不变,所以瓶子空余部分的容积相等。因此,饮料瓶的容积就相当于一个高为(20+4)cm 的圆柱形容器的容积,可推知饮料体积占瓶子容积的 ,即 480mL的 。
确定瓶中饮料的体积占瓶子容积的几分之几是解答此题的关键。
规范解答:20+4=24(cm)
480× =400(mL)
答:瓶内现有饮料400毫升。
3.一个内半径是10cm的饮料瓶里,饮料的高度为4cm,把瓶盖拧紧倒置放平,无水部分是圆柱形,高度为16cm,这个瓶子的容积是多少?
102×3.14×(16+4)=6280(cm )=6280(mL)
答:这个瓶子的容积是6280毫升。
例5 天坛祈年殿塔的顶端近似于圆锥形,它的底面周长是18.84m,高是6m,求塔的顶端的体积。
思路分析:塔的顶端呈圆锥形,求塔的顶端的体积就是求圆锥的体积。计算时先根据公式S底=π 求出圆锥的底面积,再根据公式V 求出圆锥的体积。
规范解答::圆锥的底面积:
3.14×(18.84÷3.14÷2)
=3.14×9
=28.26(m )
圆锥的体积:
×28.26×6
=2×28.26
=56.52(m )
答:塔的顶端的体积是 56.52立方米。
4.一个圆锥形麦堆,底面直径为3m,高为2.5m。
(1)它的占地面积是多少平方米?
(3÷2) ×3.14=7.065(m )
答:它的占地面积是7.065平方米。
(2)它的体积是多少立方米?
7.065×2.5× =5.8875(m )
答:它的体积是5.8875立方米。
1
3
