人教数学六下第6单元整理与复习 6.6 立体图形的认识与测量 课件(18张ppt)
文档属性
| 名称 | 人教数学六下第6单元整理与复习 6.6 立体图形的认识与测量 课件(18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 18:09:12 | ||
图片预览





文档简介
(共18张PPT)
6.6 立体图形的认识与测量
1.理解、掌握所学立体图形的特征以及表
面积、体积的计算方法。(重点)
2.运用立体图形的相关知识解决实际问题。
(难点)
立体图形的特征
长方体、正方体的每个面都是平面,圆柱和圆锥都有一个曲面。
长方体和正方体有什么相同点和不同点?
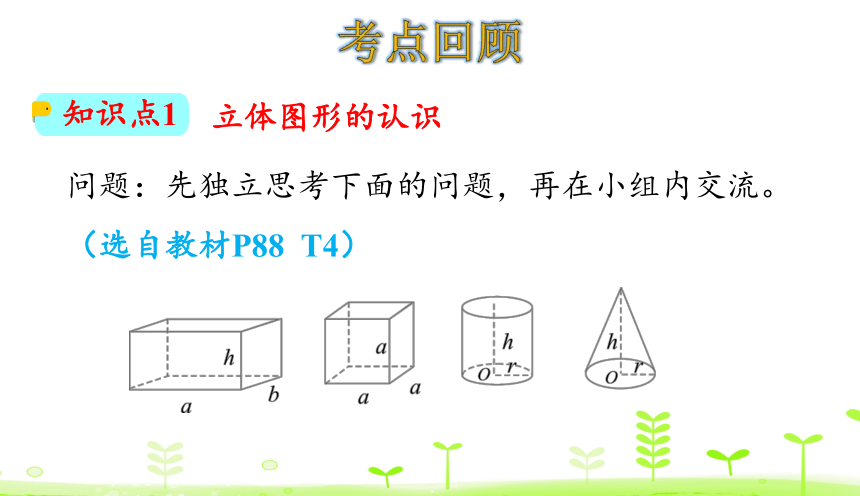
问题:先独立思考下面的问题,再在小组内交流。(选自教材P88 T4)
知识点1
立体图形的认识
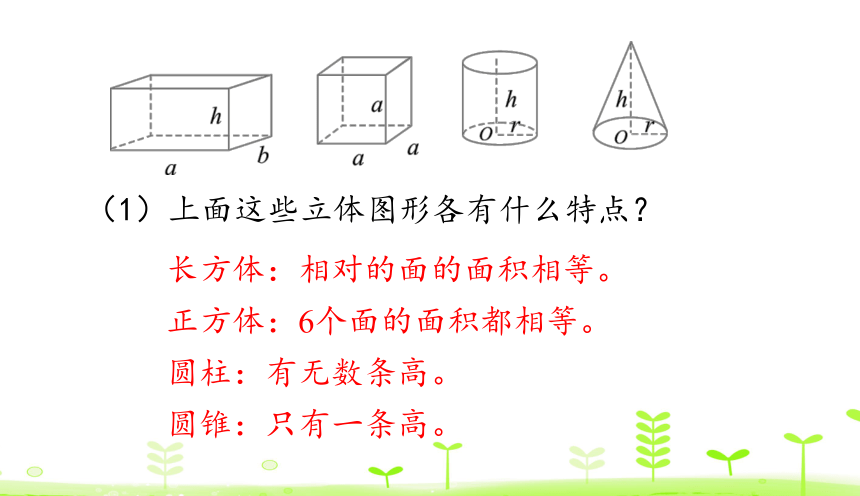
(1)上面这些立体图形各有什么特点?
长方体:相对的面的面积相等。
正方体:6个面的面积都相等。
圆柱:有无数条高。
圆锥:只有一条高。
(2)长方体与正方体有什么相同点和不同点?
长方体与正方体的相同点:
1、都有6个面和12个棱。
2、相对的面互相平行、相对的棱互相平行。
3、相邻的三条棱互相垂直。
(2)长方体与正方体有什么相同点和不同点?
长方体与正方体的不同点:
1、正方体的所有棱长相等,而长方体只有相对的棱长相等;
2、正方体是特殊的长方体。
(3)圆柱与圆锥可以各由什么平面图形旋转而成?
圆柱是由长方形以长(或宽)为轴或正方形以边长为轴旋转而成的。
圆锥是由直角三角形以直角边为轴旋转而成的。
(4)圆柱和圆锥之间有什么关系?
圆柱的上、下两个底面是大小相等的圆,侧面是一个曲面,有无数条高。
圆锥的底面是一个圆,侧面是一个曲面,只有一条高。
圆柱的体积是与其等底等高的圆锥的体积的3倍。
(选自教材P88 T5)
知识点2
立体图形的表面积和体积
立体图形的表面积计算公式的内在联系:长方体和圆柱体的表面积都可以用侧面积加两个底面积求得。
立体图形的体积计算公式的内在联系:有长方体体积计算公式推导出了正方体和圆柱的体积计算公式。长方体、正方体、圆柱体积都可以用“底面积×高”来求得。
1.(选自教材P88 做一做T1)
可以将马铃薯完全浸没在盛有适量的水、并已知
底面积的圆柱形容器里面,观察水面上升的高度,
将求马铃薯的体积转化为求圆柱的体积。
2.在方格纸上分别画出从不同方向看到左边立体图形的形状图。(选自教材P88 做一做T2)
3.把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?(选自教材P90 T11)
(6÷2)×(6÷2)×(6÷2)=27(个)
6×6×2×6=432(cm )
4.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)(选自教材P91 T12)
10×10×10÷[ ×3.14×( ) ]≈10(cm)
答:这个圆锥形铁块的高约是10cm。
1
3
20
2
5.一块正方形菜地,一边靠墙,其余三边围上总长度
为 27 米的竹篱笆,这块正方形菜地的面积是多少平
方米?
27÷3=9(米)
9×9=81(平方米)
答:这块正方形菜地的面积是81平方米。
作业1:完成教材相关练习题。
作业2:完成教材详解对应的练习题。
6.6 立体图形的认识与测量
1.理解、掌握所学立体图形的特征以及表
面积、体积的计算方法。(重点)
2.运用立体图形的相关知识解决实际问题。
(难点)
立体图形的特征
长方体、正方体的每个面都是平面,圆柱和圆锥都有一个曲面。
长方体和正方体有什么相同点和不同点?
问题:先独立思考下面的问题,再在小组内交流。(选自教材P88 T4)
知识点1
立体图形的认识
(1)上面这些立体图形各有什么特点?
长方体:相对的面的面积相等。
正方体:6个面的面积都相等。
圆柱:有无数条高。
圆锥:只有一条高。
(2)长方体与正方体有什么相同点和不同点?
长方体与正方体的相同点:
1、都有6个面和12个棱。
2、相对的面互相平行、相对的棱互相平行。
3、相邻的三条棱互相垂直。
(2)长方体与正方体有什么相同点和不同点?
长方体与正方体的不同点:
1、正方体的所有棱长相等,而长方体只有相对的棱长相等;
2、正方体是特殊的长方体。
(3)圆柱与圆锥可以各由什么平面图形旋转而成?
圆柱是由长方形以长(或宽)为轴或正方形以边长为轴旋转而成的。
圆锥是由直角三角形以直角边为轴旋转而成的。
(4)圆柱和圆锥之间有什么关系?
圆柱的上、下两个底面是大小相等的圆,侧面是一个曲面,有无数条高。
圆锥的底面是一个圆,侧面是一个曲面,只有一条高。
圆柱的体积是与其等底等高的圆锥的体积的3倍。
(选自教材P88 T5)
知识点2
立体图形的表面积和体积
立体图形的表面积计算公式的内在联系:长方体和圆柱体的表面积都可以用侧面积加两个底面积求得。
立体图形的体积计算公式的内在联系:有长方体体积计算公式推导出了正方体和圆柱的体积计算公式。长方体、正方体、圆柱体积都可以用“底面积×高”来求得。
1.(选自教材P88 做一做T1)
可以将马铃薯完全浸没在盛有适量的水、并已知
底面积的圆柱形容器里面,观察水面上升的高度,
将求马铃薯的体积转化为求圆柱的体积。
2.在方格纸上分别画出从不同方向看到左边立体图形的形状图。(选自教材P88 做一做T2)
3.把一个棱长6cm的正方体切成棱长2cm的小正方体。可以得到多少个小正方体?它们的表面积之和比原来大正方体的表面积增加了多少?(选自教材P90 T11)
(6÷2)×(6÷2)×(6÷2)=27(个)
6×6×2×6=432(cm )
4.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米。)(选自教材P91 T12)
10×10×10÷[ ×3.14×( ) ]≈10(cm)
答:这个圆锥形铁块的高约是10cm。
1
3
20
2
5.一块正方形菜地,一边靠墙,其余三边围上总长度
为 27 米的竹篱笆,这块正方形菜地的面积是多少平
方米?
27÷3=9(米)
9×9=81(平方米)
答:这块正方形菜地的面积是81平方米。
作业1:完成教材相关练习题。
作业2:完成教材详解对应的练习题。
