人教数学六下第6单元整理与复习 6.10 数学思考 课件(19张ppt)
文档属性
| 名称 | 人教数学六下第6单元整理与复习 6.10 数学思考 课件(19张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 18:02:29 | ||
图片预览






文档简介
(共19张PPT)
6.10 数学思考
1.通过画图,使学生能发现规律,总结规律。
(重点)
2.培养学生的逻辑推理能力。(难点)
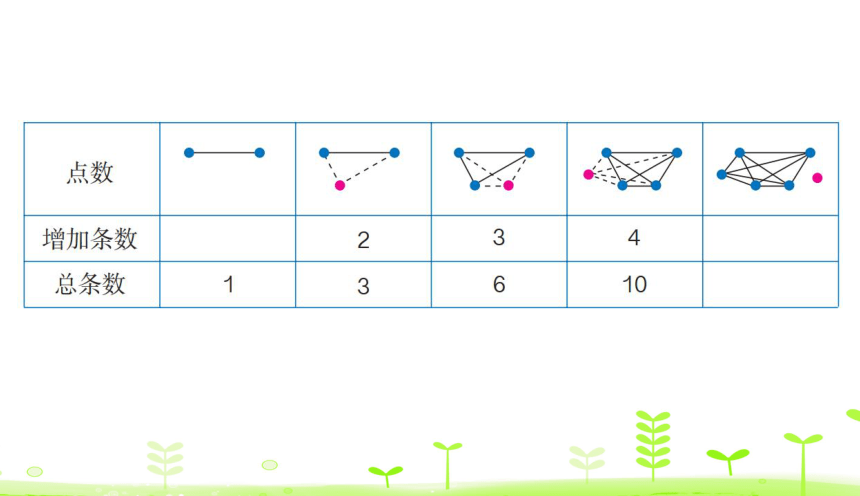
6 个点可以连多少条线段? 8 个点呢?
1+2+3+4+5=15(条)
3 个点连成线段的条数:1+2=3(条)
4 个点连成线段的条数:1+2+3=6(条)
5 个点连成线段的条数:1+2+3+4=10(条)
6 个点连成线段的条数:
8 个点连成线段的条数:
1+2+3+4+5+6+7=28(条)
根据规律,你知道12个点、 20 个点能连多少条线段吗?请写出算式。
12个点连成线段的条数:
1+2+3+4+5+6+7+8+9+10+11
=(1+11)×11÷2=66(条)
20个点连成线段的条数:
1+2+3+4+5+6+……+18+19
=(1+19)×19÷2=190(条)
n个点连成线段的条数:
1+2+3+4+……+(n-2)+(n-1)
=(1+n-1)×(n-1)÷2
= (条)
答:6个点可以连15条线段;12个点可以连66条线段;20个点可以连190条线段;n个点可以连
条线段。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的
这个问题好复杂呀!
用列表的方
法试一试!
知识点1
逻辑推理
用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A和D B和F C和E
1.△、□、○、◇、◎各代表一个数。
(1)已知△+□=24, △=□+□+□。求△和□的值。
已知△+□=24,△=□+□+□,可得□+□+□+□=24,即4×□=24,所以□=6。△=□+□+□=18。
一个△等于三个□的和。
把△+□=24中的△换成□+□+□,这叫等量代换。
知识点2
等量代换
(2)已知○+◇=160, ◎+◇=160。○是否等于◎?
已知○+◇=160,◎+◇=160。根据等式的性质,等式两边都减去◇,可以推出,○=160-◇,◎=160-◇。
因为◇代表同一个数,所以○=◎。
两个等式
里都有◇。
可以利用等
式的性质。
什么是平角?平角与直线有什么区别?如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平
角,一共能组成几个平角?
知识点3
平角与直线
想:平角的两边在一条直线上。
∠1和∠2,∠2和∠3,∠3和∠4,
∠4和∠1,一共能组成4个平角。
(2)你能推出∠1=∠3吗?
想:∠1和∠2,∠2和∠3,都能组成平角。
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2°,∠3=180°-∠2°。
因为180°-∠2°=180°-∠2°,所以∠1=∠3。
那接下来怎么办呢?
把∠1和∠2,∠2和∠3的关系用等式表示出来。
问题:1. 你想怎样解决这个问题?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
7×7=49(个)
15×15=225(个)
(1)第7幅图有多少个棋子?第15幅图呢?
(2)第n幅图有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
2.王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。请问:他们的职业各是什么?
王阿姨的职业是教师,丁叔叔的职业是军人,刘阿姨的职业是工人,李叔叔的职业也是工人。
3.找规律,填数。
41
(1)3,11,20,30, ,53, ,
(2)1,3,2,6,4,9,8, , ,
15, ,18,
66
12
16
32
作业1:完成教材相关练习题。
作业2:完成教材详解对应的练习题。
6.10 数学思考
1.通过画图,使学生能发现规律,总结规律。
(重点)
2.培养学生的逻辑推理能力。(难点)
6 个点可以连多少条线段? 8 个点呢?
1+2+3+4+5=15(条)
3 个点连成线段的条数:1+2=3(条)
4 个点连成线段的条数:1+2+3=6(条)
5 个点连成线段的条数:1+2+3+4=10(条)
6 个点连成线段的条数:
8 个点连成线段的条数:
1+2+3+4+5+6+7=28(条)
根据规律,你知道12个点、 20 个点能连多少条线段吗?请写出算式。
12个点连成线段的条数:
1+2+3+4+5+6+7+8+9+10+11
=(1+11)×11÷2=66(条)
20个点连成线段的条数:
1+2+3+4+5+6+……+18+19
=(1+19)×19÷2=190(条)
n个点连成线段的条数:
1+2+3+4+……+(n-2)+(n-1)
=(1+n-1)×(n-1)÷2
= (条)
答:6个点可以连15条线段;12个点可以连66条线段;20个点可以连190条线段;n个点可以连
条线段。
六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的
这个问题好复杂呀!
用列表的方
法试一试!
知识点1
逻辑推理
用数字“1”表示到会,用数字“0”表示没到会。
A B C D E F
第一次 1 1 1 0 0 0
第二次 0 1 0 1 1 0
第三次 1 0 0 0 1 1
A和D B和F C和E
1.△、□、○、◇、◎各代表一个数。
(1)已知△+□=24, △=□+□+□。求△和□的值。
已知△+□=24,△=□+□+□,可得□+□+□+□=24,即4×□=24,所以□=6。△=□+□+□=18。
一个△等于三个□的和。
把△+□=24中的△换成□+□+□,这叫等量代换。
知识点2
等量代换
(2)已知○+◇=160, ◎+◇=160。○是否等于◎?
已知○+◇=160,◎+◇=160。根据等式的性质,等式两边都减去◇,可以推出,○=160-◇,◎=160-◇。
因为◇代表同一个数,所以○=◎。
两个等式
里都有◇。
可以利用等
式的性质。
什么是平角?平角与直线有什么区别?如右图,两条直线相交于点O。
(1)每相邻两个角可以组成一个平
角,一共能组成几个平角?
知识点3
平角与直线
想:平角的两边在一条直线上。
∠1和∠2,∠2和∠3,∠3和∠4,
∠4和∠1,一共能组成4个平角。
(2)你能推出∠1=∠3吗?
想:∠1和∠2,∠2和∠3,都能组成平角。
根据第(1)题的结论,可以得到∠1+∠2=180°,∠2+∠3=180°。
根据等式的性质,等式的两边都减去∠2,可以得到∠1=180°-∠2°,∠3=180°-∠2°。
因为180°-∠2°=180°-∠2°,所以∠1=∠3。
那接下来怎么办呢?
把∠1和∠2,∠2和∠3的关系用等式表示出来。
问题:1. 你想怎样解决这个问题?
每行的棋子数×行数=棋子总数
1×1 2×2 3×3 4×4
1 4 9 16
1.观察下图,想一想。
(1)第7幅图有多少个棋子?第15幅图呢?
7×7=49(个)
15×15=225(个)
(1)第7幅图有多少个棋子?第15幅图呢?
(2)第n幅图有多少个棋子?
每行的棋子数×行数=棋子总数
n×n=棋子总数
n2=棋子总数
2.王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。请问:他们的职业各是什么?
王阿姨的职业是教师,丁叔叔的职业是军人,刘阿姨的职业是工人,李叔叔的职业也是工人。
3.找规律,填数。
41
(1)3,11,20,30, ,53, ,
(2)1,3,2,6,4,9,8, , ,
15, ,18,
66
12
16
32
作业1:完成教材相关练习题。
作业2:完成教材详解对应的练习题。
