人教版数学六年级下册期末复习课件-6.1.4 比和比例 课件(51张PPT)
文档属性
| 名称 | 人教版数学六年级下册期末复习课件-6.1.4 比和比例 课件(51张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览










文档简介
(共51张PPT)
6.1.4 比和比例
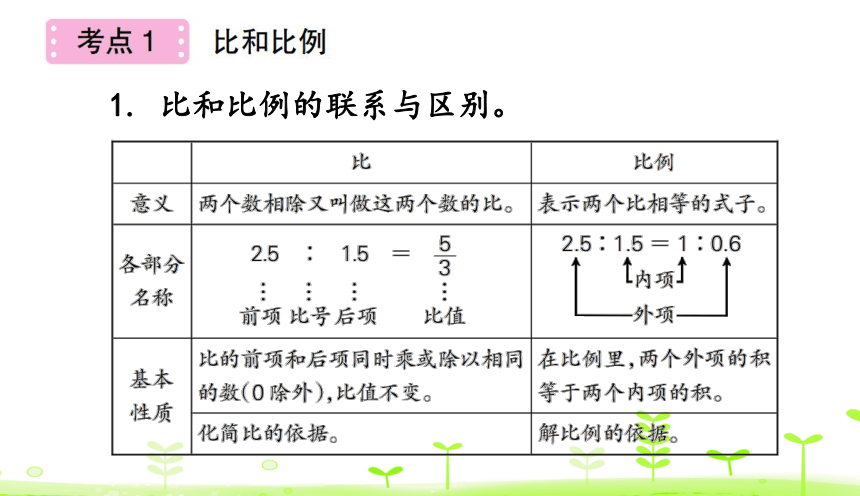
1. 比和比例的联系与区别。
2. 比与分数、除法的联系。
3. 比与分数、除法之间的区别。
(1)比表示两个数之间的倍比关系。
(2)分数是一个数。
(3)除法是一种运算。
4. 比的基本性质、分数的基本性质、商不变的规律之间的联系。
比的基本性质:比的前项和后项同时乘或除以相同的数(0 除外),比值不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0 除外),分数的大小不变。
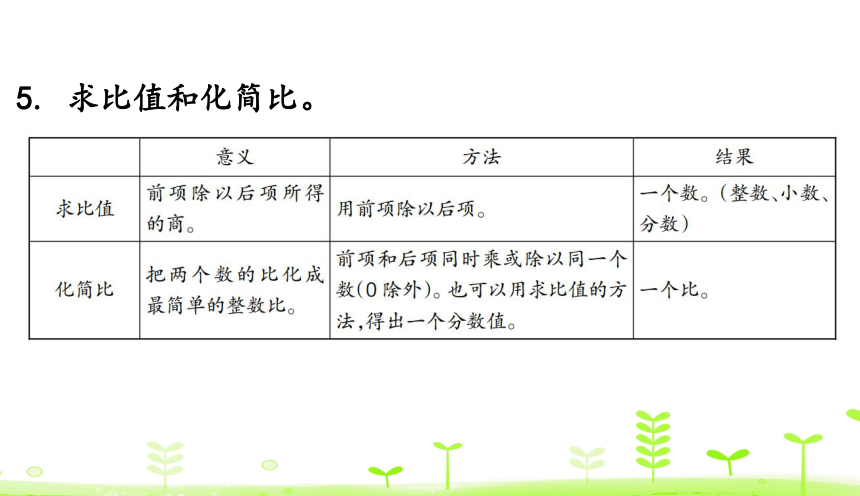
5. 求比值和化简比。
例 1 把下面的比化成最简整数比,再求出比值。
(2)0.25∶1
过程讲解
将 化成最简整数比,可以先根据比的基本性质,将比的前项和后项都乘32,得到9∶18,然后再将比的前项和后项同时除以9,得到1∶2。同理0.25∶1=(0.25×4)∶(1×4)=1∶4。求比值用比的前项除以后项,求出商即可。
解答:(1)
解答:(2)
0.25∶1=(0.25×4)∶(1×4)=1∶4
0.25∶1=0.25÷1=0.25
例 2 解比例。
过程讲解
(1)根据比例的基本性质(两个内项的积等于两个外项的积),可得3x×0.8=4×1.8,再按解方程的方法解答。
(2)根据比例的基本性质,先将原比例式转化为
=5×0.75,再解方程。
实战演练 1
1. 填空题。
(1)在比例中,若两个外项互为倒数,其中一个内
项是 另一个内项是( )。
(2)在含糖25%的糖水中,糖与水的比是( )。
3
16
1:3
(3)若x的 等于y的 则x∶y=( )∶( ),
当x=240时,y=( )。
(4)一个长方形的长与宽的比是2∶1,则宽是长的
( )。
10
7
168
1
2
2. 解比例。
x=
3
x=
8
1. 认识正比例和反比例。
2. 正、反比例的异同。
例 下面各题中的两种量是不是成比例?如果成比例,成什么比例关系?
(1)订鲜牛奶的份数和钱数。
(2)在一定时间里,制作蛋糕的盒数和制作一盒蛋糕所需的时间。
(3)正方体的棱长和体积。
过程讲解
(1)订鲜牛奶的份数和钱数,这两种相关联的量与鲜牛奶的单价(定量)之间的关系:
订鲜牛奶的钱数÷份数=鲜牛奶的单价(一定)
所以订鲜牛奶的份数和钱数成正比例关系。
(2)制作蛋糕的盒数和制作一盒蛋糕所需的时间,这两种相关联的量与制作蛋糕所用的总时间(定量)之间的关系:
制作一盒蛋糕所需时间×制作蛋糕的盒数=总时间(一定)
所以制作蛋糕的盒数和制作一盒蛋糕所需的时间成反比例关系。
(3)正方体的棱长和体积,这两种相关联的量有如下关系:
体积÷棱长=棱长×棱长(不一定)
因为棱长是变量,那么棱长与棱长的乘积也是变化的,所以正方体的体积与棱长不成比例。
解答:(1)成正比例关系 (2)成反比例关系
(3)不成比例
实战演练 2
判断下面每组中的量成不成比例,成什么比例。
(1)圆的半径和面积。
(2)积一定(0除外),两个因数。
不成比例
成反比例
(3)出油率一定,油的质量和所需花生的质量。
(4)总人数一定,出勤人数和缺勤人数。
成正比例
不成比例
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺,即比例尺= 比例尺有两种形式:数值比例尺和线段比例尺。
例 1 某公园有一块100米长的草坪,画在平面图上只有2厘米。这幅公园平面图的比例尺是多少?
过程讲解
求比例尺时,可根据“比例尺=图上距离∶实际距离”进行求解。
解答:100米=10000厘米
2厘米∶10000厘米=1∶5000
答:这幅公园平面图的比例尺是1∶5000。
例 2 在比例尺是1∶5000000的地图上,量得甲、乙两地间的距离为3.6厘米。如果王叔叔开车从甲地出发以每小时60千米的速度行驶,几小时可以到达乙地?
过程讲解
已知图上距离和比例尺,根据“实际距离=图上距离÷比例尺”求出实际距离,即甲、乙两地间的路程。再根据“路程÷速度=时间”,求出王叔叔需要行驶的时间。
解答:3.6÷ =3.6×5000000=18000000(厘米)
18000000 厘米=180千米
180÷60=3(小时)
答:3 小时可以到达乙地。
实战演练 3
在一幅地图上,用3厘米的线段表示实际距离900千米。
(1)这幅地图的比例尺是多少?
1∶30000000
(2)一条长480千米的高速公路,在这幅地图上是多少厘米?
1.6厘米
1. 按一定的比分配问题。
(1)按一定的比分配的应用题:把一个数量按照一定的比分配成几部分,求每部分数量各是多少的应用题。
(2)解题方法。
一般方法:把比转化成分数,用分数方法解答,即先求总份数,再求各部分占总量的几分之几,最后按求一个数的几分之几是多少,用乘法计算,求出各部分的量是多少。
归一法:把比看作分得的份数,先求出总份数,然后用“总量÷总份数=平均每份的量”求出每份的量,再用“每份的量×各部分量所对应的份数”求出各部分的量。
用比例知识解答:首先设未知量为x,根据题中“已知比等于相对应的量的比”作为等量关系式,列出含有 x的比例式,再解比例求出x。
2. 用正、反比例知识解答应用题的步骤。
(1)分析数量关系。判断成什么比例。
(2)找等量关系。如果是成正比例,则按“等比”找等量关系式;如果是成反比例,则按“等积”找等量关系式。
(3)列比例式。设未知数为 x,根据等量关系式列出正比例式或反比例式。
(4)解比例。
(5)检验并写答语。
例 1 美术小组一共有45人,其中男生和女生的人数比为2∶3。美术小组男生和女生各有多少人?
过程讲解
我们可以这样想,男生和女生的人数比为2∶3,可以把男生人数看作2份,女生人数看作3份,美术小组总人数对应的总份数就是2+3=5(份),我们可以求出每份的人数为45÷5=9(人),男生有9×2=18(人),女生有9×3=27(人)。
我们也可以利用分数的相关知识来解决,因为男生和女生的人数比2∶3,所以男生占总人数的
女生占总人数的 根据分数乘法的意义,男生的人数为45× =18(人),女生的人数为45×
=27(人)。
解答:方法一 2+3=5(份) 45÷5=9(人)
男生:9×2=18(人)
女生:9×3=27(人)
方法二 男生:45× =18(人)
女生:45× =27(人)
答:美术小组男生有 18 人,女生有 27 人。
例 2 修路队修一条公路,原计划每天修1200米,50天可以修完。实际每天修2400米,实际需要多少天完成?
过程讲解
这道题中,每天修的米数和修的天数是两种相关联的量,因为“每天修的米数×修的天数=路的长度”,而路的长度一定,所以每天修的米数和修的天数成反比例关系,因此,我们可以根据反比例的意义列出等式并解答。
解答:解:设实际需要x天完成。
2400x=1200×50
2400x=60000
x=25
答:实际需要25天完成。
例 3 某修路队要修一段长28.8千米的公路,前4天修了7.2千米,照这样计算,剩下的还要多少天修完?(用比例解)
过程讲解
“照这样计算”就是说每天修路的长度是一定的,所以修路长度和修路天数成正比例关系。因此,我们可以根据正比例的意义列出等式并解答。
解答:解:设剩下的还要x天修完。
7.2x=4×(28.8-7.2)
7.2x=86.4
x=12
答:剩下的还要12天修完。
实战演练 4
1. 一种灭蝇药,用药液和水按1∶1500配制而成,要配制这种药水750.5千克,需要药液与水各多少千克?
需要药液0.5kg,水750kg。
2. 测量小组要测量一棵树的高度。量得树的影长是8.4米,同一时间量得附近一根2米长的直立竹竿的影长是1.2米。这棵树的高度是多少米?
14米
3. 装修一间客厅,用边长5dm的方砖铺地,需要 80块,如果改用边长4dm的方砖铺地,需要多少块?
(用比例解)
125块
4. 某售楼处销售一处新建楼房,计划每天销售30 套,12天售完。实际平均每天多售6套,实际比计划少
用多少天售完全部楼房?
2天
6.1.4 比和比例
1. 比和比例的联系与区别。
2. 比与分数、除法的联系。
3. 比与分数、除法之间的区别。
(1)比表示两个数之间的倍比关系。
(2)分数是一个数。
(3)除法是一种运算。
4. 比的基本性质、分数的基本性质、商不变的规律之间的联系。
比的基本性质:比的前项和后项同时乘或除以相同的数(0 除外),比值不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0 除外),分数的大小不变。
5. 求比值和化简比。
例 1 把下面的比化成最简整数比,再求出比值。
(2)0.25∶1
过程讲解
将 化成最简整数比,可以先根据比的基本性质,将比的前项和后项都乘32,得到9∶18,然后再将比的前项和后项同时除以9,得到1∶2。同理0.25∶1=(0.25×4)∶(1×4)=1∶4。求比值用比的前项除以后项,求出商即可。
解答:(1)
解答:(2)
0.25∶1=(0.25×4)∶(1×4)=1∶4
0.25∶1=0.25÷1=0.25
例 2 解比例。
过程讲解
(1)根据比例的基本性质(两个内项的积等于两个外项的积),可得3x×0.8=4×1.8,再按解方程的方法解答。
(2)根据比例的基本性质,先将原比例式转化为
=5×0.75,再解方程。
实战演练 1
1. 填空题。
(1)在比例中,若两个外项互为倒数,其中一个内
项是 另一个内项是( )。
(2)在含糖25%的糖水中,糖与水的比是( )。
3
16
1:3
(3)若x的 等于y的 则x∶y=( )∶( ),
当x=240时,y=( )。
(4)一个长方形的长与宽的比是2∶1,则宽是长的
( )。
10
7
168
1
2
2. 解比例。
x=
3
x=
8
1. 认识正比例和反比例。
2. 正、反比例的异同。
例 下面各题中的两种量是不是成比例?如果成比例,成什么比例关系?
(1)订鲜牛奶的份数和钱数。
(2)在一定时间里,制作蛋糕的盒数和制作一盒蛋糕所需的时间。
(3)正方体的棱长和体积。
过程讲解
(1)订鲜牛奶的份数和钱数,这两种相关联的量与鲜牛奶的单价(定量)之间的关系:
订鲜牛奶的钱数÷份数=鲜牛奶的单价(一定)
所以订鲜牛奶的份数和钱数成正比例关系。
(2)制作蛋糕的盒数和制作一盒蛋糕所需的时间,这两种相关联的量与制作蛋糕所用的总时间(定量)之间的关系:
制作一盒蛋糕所需时间×制作蛋糕的盒数=总时间(一定)
所以制作蛋糕的盒数和制作一盒蛋糕所需的时间成反比例关系。
(3)正方体的棱长和体积,这两种相关联的量有如下关系:
体积÷棱长=棱长×棱长(不一定)
因为棱长是变量,那么棱长与棱长的乘积也是变化的,所以正方体的体积与棱长不成比例。
解答:(1)成正比例关系 (2)成反比例关系
(3)不成比例
实战演练 2
判断下面每组中的量成不成比例,成什么比例。
(1)圆的半径和面积。
(2)积一定(0除外),两个因数。
不成比例
成反比例
(3)出油率一定,油的质量和所需花生的质量。
(4)总人数一定,出勤人数和缺勤人数。
成正比例
不成比例
一幅图的图上距离和实际距离的比,叫做这幅图的比例尺,即比例尺= 比例尺有两种形式:数值比例尺和线段比例尺。
例 1 某公园有一块100米长的草坪,画在平面图上只有2厘米。这幅公园平面图的比例尺是多少?
过程讲解
求比例尺时,可根据“比例尺=图上距离∶实际距离”进行求解。
解答:100米=10000厘米
2厘米∶10000厘米=1∶5000
答:这幅公园平面图的比例尺是1∶5000。
例 2 在比例尺是1∶5000000的地图上,量得甲、乙两地间的距离为3.6厘米。如果王叔叔开车从甲地出发以每小时60千米的速度行驶,几小时可以到达乙地?
过程讲解
已知图上距离和比例尺,根据“实际距离=图上距离÷比例尺”求出实际距离,即甲、乙两地间的路程。再根据“路程÷速度=时间”,求出王叔叔需要行驶的时间。
解答:3.6÷ =3.6×5000000=18000000(厘米)
18000000 厘米=180千米
180÷60=3(小时)
答:3 小时可以到达乙地。
实战演练 3
在一幅地图上,用3厘米的线段表示实际距离900千米。
(1)这幅地图的比例尺是多少?
1∶30000000
(2)一条长480千米的高速公路,在这幅地图上是多少厘米?
1.6厘米
1. 按一定的比分配问题。
(1)按一定的比分配的应用题:把一个数量按照一定的比分配成几部分,求每部分数量各是多少的应用题。
(2)解题方法。
一般方法:把比转化成分数,用分数方法解答,即先求总份数,再求各部分占总量的几分之几,最后按求一个数的几分之几是多少,用乘法计算,求出各部分的量是多少。
归一法:把比看作分得的份数,先求出总份数,然后用“总量÷总份数=平均每份的量”求出每份的量,再用“每份的量×各部分量所对应的份数”求出各部分的量。
用比例知识解答:首先设未知量为x,根据题中“已知比等于相对应的量的比”作为等量关系式,列出含有 x的比例式,再解比例求出x。
2. 用正、反比例知识解答应用题的步骤。
(1)分析数量关系。判断成什么比例。
(2)找等量关系。如果是成正比例,则按“等比”找等量关系式;如果是成反比例,则按“等积”找等量关系式。
(3)列比例式。设未知数为 x,根据等量关系式列出正比例式或反比例式。
(4)解比例。
(5)检验并写答语。
例 1 美术小组一共有45人,其中男生和女生的人数比为2∶3。美术小组男生和女生各有多少人?
过程讲解
我们可以这样想,男生和女生的人数比为2∶3,可以把男生人数看作2份,女生人数看作3份,美术小组总人数对应的总份数就是2+3=5(份),我们可以求出每份的人数为45÷5=9(人),男生有9×2=18(人),女生有9×3=27(人)。
我们也可以利用分数的相关知识来解决,因为男生和女生的人数比2∶3,所以男生占总人数的
女生占总人数的 根据分数乘法的意义,男生的人数为45× =18(人),女生的人数为45×
=27(人)。
解答:方法一 2+3=5(份) 45÷5=9(人)
男生:9×2=18(人)
女生:9×3=27(人)
方法二 男生:45× =18(人)
女生:45× =27(人)
答:美术小组男生有 18 人,女生有 27 人。
例 2 修路队修一条公路,原计划每天修1200米,50天可以修完。实际每天修2400米,实际需要多少天完成?
过程讲解
这道题中,每天修的米数和修的天数是两种相关联的量,因为“每天修的米数×修的天数=路的长度”,而路的长度一定,所以每天修的米数和修的天数成反比例关系,因此,我们可以根据反比例的意义列出等式并解答。
解答:解:设实际需要x天完成。
2400x=1200×50
2400x=60000
x=25
答:实际需要25天完成。
例 3 某修路队要修一段长28.8千米的公路,前4天修了7.2千米,照这样计算,剩下的还要多少天修完?(用比例解)
过程讲解
“照这样计算”就是说每天修路的长度是一定的,所以修路长度和修路天数成正比例关系。因此,我们可以根据正比例的意义列出等式并解答。
解答:解:设剩下的还要x天修完。
7.2x=4×(28.8-7.2)
7.2x=86.4
x=12
答:剩下的还要12天修完。
实战演练 4
1. 一种灭蝇药,用药液和水按1∶1500配制而成,要配制这种药水750.5千克,需要药液与水各多少千克?
需要药液0.5kg,水750kg。
2. 测量小组要测量一棵树的高度。量得树的影长是8.4米,同一时间量得附近一根2米长的直立竹竿的影长是1.2米。这棵树的高度是多少米?
14米
3. 装修一间客厅,用边长5dm的方砖铺地,需要 80块,如果改用边长4dm的方砖铺地,需要多少块?
(用比例解)
125块
4. 某售楼处销售一处新建楼房,计划每天销售30 套,12天售完。实际平均每天多售6套,实际比计划少
用多少天售完全部楼房?
2天
