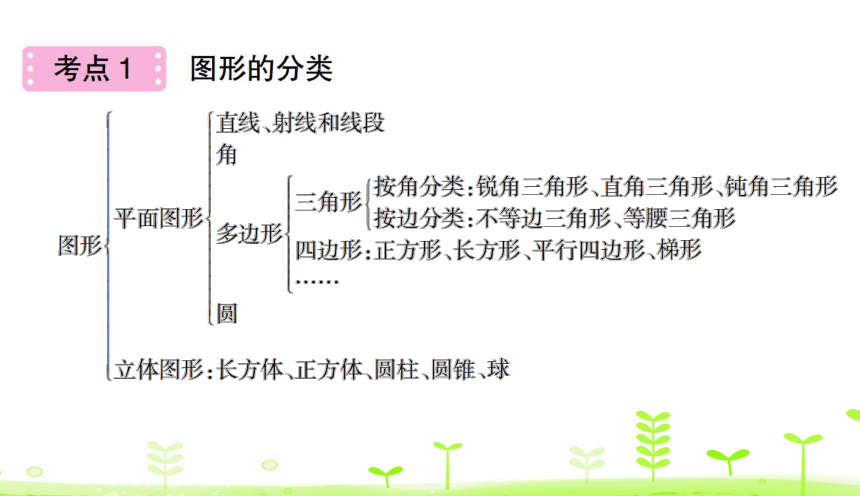
人教版数学六年级下册期末复习课件-6.2.1 图形的认识与测量(一)平面图形 课件(68张PPT)
文档属性
| 名称 | 人教版数学六年级下册期末复习课件-6.2.1 图形的认识与测量(一)平面图形 课件(68张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览







文档简介
(共68张PPT)
6.2.1 图形的认识与
测量(一)平面图形
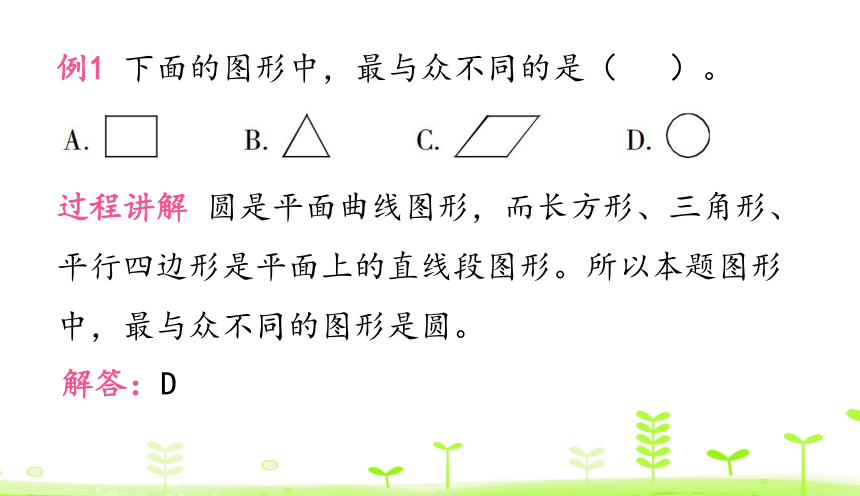
例1 下面的图形中,最与众不同的是( )。
过程讲解 圆是平面曲线图形,而长方形、三角形、平行四边形是平面上的直线段图形。所以本题图形中,最与众不同的图形是圆。
解答:D
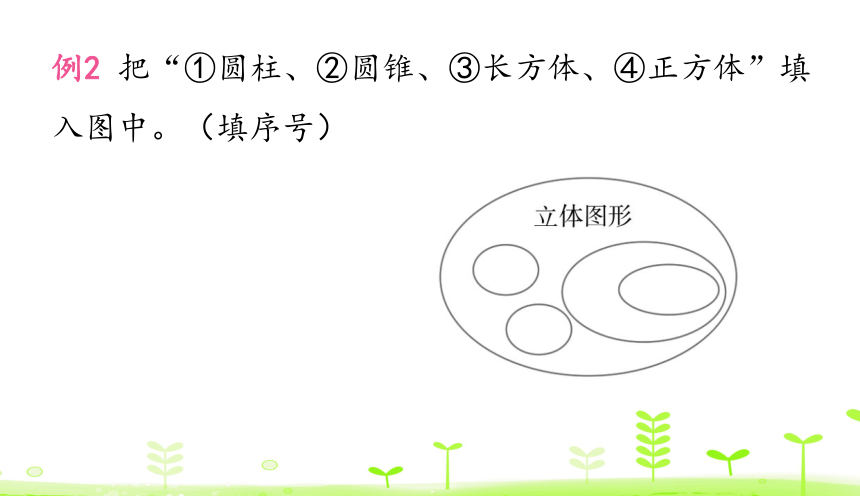
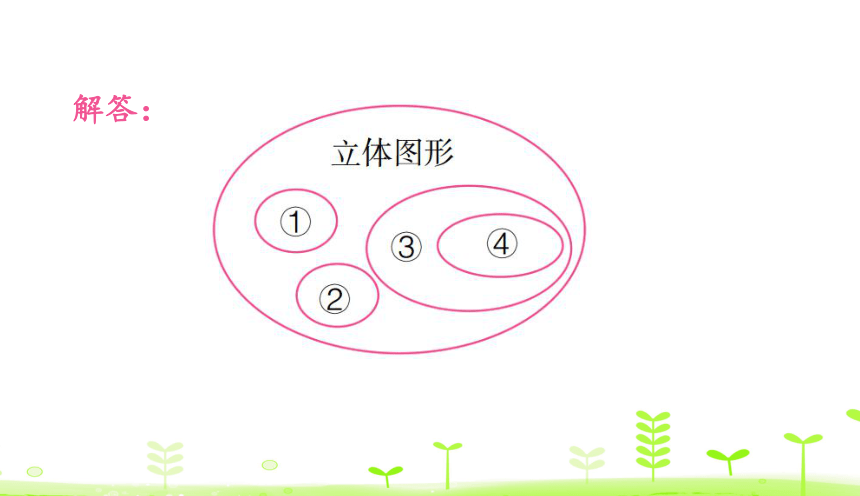
例2 把“①圆柱、②圆锥、③长方体、④正方体”填入图中。(填序号)
过程讲解 我们学过的立体图形有圆柱、圆锥、长方体、正方体等,其中正方体是长、宽、高都相等的长方体,是长方体的一种特殊情况,由此即可解答此题。
解答:
实战演练 1
1. 填空题。
(1)我们学过的图形主要分为( )图形和( )图形。
(2)我们学过的平面图形有( )、( )、( )、( )、( )和( );立体图形有( )、( )、( )、( )和( )。
平面
立体
长方形
正方形
平行四边形
三角形
梯形
圆
长方体
正方体
球
圆柱
圆锥
2. 选择题。
(1)从圆柱的上面看,看到的形状是( )。
A.正方形 B.长方形 C. 圆
(2)下列立体图形,截面形状不可能是长方形的
是( )。
C
C
点与直线:过一点可以画无数条直线。两点确定一条直线。
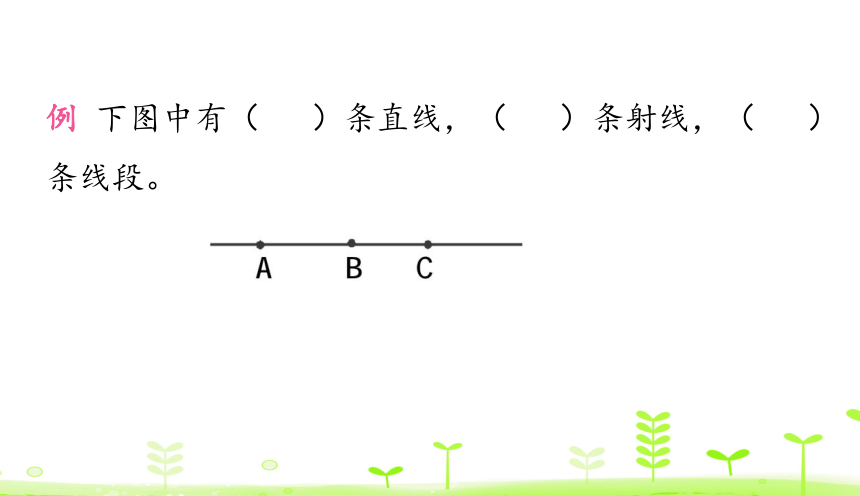
例 下图中有( )条直线,( )条射线,( )条线段。
过程讲解 此题是对直线、射线、线段等知识的考查。
直线:1条。
射线:以A、B、C 为端点的射线各有两条,共有6条。
线段:以A为左端点的线段有2条,如左下图;以B为左端点的线段有1条,如右下图。共有3条线段。
在一条直线上有n个点,则共有2n条射线,有
条线段。
解答:1 6 3
实战演练 2
1. 画一条长 5 厘米的( )。
A.直线 B.线段 C.射线
2. 判断题。(对的打“√”,错的打“×”)
(1)直线比射线长,射线比线段长。 ( )
B
×
(2)把线段一端延长,可得到一条直线。 ( )
(3)过一点可以画无数条直线,过两点只能画一
条线段。 ( )
(4)线段有两个端点,直线没有端点。 ( )
×
√
√
平行:同一平面内,不相交的两条直线互相平行。
垂直:两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
点到直线的距离:从直线外一点到这条直线所画的垂直线段的长,叫做这个点到直线的距离。
同一平面内的两条直线不是平行,就是相交,垂直是相交的特例。
例 如图,过点P画出已知直线l的垂线和平行线,并量出图中点P到直线l的距离。
过程讲解 此题是对垂线、平行线、点到直线的距离等知识及动手操作能力的考查。画图时先用三角板的一条直角边与直线对齐,使另一条直角边在点P的一边,再沿着直线平移三角板,使另一条直角边正好通过点P,并沿着这条直角边画出已知直线的垂线。垂足为D,并量出PD的长度。
画平行线时将一把三角板的一条直角边与直线重合,另一把三角板的一条直角边与第一把三角板的另一条直角边靠在一起,平移另一把三角板的一条直角边,直至这条直角边通过点P,再沿着这条直角边画出已知直线的平行线。
解答:
量出点P到直线l的距离是1cm。
实战演练 3
1. 判断题。(对的打“√”,错的打“×”)
(1)两条平行线之间可以画无数条垂直线段,这些
垂直线段长度相等。 ( )
√
(2)不相交的两条直线叫做平行线。 ( )
(3)两条直线分别与第三条直线平行,则这三条直
线都互相平行。 ( )
×
√
2. 如图,过点 A 画已知直线的平行线和垂线。
请同学们自己做一做。
1. 角的意义。
从一点引出的两条射线所组成的图形叫做角。角的大小与两边的长短无关,与两边张开的大小有关。在放大镜下看角,角的两边变长了,但角的大小没变。
2. 角的分类。
例 指出下图钟面上的时针和分针分别组成什么角?
过程讲解 根据角分类的范围:大于0°且小于90°的角是锐角;90°的角是直角;大于90°且小于180°的角是钝角;等于180°的角是平角。第一幅图时针和分针组成的角是60°,第二幅图时针和分针组成的角是90°,第三幅图时针和分针组成的角是120°。
解答:锐角 直角 钝角
实战演练 4
1. 填空题。
(1)从一点引出两条射线所组成的图形叫做( )。
(2)角的大小与( )无关,与( )有关。
角
两边的长短
两边张开的大小
2. 在可以放大4倍的放大镜下看50°的角,你看到的角的度数是( )。
A. 50° B. 100° C. 200°
A
1. 三角形的意义:由三条线段首尾顺次连接围成一个封闭的平面图形。
2. 三角形各部分的名称:围成三角形的三条线段叫做三角形的边;每两条边的交点叫做三角形的顶点;每两条边所形成的角叫做三角形的内角。一个三角形有三条边,三个顶点和三个内角。
从三角形的一个顶点向它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。
3. 三角形的特点和特性:三角形具有稳定性;三角形任意两边之和大于第三边;三角形的内角和是180°。
4. 三角形分类。
例 如图,在三角形ABC中,AB=AC,∠C=40°。在BC边上取一点D,已知∠ADC=70°,求∠BAD的度数。
过程讲解 此题是对三角形内角和、等腰三角形的特点、平角等知识的考查。由AB=AC得∠B=∠C=40°。由∠BDC 是平角可求得∠ADB的度数。在三角形ABD中,由三角形内角和为180°得∠BAD=180°-∠B-∠ADB,由此可求出∠BAD的度数。
解答:因为 AB=AC,所以∠B=∠C=40°。
∠ADB=180°-70°=110°
∠BAD=180°-40°-110°=30°
答:∠BAD 的度数是30°。
实战演练 5
1. 填空题。
(1)一个三角形中,最大的角是75°,这个三角形
是( )三角形。
(2)一个等腰三角形的顶角是80°,那么这个等
腰三角形的一个底角是( )。
锐角
50°
2. 下面的线段中,可以围成三角形的一组是( )。
A. 2cm、3cm、7cm
B. 2cm、5cm、7cm
C. 2cm、6cm、7cm
C
1. 四边形的意义:在同一平面内,由四条线段首尾顺次相接,围成的一个封闭的图形叫做四边形。
2. 不同四边形之间的关系。
3. 四边形的特征。
4. 四边形的特性:四边形不稳定,容易变形。四边形的内角和是360°。
例 数一数,右图中有多少个长方形?有多少个三角形?有多少个梯形?
过程讲解 此题是对各种平面图形的特征的考查。线段 BD上有6条线段,可分别作为长方形的长,线段AB上有3条线段,可分别作为长方形的宽,所以共有长方形 6×3=18(个)。
以A为顶点的三角形有4个,以G为顶点但不以A为顶点的三角形有6个,以F为顶点但不以A、G为顶点的三角形有5个,以D为顶点但不以G、F为顶点的三角形有1个,所以共有三角形4+6+5+1=16(个)。
在AC和HI这两条平行线之间有10个梯形,在HI和BD这两条平行线之间有10个梯形,在AC和BD这两条平行线之间有6个梯形,所以共有梯形10+10+6=26(个)。
解答:图中有18个长方形,有16个三角形,有26个梯形。
实战演练 6
1. 填空题。
(1)一个正方形有( )条对称轴,平行四边形
( )轴对称图形。(后一空填“是”或“不
是”)
(2)两个不完全相同的梯形( )拼成一个长方
形。(填“可以”或“不可以”)
4
不是
可以
2. 下面是用木条钉成的支架,其中最不容易变形的
是( )。
D
1. 圆的意义:圆是平面上一种封闭的曲线图形。
2. 圆各部分的名称:圆中心的一点叫做圆心,一般用字母O表示;圆心到圆上任意一点的线段叫做半径,半径决定圆的大小,一般用字母r表示;通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示。
3. 半径与直径的关系:在同一圆内,所有的半径都相等,所有的直径也都相等。直径等于半径的2倍,半径是直径的 即 d=2r,r=
4. 圆的轴对称性:圆的直径所在的直线都是它的对称轴,圆有无数条对称轴。
5. 圆环:两个半径不相等的同心圆之间的部分叫做圆环。如图(阴影部分): 。
6. 扇形:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
例 同学们进行套圈游戏,下面哪一种站法最公平?
过程讲解 要判断哪一种站法最公平,我们就看每个同学所站的位置与套圈目标的距离是否相等。如果距离都相等,表示公平;如果距离不相等,表示不公平。而上面的第三种站法,同学们都站在圆的边上,每个人到圆心的距离都是半径的长度,都相等,因此第三种站法最公平。
解答:第三种站法最公平。
实战演练 7
1. 圆内最长的线段是( ),圆有( )条对称轴。
2. 同圆或等圆中,所有的直径都( ),所有的半径都( );直径是半径的( )倍,半径是直径的( )。
直径
无数
相等
相等
2
2
1
3. 我们用圆规画一个直径为6cm的圆,圆规两脚之间的距离应取( )厘米。
A. 1.5 B. 3 C. 6 D. 12
B
例1 下图中大正方形的边长是8厘米,小正方形的边长是6厘米,求阴影部分的面积。
过程讲解 此题是对三角形面积公式应用的考查。因为图中阴影部分是一个三角形,这个三角形的底是大正方形边长与小正方形边长的差,即8-6=2(cm),高在三角形外,正好是大正方形的边长8cm。
解答:(8-6)×8÷2=8(cm )
答:阴影部分的面积是8平方厘米。
例2 如下图,小明和爸爸在自家墙外围了一个养鸡场,
养鸡场的篱笆总长是30m,其中不靠墙的一条边长是 8m,求养鸡场的面积。
过程讲解 围成的养鸡场是个直角梯形,所给的不靠墙的一条边是这个梯形的高,由题目中提供的信息可以先求出上底与下底的和,再根据梯形的面积计算公式求出养鸡场的面积。
解答:(30-8)×8÷2=88(m )
答:养鸡场的面积是88平方米。
例3 求图中阴影部分的面积。(单位:cm)
过程讲解 此题是求组合图形的面积,考查的是应用面积公式解决实际问题的能力。这个图形中有圆、三角形、梯形、半圆等图形,计算前要先对图形进行分析,看阴影部分的面积是哪些图形的面积和或差。
解答:方法一 阴影面积=半圆面积-三角形面积+梯形面积-半圆面积
方法二 将阴影部分割补成图1或图2,使计算简化。
(2×2+6)×2÷2-2×2×2÷2=10-4=6(cm )
或[2+(6-2)]×2÷2=6×2÷2=6(cm )
答:阴影部分的面积是 6cm 。
实战演练 8
1. 填空题。
(1)一个三角形的面积是6cm ,和它等底等高的平
行四边形的面积是( )。
(2)把一个周长是16cm的正方形剪成一个最大的圆,
这个圆的面积是( ),周长是( )。
12cm
12.56cm
12.56cm
(3)下图中有( )个三角形的面积与阴影部分面积相等,面积是( )。
(4)把一个圆平均分成若干个小扇形后,拼成一个
近似的长方形,周长比原来增加了8cm,这个圆的面积是( )cm 。
2
24cm
50.24
2. 一块正方形菜地,一边靠墙,其余三边围上总长度为27米的竹篱笆,这块正方形菜地的面积是多少平方米?
27÷3=9(米)
9×9=81(平方米)
答:这块正方形菜地的面积是81平方米。
3. 一个梯形,上底是12cm,下底是15cm,高是8cm,它的面积是多少平方厘米?
(12+15)×8÷2=108(cm )
答:它的面积是108平方厘米。
4. 如下图,圆形花坛的半径是8m,在花坛的周围修一条2m宽的水泥路。求水泥路的面积。
3.14×(8+2) -3.14×8 =113.04(m )
答:水泥路面积是113.04m 。
6.2.1 图形的认识与
测量(一)平面图形
例1 下面的图形中,最与众不同的是( )。
过程讲解 圆是平面曲线图形,而长方形、三角形、平行四边形是平面上的直线段图形。所以本题图形中,最与众不同的图形是圆。
解答:D
例2 把“①圆柱、②圆锥、③长方体、④正方体”填入图中。(填序号)
过程讲解 我们学过的立体图形有圆柱、圆锥、长方体、正方体等,其中正方体是长、宽、高都相等的长方体,是长方体的一种特殊情况,由此即可解答此题。
解答:
实战演练 1
1. 填空题。
(1)我们学过的图形主要分为( )图形和( )图形。
(2)我们学过的平面图形有( )、( )、( )、( )、( )和( );立体图形有( )、( )、( )、( )和( )。
平面
立体
长方形
正方形
平行四边形
三角形
梯形
圆
长方体
正方体
球
圆柱
圆锥
2. 选择题。
(1)从圆柱的上面看,看到的形状是( )。
A.正方形 B.长方形 C. 圆
(2)下列立体图形,截面形状不可能是长方形的
是( )。
C
C
点与直线:过一点可以画无数条直线。两点确定一条直线。
例 下图中有( )条直线,( )条射线,( )条线段。
过程讲解 此题是对直线、射线、线段等知识的考查。
直线:1条。
射线:以A、B、C 为端点的射线各有两条,共有6条。
线段:以A为左端点的线段有2条,如左下图;以B为左端点的线段有1条,如右下图。共有3条线段。
在一条直线上有n个点,则共有2n条射线,有
条线段。
解答:1 6 3
实战演练 2
1. 画一条长 5 厘米的( )。
A.直线 B.线段 C.射线
2. 判断题。(对的打“√”,错的打“×”)
(1)直线比射线长,射线比线段长。 ( )
B
×
(2)把线段一端延长,可得到一条直线。 ( )
(3)过一点可以画无数条直线,过两点只能画一
条线段。 ( )
(4)线段有两个端点,直线没有端点。 ( )
×
√
√
平行:同一平面内,不相交的两条直线互相平行。
垂直:两条直线相交成直角时,这两条直线互相垂直。其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
点到直线的距离:从直线外一点到这条直线所画的垂直线段的长,叫做这个点到直线的距离。
同一平面内的两条直线不是平行,就是相交,垂直是相交的特例。
例 如图,过点P画出已知直线l的垂线和平行线,并量出图中点P到直线l的距离。
过程讲解 此题是对垂线、平行线、点到直线的距离等知识及动手操作能力的考查。画图时先用三角板的一条直角边与直线对齐,使另一条直角边在点P的一边,再沿着直线平移三角板,使另一条直角边正好通过点P,并沿着这条直角边画出已知直线的垂线。垂足为D,并量出PD的长度。
画平行线时将一把三角板的一条直角边与直线重合,另一把三角板的一条直角边与第一把三角板的另一条直角边靠在一起,平移另一把三角板的一条直角边,直至这条直角边通过点P,再沿着这条直角边画出已知直线的平行线。
解答:
量出点P到直线l的距离是1cm。
实战演练 3
1. 判断题。(对的打“√”,错的打“×”)
(1)两条平行线之间可以画无数条垂直线段,这些
垂直线段长度相等。 ( )
√
(2)不相交的两条直线叫做平行线。 ( )
(3)两条直线分别与第三条直线平行,则这三条直
线都互相平行。 ( )
×
√
2. 如图,过点 A 画已知直线的平行线和垂线。
请同学们自己做一做。
1. 角的意义。
从一点引出的两条射线所组成的图形叫做角。角的大小与两边的长短无关,与两边张开的大小有关。在放大镜下看角,角的两边变长了,但角的大小没变。
2. 角的分类。
例 指出下图钟面上的时针和分针分别组成什么角?
过程讲解 根据角分类的范围:大于0°且小于90°的角是锐角;90°的角是直角;大于90°且小于180°的角是钝角;等于180°的角是平角。第一幅图时针和分针组成的角是60°,第二幅图时针和分针组成的角是90°,第三幅图时针和分针组成的角是120°。
解答:锐角 直角 钝角
实战演练 4
1. 填空题。
(1)从一点引出两条射线所组成的图形叫做( )。
(2)角的大小与( )无关,与( )有关。
角
两边的长短
两边张开的大小
2. 在可以放大4倍的放大镜下看50°的角,你看到的角的度数是( )。
A. 50° B. 100° C. 200°
A
1. 三角形的意义:由三条线段首尾顺次连接围成一个封闭的平面图形。
2. 三角形各部分的名称:围成三角形的三条线段叫做三角形的边;每两条边的交点叫做三角形的顶点;每两条边所形成的角叫做三角形的内角。一个三角形有三条边,三个顶点和三个内角。
从三角形的一个顶点向它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高。
3. 三角形的特点和特性:三角形具有稳定性;三角形任意两边之和大于第三边;三角形的内角和是180°。
4. 三角形分类。
例 如图,在三角形ABC中,AB=AC,∠C=40°。在BC边上取一点D,已知∠ADC=70°,求∠BAD的度数。
过程讲解 此题是对三角形内角和、等腰三角形的特点、平角等知识的考查。由AB=AC得∠B=∠C=40°。由∠BDC 是平角可求得∠ADB的度数。在三角形ABD中,由三角形内角和为180°得∠BAD=180°-∠B-∠ADB,由此可求出∠BAD的度数。
解答:因为 AB=AC,所以∠B=∠C=40°。
∠ADB=180°-70°=110°
∠BAD=180°-40°-110°=30°
答:∠BAD 的度数是30°。
实战演练 5
1. 填空题。
(1)一个三角形中,最大的角是75°,这个三角形
是( )三角形。
(2)一个等腰三角形的顶角是80°,那么这个等
腰三角形的一个底角是( )。
锐角
50°
2. 下面的线段中,可以围成三角形的一组是( )。
A. 2cm、3cm、7cm
B. 2cm、5cm、7cm
C. 2cm、6cm、7cm
C
1. 四边形的意义:在同一平面内,由四条线段首尾顺次相接,围成的一个封闭的图形叫做四边形。
2. 不同四边形之间的关系。
3. 四边形的特征。
4. 四边形的特性:四边形不稳定,容易变形。四边形的内角和是360°。
例 数一数,右图中有多少个长方形?有多少个三角形?有多少个梯形?
过程讲解 此题是对各种平面图形的特征的考查。线段 BD上有6条线段,可分别作为长方形的长,线段AB上有3条线段,可分别作为长方形的宽,所以共有长方形 6×3=18(个)。
以A为顶点的三角形有4个,以G为顶点但不以A为顶点的三角形有6个,以F为顶点但不以A、G为顶点的三角形有5个,以D为顶点但不以G、F为顶点的三角形有1个,所以共有三角形4+6+5+1=16(个)。
在AC和HI这两条平行线之间有10个梯形,在HI和BD这两条平行线之间有10个梯形,在AC和BD这两条平行线之间有6个梯形,所以共有梯形10+10+6=26(个)。
解答:图中有18个长方形,有16个三角形,有26个梯形。
实战演练 6
1. 填空题。
(1)一个正方形有( )条对称轴,平行四边形
( )轴对称图形。(后一空填“是”或“不
是”)
(2)两个不完全相同的梯形( )拼成一个长方
形。(填“可以”或“不可以”)
4
不是
可以
2. 下面是用木条钉成的支架,其中最不容易变形的
是( )。
D
1. 圆的意义:圆是平面上一种封闭的曲线图形。
2. 圆各部分的名称:圆中心的一点叫做圆心,一般用字母O表示;圆心到圆上任意一点的线段叫做半径,半径决定圆的大小,一般用字母r表示;通过圆心并且两端都在圆上的线段叫做直径,一般用字母d表示。
3. 半径与直径的关系:在同一圆内,所有的半径都相等,所有的直径也都相等。直径等于半径的2倍,半径是直径的 即 d=2r,r=
4. 圆的轴对称性:圆的直径所在的直线都是它的对称轴,圆有无数条对称轴。
5. 圆环:两个半径不相等的同心圆之间的部分叫做圆环。如图(阴影部分): 。
6. 扇形:一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
例 同学们进行套圈游戏,下面哪一种站法最公平?
过程讲解 要判断哪一种站法最公平,我们就看每个同学所站的位置与套圈目标的距离是否相等。如果距离都相等,表示公平;如果距离不相等,表示不公平。而上面的第三种站法,同学们都站在圆的边上,每个人到圆心的距离都是半径的长度,都相等,因此第三种站法最公平。
解答:第三种站法最公平。
实战演练 7
1. 圆内最长的线段是( ),圆有( )条对称轴。
2. 同圆或等圆中,所有的直径都( ),所有的半径都( );直径是半径的( )倍,半径是直径的( )。
直径
无数
相等
相等
2
2
1
3. 我们用圆规画一个直径为6cm的圆,圆规两脚之间的距离应取( )厘米。
A. 1.5 B. 3 C. 6 D. 12
B
例1 下图中大正方形的边长是8厘米,小正方形的边长是6厘米,求阴影部分的面积。
过程讲解 此题是对三角形面积公式应用的考查。因为图中阴影部分是一个三角形,这个三角形的底是大正方形边长与小正方形边长的差,即8-6=2(cm),高在三角形外,正好是大正方形的边长8cm。
解答:(8-6)×8÷2=8(cm )
答:阴影部分的面积是8平方厘米。
例2 如下图,小明和爸爸在自家墙外围了一个养鸡场,
养鸡场的篱笆总长是30m,其中不靠墙的一条边长是 8m,求养鸡场的面积。
过程讲解 围成的养鸡场是个直角梯形,所给的不靠墙的一条边是这个梯形的高,由题目中提供的信息可以先求出上底与下底的和,再根据梯形的面积计算公式求出养鸡场的面积。
解答:(30-8)×8÷2=88(m )
答:养鸡场的面积是88平方米。
例3 求图中阴影部分的面积。(单位:cm)
过程讲解 此题是求组合图形的面积,考查的是应用面积公式解决实际问题的能力。这个图形中有圆、三角形、梯形、半圆等图形,计算前要先对图形进行分析,看阴影部分的面积是哪些图形的面积和或差。
解答:方法一 阴影面积=半圆面积-三角形面积+梯形面积-半圆面积
方法二 将阴影部分割补成图1或图2,使计算简化。
(2×2+6)×2÷2-2×2×2÷2=10-4=6(cm )
或[2+(6-2)]×2÷2=6×2÷2=6(cm )
答:阴影部分的面积是 6cm 。
实战演练 8
1. 填空题。
(1)一个三角形的面积是6cm ,和它等底等高的平
行四边形的面积是( )。
(2)把一个周长是16cm的正方形剪成一个最大的圆,
这个圆的面积是( ),周长是( )。
12cm
12.56cm
12.56cm
(3)下图中有( )个三角形的面积与阴影部分面积相等,面积是( )。
(4)把一个圆平均分成若干个小扇形后,拼成一个
近似的长方形,周长比原来增加了8cm,这个圆的面积是( )cm 。
2
24cm
50.24
2. 一块正方形菜地,一边靠墙,其余三边围上总长度为27米的竹篱笆,这块正方形菜地的面积是多少平方米?
27÷3=9(米)
9×9=81(平方米)
答:这块正方形菜地的面积是81平方米。
3. 一个梯形,上底是12cm,下底是15cm,高是8cm,它的面积是多少平方厘米?
(12+15)×8÷2=108(cm )
答:它的面积是108平方厘米。
4. 如下图,圆形花坛的半径是8m,在花坛的周围修一条2m宽的水泥路。求水泥路的面积。
3.14×(8+2) -3.14×8 =113.04(m )
答:水泥路面积是113.04m 。
