人教版数学六年级下册期末复习课件-6.3 统计与概率 课件(39张PPT)
文档属性
| 名称 | 人教版数学六年级下册期末复习课件-6.3 统计与概率 课件(39张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 18:26:10 | ||
图片预览








文档简介
(共39张PPT)
6.3.3 统计与概率
(1)确定调查对象。(2)确定调查内容。(3)确定调查方式。(4)呈现调查数据。(5)分析调查数据,解决问题。
1. 设计统计表的方法及步骤。
(1)收集数据,整理数据。
(2)根据资料和制表要求确定统计表的格式和项目。
(3)根据整理好的数据填表。
(4)填写总计与合计。
(5)注明统计表的名称、数量单位和制表日期。
2. 设计统计表。
逐项数出各个类别的数目,用画“正”字等方法整理。把收集的数据整理以后制成表格,用来反映情况,分析具体问题,这样的表格叫做统计表。统计表主要分为单式统计表和复式统计表。单式统计表只有一个统计项目,而复式统计表含有两个或两个以上统计项目。
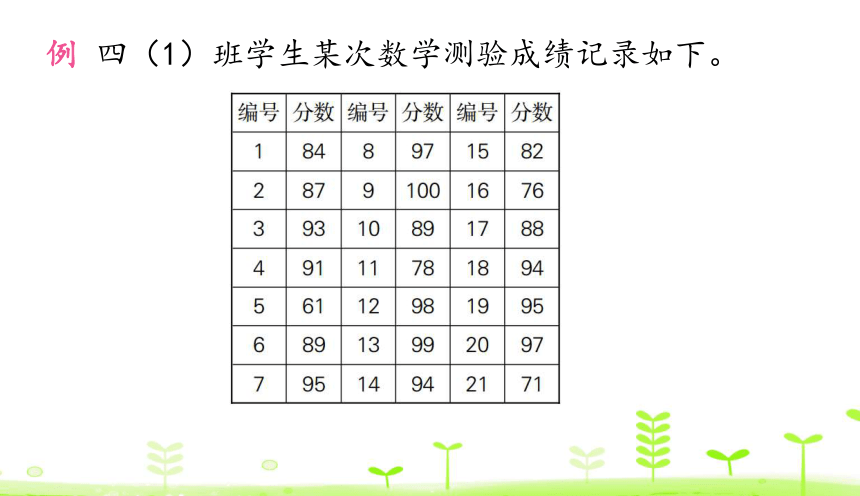
例 四(1)班学生某次数学测验成绩记录如下。
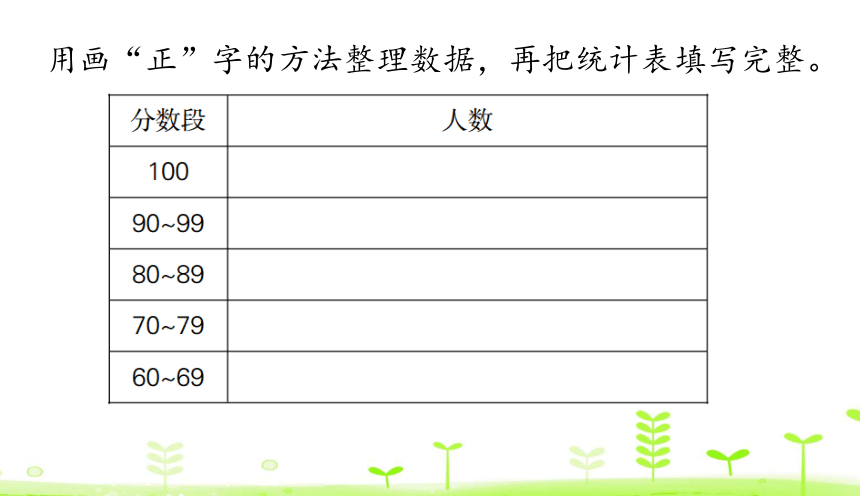
用画“正”字的方法整理数据,再把统计表填写完整。
四(1)班学生某次数学测验成绩统计表
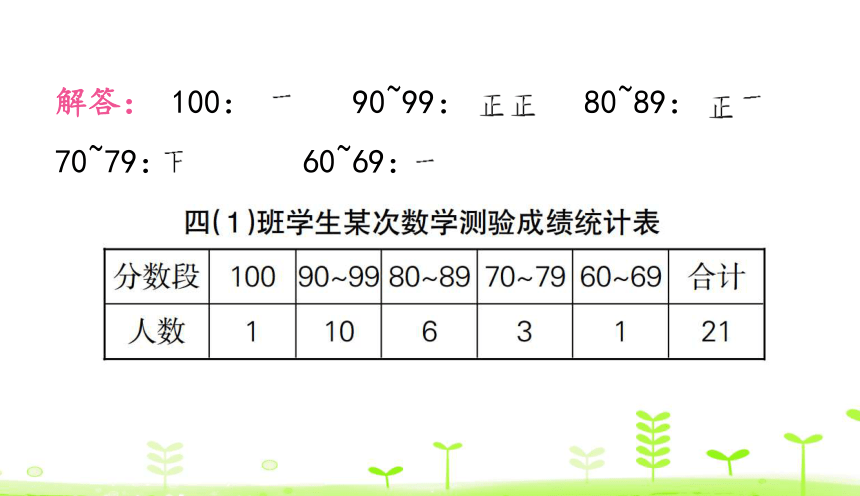
过程讲解 这是一道将四(1)班学生某次数学测验成绩进行整理,并制作统计表的题目。首先,可按照统计表中划分的分数段,对原始数据进行整理,在统计时要注意有序,做到不重复、不遗漏。“正”字中的每一笔画表示1人,1个“正”字表示5人。在制作统计表时,其中的“合计”表示将各个分数段的人数加起来,得出的合计人数应该和原始数据中的总人数相等。
解答: 100: 90~99: 80~89: 70~79: 60~69:
实战演练 1
五(1)班全体同学的左眼视力情况如下。
5.0 4.9 5.3 5.2 4.7 5.2
4.8 5.1 5.3 5.2 4.8 5.0
4.5 5.1 4.9 5.1 4.7 5.0
4.8 5.1 5.0 4.8 4.9 5.1
4.5 5.1 4.6 5.1 4.7 5.1
5.0 5.1 5.1 4.9 5.0 5.1
5.2 5.1 4.6 5.0 4.7 4.6
5.2 5.0 4.9 4.7 5.2 4.8
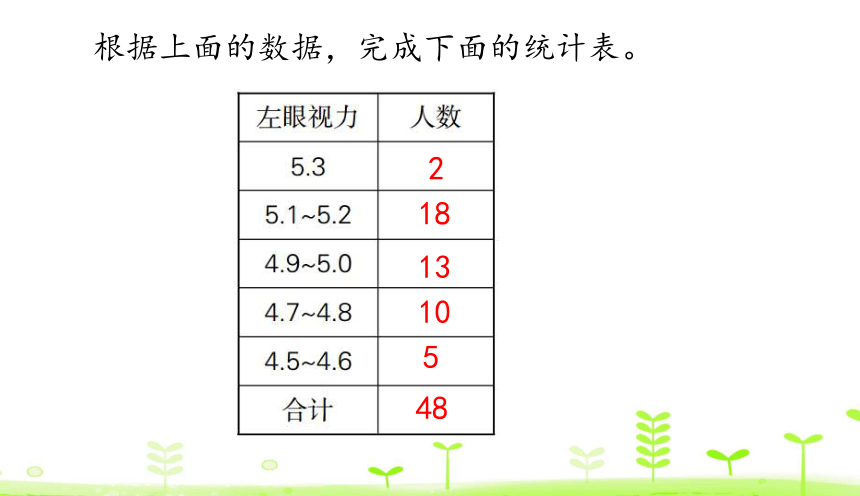
根据上面的数据,完成下面的统计表。
2
18
13
10
5
48
1. 条形统计图、折线统计图、扇形统计图的特点及作用。
2. 绘制统计图。
(1)绘制条形统计图的步骤和方法。
①画出两条互相垂直的射线;②在一条射线上适当分配条形的位置,确定直条的宽度和间隔;③在另一条射线上根据数据的大小,确定单位长度表示多少;④按照数据的多少画出长短不同的直条,并注明数量。
(2)绘制折线统计图的步骤和方法。
①画出两条互相垂直的射线;②在水平射线上适当分配折线的位置,确定折线的间隔;③在垂直射线上根据数据的大小,确定单位长度表示多少;④按照数据的大小先描出各点,再用线段顺次连接起来,并注明数量。
(3)绘制扇形统计图的步骤和方法。
①计算各部分数量占总量的百分之几;②计算表示各部分数量对应的扇形的圆心角度数;③画一个适当大小的圆,并按照上面所得的圆心角度数,在圆里画出各个扇形;④在每个扇形中标明所表示的各部分数量的名称及所占的百分数,并把各个扇形涂上不同的颜色或条纹加
以区分。
3. 分析统计图:会根据统计图进行数据分析,提出问题,并能作出简单的判断和预测。
例 (教材第 97 页)六(1)班同学的几项数据用统计表和统计图表示如下。
(1)根据以上统计图表,你得到了哪些信息?
(2)除了通过问卷调查收集数据外,还可以通过什么手段收集数据?
过程讲解 此题是对统计图、表特征掌握情况的考查。要根据各统计图、表的特征及所反映的相关数据来回答问题。不仅要发现一些表面的数据,而且还要从数据中发现更深层次的信息。
解答:(1)①从统计表中可以看出六(1)班有男生 22人,女生18人,全班总人数为40人。
②从扇形统计图中可以知道六(1)班男生人数占全班人数的55%,女生人数占全班人数的45%。
③条形统计图表示六(1)班男生和女生最喜欢的运动项目的人数,其中喜欢足球的男生人数比女生多,喜欢跳绳的女生人数比男生多,喜欢乒乓球的男生人数和女生同样多……
(2)还可以通过采访、收集各种媒体信息等方法收集数据。
实战演练 2
阅读下面的统计图,并回答问题。
某城市人均绿地面积变化情况统计图
(2012年~2016年)
(1)2013年该城市人均绿地面积比2012年增加了
多少平方米?增加了百分之几?(百分号前保留一
位小数)
0.4平方米
4.3%
(2)2015年该城市人均绿地面积比2016年少多少平方米?少百分之几?(百分号前保留一位小数)
0.4平方米
3.5%
1. 统计量的意义、作用和求法。
2. 可能性。
(1)生活中,有些事件的发生是不确定的,一般用“可能发生”来描述;有些事件的发生是确定的,一般用“一定发生”或“不可能发生”来描述。
(2)某些事情发生的可能性有大有小,当事件发生的可能性的大小与物体数量相关时,在总数或总体中物体数量越多,出现对应结果的可能性越大;物体数量越少,出现对应结果的可能性就越小。
3. 游戏规则的公平性。
根据事情发生的可能性大小设计游戏规则:当游戏双方机会均等时,游戏规则公平;当游戏双方机会不均等时,游戏规则不公平。
例 (教材第 97 页)六(1)班同学身高、体重情况如下表。
(1)上面两组数据的平均数各是多少?
(2)小组讨论,什么数据能代表全班同学的身高和体重?
(3)如果把全班同学编号,随意抽取一名学生,该生体重在36kg及以下的可能性大?还是在39kg及以上的可能性大?
过程讲解 平均数等于身高(体重)总和除以总人数;在这两组数据中,最大数据与最小数据相差不大,故用平均数可以反映这两组数据的一般水平;把全班同学编号,随意抽取一名学生,体重在36kg及以下的人数是11人,39kg及以上的人数是29人,29>11,所以体重在39kg及以上的可能性大。
解答:(1)第一组数据的平均数:(1.40×1+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3)÷(1+3+5+10+12+6+3)=60.17÷40≈1.50(m)
第二组数据的平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3)÷(2+4+5+12+10+4+3)=1584÷40=39.6(kg)
(2)平均数能代表全班同学的身高和体重。
(3)把全班同学编号,随意抽取一名学生,该生体重在39kg 及以上的可能性大。
实战演练 3
下面是某商场2017年7月电冰箱的销售情况统计表。
(1)这组数据的平均数、中位数和众数各是多少?
(除不尽的保留一位小数)
10.5 10 10
(2)你认为用哪一个数据来表示销售员的销售水平比较合适呢?
用中位数10或众数10表示比较合适。
(3)如果把销售员编号,随意抽取一位,该销售员
销售台数在10台的可能性大还是12台的可能性大?
10 台的可能性大。
6.3.3 统计与概率
(1)确定调查对象。(2)确定调查内容。(3)确定调查方式。(4)呈现调查数据。(5)分析调查数据,解决问题。
1. 设计统计表的方法及步骤。
(1)收集数据,整理数据。
(2)根据资料和制表要求确定统计表的格式和项目。
(3)根据整理好的数据填表。
(4)填写总计与合计。
(5)注明统计表的名称、数量单位和制表日期。
2. 设计统计表。
逐项数出各个类别的数目,用画“正”字等方法整理。把收集的数据整理以后制成表格,用来反映情况,分析具体问题,这样的表格叫做统计表。统计表主要分为单式统计表和复式统计表。单式统计表只有一个统计项目,而复式统计表含有两个或两个以上统计项目。
例 四(1)班学生某次数学测验成绩记录如下。
用画“正”字的方法整理数据,再把统计表填写完整。
四(1)班学生某次数学测验成绩统计表
过程讲解 这是一道将四(1)班学生某次数学测验成绩进行整理,并制作统计表的题目。首先,可按照统计表中划分的分数段,对原始数据进行整理,在统计时要注意有序,做到不重复、不遗漏。“正”字中的每一笔画表示1人,1个“正”字表示5人。在制作统计表时,其中的“合计”表示将各个分数段的人数加起来,得出的合计人数应该和原始数据中的总人数相等。
解答: 100: 90~99: 80~89: 70~79: 60~69:
实战演练 1
五(1)班全体同学的左眼视力情况如下。
5.0 4.9 5.3 5.2 4.7 5.2
4.8 5.1 5.3 5.2 4.8 5.0
4.5 5.1 4.9 5.1 4.7 5.0
4.8 5.1 5.0 4.8 4.9 5.1
4.5 5.1 4.6 5.1 4.7 5.1
5.0 5.1 5.1 4.9 5.0 5.1
5.2 5.1 4.6 5.0 4.7 4.6
5.2 5.0 4.9 4.7 5.2 4.8
根据上面的数据,完成下面的统计表。
2
18
13
10
5
48
1. 条形统计图、折线统计图、扇形统计图的特点及作用。
2. 绘制统计图。
(1)绘制条形统计图的步骤和方法。
①画出两条互相垂直的射线;②在一条射线上适当分配条形的位置,确定直条的宽度和间隔;③在另一条射线上根据数据的大小,确定单位长度表示多少;④按照数据的多少画出长短不同的直条,并注明数量。
(2)绘制折线统计图的步骤和方法。
①画出两条互相垂直的射线;②在水平射线上适当分配折线的位置,确定折线的间隔;③在垂直射线上根据数据的大小,确定单位长度表示多少;④按照数据的大小先描出各点,再用线段顺次连接起来,并注明数量。
(3)绘制扇形统计图的步骤和方法。
①计算各部分数量占总量的百分之几;②计算表示各部分数量对应的扇形的圆心角度数;③画一个适当大小的圆,并按照上面所得的圆心角度数,在圆里画出各个扇形;④在每个扇形中标明所表示的各部分数量的名称及所占的百分数,并把各个扇形涂上不同的颜色或条纹加
以区分。
3. 分析统计图:会根据统计图进行数据分析,提出问题,并能作出简单的判断和预测。
例 (教材第 97 页)六(1)班同学的几项数据用统计表和统计图表示如下。
(1)根据以上统计图表,你得到了哪些信息?
(2)除了通过问卷调查收集数据外,还可以通过什么手段收集数据?
过程讲解 此题是对统计图、表特征掌握情况的考查。要根据各统计图、表的特征及所反映的相关数据来回答问题。不仅要发现一些表面的数据,而且还要从数据中发现更深层次的信息。
解答:(1)①从统计表中可以看出六(1)班有男生 22人,女生18人,全班总人数为40人。
②从扇形统计图中可以知道六(1)班男生人数占全班人数的55%,女生人数占全班人数的45%。
③条形统计图表示六(1)班男生和女生最喜欢的运动项目的人数,其中喜欢足球的男生人数比女生多,喜欢跳绳的女生人数比男生多,喜欢乒乓球的男生人数和女生同样多……
(2)还可以通过采访、收集各种媒体信息等方法收集数据。
实战演练 2
阅读下面的统计图,并回答问题。
某城市人均绿地面积变化情况统计图
(2012年~2016年)
(1)2013年该城市人均绿地面积比2012年增加了
多少平方米?增加了百分之几?(百分号前保留一
位小数)
0.4平方米
4.3%
(2)2015年该城市人均绿地面积比2016年少多少平方米?少百分之几?(百分号前保留一位小数)
0.4平方米
3.5%
1. 统计量的意义、作用和求法。
2. 可能性。
(1)生活中,有些事件的发生是不确定的,一般用“可能发生”来描述;有些事件的发生是确定的,一般用“一定发生”或“不可能发生”来描述。
(2)某些事情发生的可能性有大有小,当事件发生的可能性的大小与物体数量相关时,在总数或总体中物体数量越多,出现对应结果的可能性越大;物体数量越少,出现对应结果的可能性就越小。
3. 游戏规则的公平性。
根据事情发生的可能性大小设计游戏规则:当游戏双方机会均等时,游戏规则公平;当游戏双方机会不均等时,游戏规则不公平。
例 (教材第 97 页)六(1)班同学身高、体重情况如下表。
(1)上面两组数据的平均数各是多少?
(2)小组讨论,什么数据能代表全班同学的身高和体重?
(3)如果把全班同学编号,随意抽取一名学生,该生体重在36kg及以下的可能性大?还是在39kg及以上的可能性大?
过程讲解 平均数等于身高(体重)总和除以总人数;在这两组数据中,最大数据与最小数据相差不大,故用平均数可以反映这两组数据的一般水平;把全班同学编号,随意抽取一名学生,体重在36kg及以下的人数是11人,39kg及以上的人数是29人,29>11,所以体重在39kg及以上的可能性大。
解答:(1)第一组数据的平均数:(1.40×1+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3)÷(1+3+5+10+12+6+3)=60.17÷40≈1.50(m)
第二组数据的平均数:(30×2+33×4+36×5+39×12+42×10+45×4+48×3)÷(2+4+5+12+10+4+3)=1584÷40=39.6(kg)
(2)平均数能代表全班同学的身高和体重。
(3)把全班同学编号,随意抽取一名学生,该生体重在39kg 及以上的可能性大。
实战演练 3
下面是某商场2017年7月电冰箱的销售情况统计表。
(1)这组数据的平均数、中位数和众数各是多少?
(除不尽的保留一位小数)
10.5 10 10
(2)你认为用哪一个数据来表示销售员的销售水平比较合适呢?
用中位数10或众数10表示比较合适。
(3)如果把销售员编号,随意抽取一位,该销售员
销售台数在10台的可能性大还是12台的可能性大?
10 台的可能性大。
