人教版数学六年级下册期末复习课件-6.4 数学思考 课件(33张PPT)
文档属性
| 名称 | 人教版数学六年级下册期末复习课件-6.4 数学思考 课件(33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 618.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 18:36:02 | ||
图片预览











文档简介
(共33张PPT)
6.4 数学思考
根据给定的图形或数字,探索其中简单的排列规律,解决生活中的实际问题。
例 (教材第 100 页)6个点可以连多少条线段?8个点呢?根据规律,你知道12个点、20个点能连多少条线段吗?请写出算式。想一想,n个点能连多少条线段?
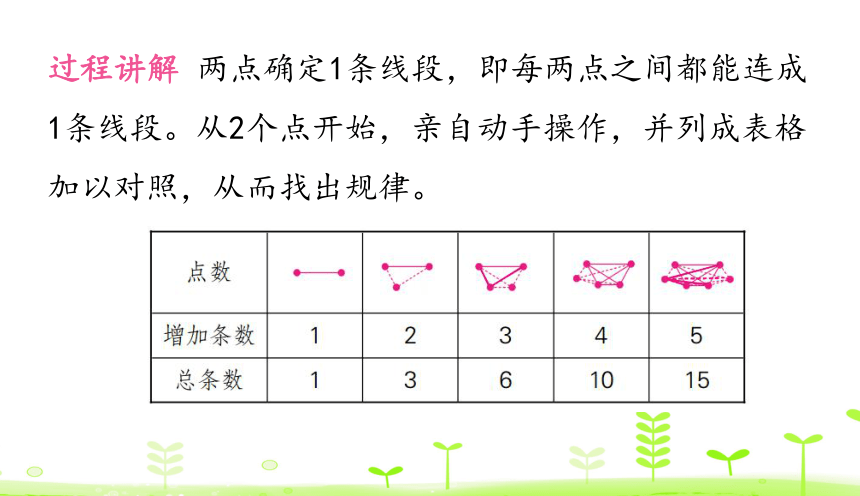
过程讲解 两点确定1条线段,即每两点之间都能连成1条线段。从2个点开始,亲自动手操作,并列成表格加以对照,从而找出规律。
通过观察发现:2个点可以连成1条线段,从2个点开始,以后每增加1个点,这个点和原有的每个点都能连成1条线段,所以原来有几个点,就会相应地增加几条线段。
即2个点共连线段:1条
3个点共连线段:1+2=3(条)
4个点共连线段:1+2+3=6(条)
5个点共连线段:1+2+3+4=10(条)
6个点共连线段:1+2+3+4+5=15(条)
8个点共连线段:1+2+3+4+5+6+7=28(条)
推出:n个点共连线段:1+2+3+4+…+(n-1)=
根据规律可以计算出 12 个点、20 个点能连多少条线段。
解答:6 个点共连线段:1+2+3+4+5=15(条)
8 个点共连线段:1+2+3+4+5+6+7=28(条)
12 个点共连线段: ×12×(12-1)=66(条)
20 个点共连线段: ×20×(20-1)=190(条)
n 个点共连线段:1+2+3+4+…+(n-1)=
实战演练 1
填空题。
(1)在 这列分数中,第10 个分数是( )。
(2)王翔按照一定的规律写数 :1,+2,-3,4,+5,-6,7,+8,-9,…一共写了 50 个数。他写的数中一共有( )个正数,( )个负数。
10
29
34
16
(3)某体育馆用大小相同的长方形地板铺地面,
第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3……按照此方法,第5次铺完后,所使用的地板一共有( )块。第n次铺完后,用含有字母n的式子表示所使用的地板是( )块。
90
2n(2n-1)
解答推理问题一般可以从以下几方面考虑:
(1)选准突破口,分析时综合几个条件进行判断。
(2)根据题中条件,在推理过程中,不断排除不可能的情况,从而得出要求的结论。
(3)对可能出现的情况做出假设,然后再根据条件推理,如果得到的结论和条件不矛盾,说明假设是正确的。
(4)遇到比较复杂的推理问题,可以借助图表进行分析。
例 (教材第101页)六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有 B、D、E;第三次有 A、E、F。请问:哪两位班长是同班的?
过程讲解 这是一道比较复杂的逻辑推理问题,每次开班长会时,每班一位班长参加,已知 3次到会的班长,判断哪两位班长是同班的,可借助列表进行对比、排除,从而推导出结论。用数字“1”表示到会,用数字“0”表示没到会。可以用下面的表格呈现题意:
从第一次到会的情况可以看出:A与B、C不是同班,A 只可能和D、E、F同班。从第二次到会的情况可以看出:A没有参加,由第一次的到会情况知B和A不是同班,A只可能和D、E 同班。从第三次到会的情况可以看出:A 与 E、F不是同班,结合第一次与第二次的到会情况,A只可能和D同班。
确定了A和D同班后,B、C、E、F的关系如下:
从第一次到会的情况可以看出:B、C不是同班,B只可能和E、F同班。
从第二次到会的情况可以看出:B、E不是同班,结合第一次的到会情况知,B只可能和F同班。
由以上可知C和E同班。
解答::A和D两位班长同班,B和F两位班长同班,C和E两位班长同班。
实战演练 2
1. 学校组织了足球、航模和电脑兴趣小组,淘气、笑笑和小明分别参加了其中一项。笑笑不喜欢踢足球,小明不是电脑兴趣小组的,淘气喜欢航模。你知道他们分别参加的是什么兴趣小组吗?
淘气:航模 笑笑:电脑 小明:足球
2. 张老师、王老师和李老师三位老师,其中一位教美术、一位教音乐、一位教书法。已知:
(1)张老师比教音乐的老师年龄大;
(2)王老师比教美术的老师年龄小;
(3)教美术的老师比李老师年龄小。
请问三位老师各教什么课?
张老师:教美术 王老师:教音乐 李老师:教书法
质量相等的物体可以相互代换,渗透的就是等量代换的数学思想。它是方程解法的重要原理,解题时可将某个条件用其他相等的条件进行代换。等量代换用等式的性质来体现就是等式的传递性:如果a=b,b=c,那么a=c。
实战演练 3
1. △+□=250 □=△+△+△+△
△=? □=?
△=50 □=200
2. △+□=60 □+○=51
△+○=39
△=? □=? ○=?
△=24 □=36 ○=15
3. ○+□+□=24 ○+□=△
△=○+○+3
○=? □=? △=?
○=6 □=9 △=15
1. 认识平角。
一条射线绕它的端点旋转,当始边和终边在同一条直线上,且方向相反时,构成的角叫做平角。平角是一种比较特殊的角,平角=180毅。
2. 平角与直线的区别。
直线没有端点;平角有两条边和一个顶点。平角的两条边在一条直线上,是从角的顶点出发的两条射线。
实战演练 4
如下图,把三角形ABC的边AB向两边延长,边AB延长到点D,再反向延长至点E。
(1)图中共有几个平角?
2 个
(2)你能说明∠5=∠2+∠3吗?
因为∠1+∠2+∠3=180°,∠1+∠5=180°,
等式两边都减去∠1,可以得到∠2+∠3=180°-∠1,∠5=180°-∠1,所以∠5=∠2+∠3。
要求组合数,常用的方法是枚举法(列举或图示出所有可能),在枚举时为避免重复或遗漏,要注意有顺序地思考。
1. 加法原理。
做一件事情,完成它有n类办法,在第一类办法中有m1种不同的方法,在第二类方法中有m2种不同的方法,…,在第n类办法中有mn种不同的方法,那么完成这件事情共有m1+m2+m3+…+mn种不同的方法。
2. 乘法原理。
做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有 m1·m2·m3·…·mn 种不同的方法。
例 如图,从A市到B市有2条不同的路,从B市到C市
有5条不同的路。若从A市经过B市到C市,则有多少条不同的路可以走?
过程讲解 从A市到B市有2条路,从B市到C市有5条路,由A市到B市的每一条路都可以和B市到C市的5条路组合,因此就有2个5种不同的走法。
解答:2×5=10(条)
答:从A市经过B市到C市,有10条不同的路可以走。
实战演练 5
某商店有两种电话机,一种是按键的,一种是转盘的。每种电话机又有红、黄、绿3种颜色,一共有多少种款式的电话机可供顾客选择?
2×3=6(种)
答:一共有6种款式的电话机可供顾客选择。
6.4 数学思考
根据给定的图形或数字,探索其中简单的排列规律,解决生活中的实际问题。
例 (教材第 100 页)6个点可以连多少条线段?8个点呢?根据规律,你知道12个点、20个点能连多少条线段吗?请写出算式。想一想,n个点能连多少条线段?
过程讲解 两点确定1条线段,即每两点之间都能连成1条线段。从2个点开始,亲自动手操作,并列成表格加以对照,从而找出规律。
通过观察发现:2个点可以连成1条线段,从2个点开始,以后每增加1个点,这个点和原有的每个点都能连成1条线段,所以原来有几个点,就会相应地增加几条线段。
即2个点共连线段:1条
3个点共连线段:1+2=3(条)
4个点共连线段:1+2+3=6(条)
5个点共连线段:1+2+3+4=10(条)
6个点共连线段:1+2+3+4+5=15(条)
8个点共连线段:1+2+3+4+5+6+7=28(条)
推出:n个点共连线段:1+2+3+4+…+(n-1)=
根据规律可以计算出 12 个点、20 个点能连多少条线段。
解答:6 个点共连线段:1+2+3+4+5=15(条)
8 个点共连线段:1+2+3+4+5+6+7=28(条)
12 个点共连线段: ×12×(12-1)=66(条)
20 个点共连线段: ×20×(20-1)=190(条)
n 个点共连线段:1+2+3+4+…+(n-1)=
实战演练 1
填空题。
(1)在 这列分数中,第10 个分数是( )。
(2)王翔按照一定的规律写数 :1,+2,-3,4,+5,-6,7,+8,-9,…一共写了 50 个数。他写的数中一共有( )个正数,( )个负数。
10
29
34
16
(3)某体育馆用大小相同的长方形地板铺地面,
第1次铺2块,如图1;第2次把第1次铺的完全围起来,如图2;第3次把第2次铺的完全围起来,如图3……按照此方法,第5次铺完后,所使用的地板一共有( )块。第n次铺完后,用含有字母n的式子表示所使用的地板是( )块。
90
2n(2n-1)
解答推理问题一般可以从以下几方面考虑:
(1)选准突破口,分析时综合几个条件进行判断。
(2)根据题中条件,在推理过程中,不断排除不可能的情况,从而得出要求的结论。
(3)对可能出现的情况做出假设,然后再根据条件推理,如果得到的结论和条件不矛盾,说明假设是正确的。
(4)遇到比较复杂的推理问题,可以借助图表进行分析。
例 (教材第101页)六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有 B、D、E;第三次有 A、E、F。请问:哪两位班长是同班的?
过程讲解 这是一道比较复杂的逻辑推理问题,每次开班长会时,每班一位班长参加,已知 3次到会的班长,判断哪两位班长是同班的,可借助列表进行对比、排除,从而推导出结论。用数字“1”表示到会,用数字“0”表示没到会。可以用下面的表格呈现题意:
从第一次到会的情况可以看出:A与B、C不是同班,A 只可能和D、E、F同班。从第二次到会的情况可以看出:A没有参加,由第一次的到会情况知B和A不是同班,A只可能和D、E 同班。从第三次到会的情况可以看出:A 与 E、F不是同班,结合第一次与第二次的到会情况,A只可能和D同班。
确定了A和D同班后,B、C、E、F的关系如下:
从第一次到会的情况可以看出:B、C不是同班,B只可能和E、F同班。
从第二次到会的情况可以看出:B、E不是同班,结合第一次的到会情况知,B只可能和F同班。
由以上可知C和E同班。
解答::A和D两位班长同班,B和F两位班长同班,C和E两位班长同班。
实战演练 2
1. 学校组织了足球、航模和电脑兴趣小组,淘气、笑笑和小明分别参加了其中一项。笑笑不喜欢踢足球,小明不是电脑兴趣小组的,淘气喜欢航模。你知道他们分别参加的是什么兴趣小组吗?
淘气:航模 笑笑:电脑 小明:足球
2. 张老师、王老师和李老师三位老师,其中一位教美术、一位教音乐、一位教书法。已知:
(1)张老师比教音乐的老师年龄大;
(2)王老师比教美术的老师年龄小;
(3)教美术的老师比李老师年龄小。
请问三位老师各教什么课?
张老师:教美术 王老师:教音乐 李老师:教书法
质量相等的物体可以相互代换,渗透的就是等量代换的数学思想。它是方程解法的重要原理,解题时可将某个条件用其他相等的条件进行代换。等量代换用等式的性质来体现就是等式的传递性:如果a=b,b=c,那么a=c。
实战演练 3
1. △+□=250 □=△+△+△+△
△=? □=?
△=50 □=200
2. △+□=60 □+○=51
△+○=39
△=? □=? ○=?
△=24 □=36 ○=15
3. ○+□+□=24 ○+□=△
△=○+○+3
○=? □=? △=?
○=6 □=9 △=15
1. 认识平角。
一条射线绕它的端点旋转,当始边和终边在同一条直线上,且方向相反时,构成的角叫做平角。平角是一种比较特殊的角,平角=180毅。
2. 平角与直线的区别。
直线没有端点;平角有两条边和一个顶点。平角的两条边在一条直线上,是从角的顶点出发的两条射线。
实战演练 4
如下图,把三角形ABC的边AB向两边延长,边AB延长到点D,再反向延长至点E。
(1)图中共有几个平角?
2 个
(2)你能说明∠5=∠2+∠3吗?
因为∠1+∠2+∠3=180°,∠1+∠5=180°,
等式两边都减去∠1,可以得到∠2+∠3=180°-∠1,∠5=180°-∠1,所以∠5=∠2+∠3。
要求组合数,常用的方法是枚举法(列举或图示出所有可能),在枚举时为避免重复或遗漏,要注意有顺序地思考。
1. 加法原理。
做一件事情,完成它有n类办法,在第一类办法中有m1种不同的方法,在第二类方法中有m2种不同的方法,…,在第n类办法中有mn种不同的方法,那么完成这件事情共有m1+m2+m3+…+mn种不同的方法。
2. 乘法原理。
做一件事,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有 m1·m2·m3·…·mn 种不同的方法。
例 如图,从A市到B市有2条不同的路,从B市到C市
有5条不同的路。若从A市经过B市到C市,则有多少条不同的路可以走?
过程讲解 从A市到B市有2条路,从B市到C市有5条路,由A市到B市的每一条路都可以和B市到C市的5条路组合,因此就有2个5种不同的走法。
解答:2×5=10(条)
答:从A市经过B市到C市,有10条不同的路可以走。
实战演练 5
某商店有两种电话机,一种是按键的,一种是转盘的。每种电话机又有红、黄、绿3种颜色,一共有多少种款式的电话机可供顾客选择?
2×3=6(种)
答:一共有6种款式的电话机可供顾客选择。
