人教版数学六年级下册期末复习课件6.2.2 图形的认识与测量(二)立体图形 课件(23张PPT)
文档属性
| 名称 | 人教版数学六年级下册期末复习课件6.2.2 图形的认识与测量(二)立体图形 课件(23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 788.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-14 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
6.2.2 图形的认识与测量(二)立体图形
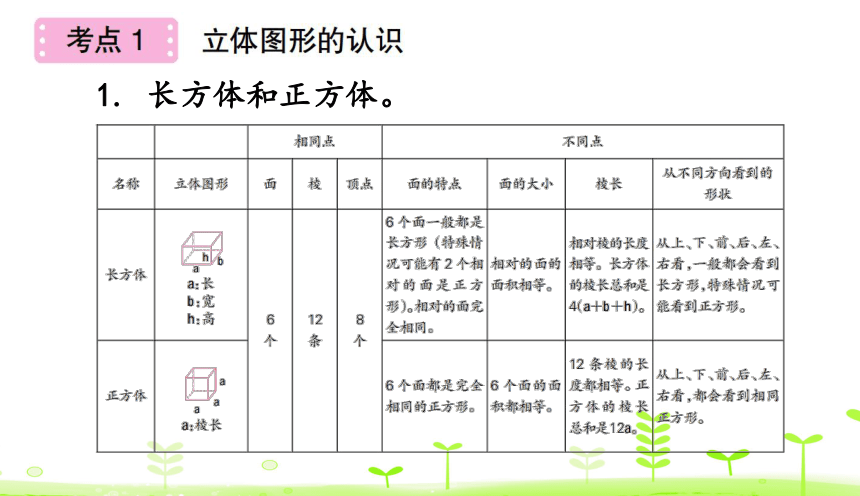
1. 长方体和正方体。
2. 圆柱和圆锥。
例1 一个正方体的棱长是5厘米,那么这个正方体的棱长总和是多少厘米?
过程讲解 此题考查的是正方体棱长总和的计算公式。正方体有12条棱,并且每条棱长都相等。已知棱长是 5厘米,所以棱长总和是5×12=60(厘米)。
解答:5×12=60(厘米)
答:这个正方体的棱长总和是 60 厘米。
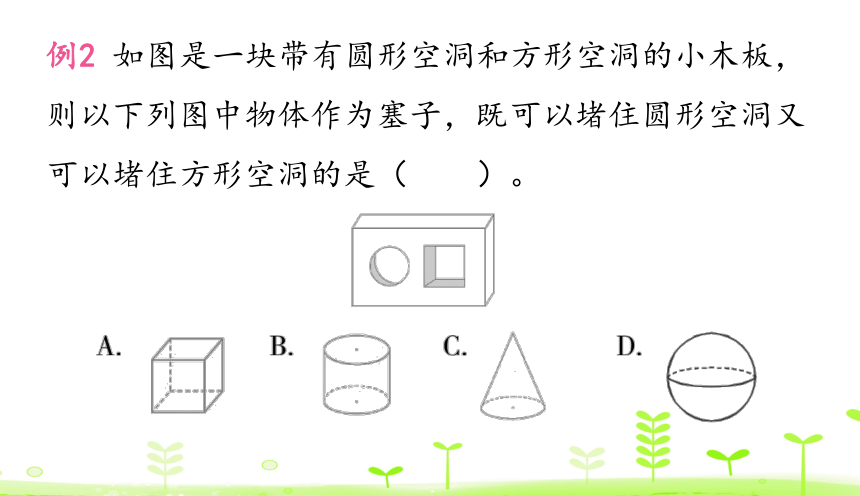
例2 如图是一块带有圆形空洞和方形空洞的小木板,则以下列图中物体作为塞子,既可以堵住圆形空洞又可以堵住方形空洞的是( )。
过程讲解 从上面看圆柱是个圆,可以堵住圆形空洞,从侧面看它是长方形,可以堵住方形空洞,据此选择B。
解答:B
实战演练 1
1. 判断题。(对的打“√”,错的打“×”)
(1)以正方形或长方形的一边为轴旋转一周会形成一个圆柱。 ( )
(2)圆锥有无数条高。 ( )
√
×
(3)长方体中最多有2个面是正方形。 ( )
(4)从圆锥的侧面看,会看到一个圆。 ( )
√
×
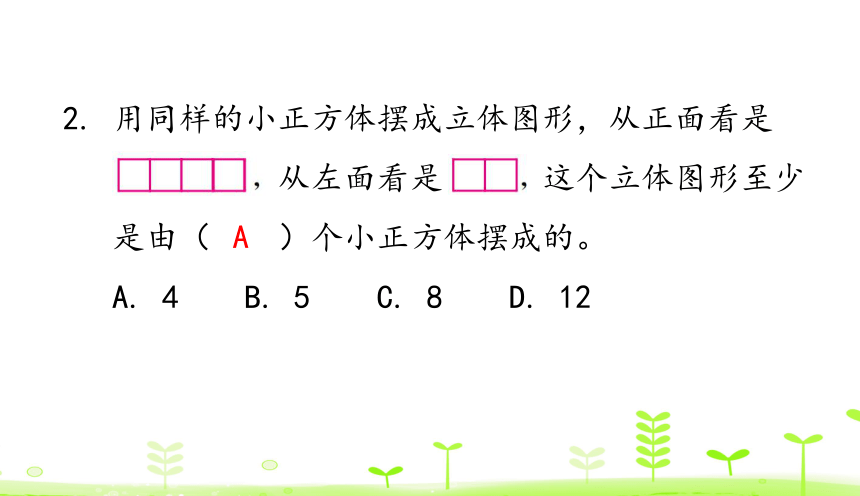
2. 用同样的小正方体摆成立体图形,从正面看是
从左面看是 这个立体图形至少
是由( )个小正方体摆成的。
A. 4 B. 5 C. 8 D. 12
A
例1 某体育馆要建一个长方体游泳池,该游泳池的长是60米,宽是40米,深是2米。如果要在池的四周和底面都贴上瓷砖,共需要贴多少平方米的瓷砖?
过程讲解 因为游泳池是长方体形状,但贴瓷砖的面有 5个,我们只需求出这5个面的面积和。还可以先利用长方体表面积的计算公式,算出6个面的总和,再减去一个上面的面积。
解答:60×40+(60+40)×2×2=2800(平方米)
或(60×40+60×2+40×2)×2-60×40=2800(平方米)
答:共需要贴 2800 平方米的瓷砖。
例2 把一个底面直径是8厘米、高是9厘米的圆锥形铅锤浸没在一个底面积是200.96平方厘米的圆柱形容器中(水未溢出),当把铅锤从水中取出后,圆柱形容器中的水面下降了几厘米?
过程讲解 此题是对圆柱和圆锥体积公式的考查。解此题的关键就要理解圆柱形容器里下降的水的体积就是圆锥形铅锤的体积。根据公式V= 先求出铅锤的体积,然后用体积除以圆柱形容器的底面积,求出水面下降的高度。
解答: ×3.14×(8÷2) ×9÷200.96=0.75(厘米)
答:圆柱形容器中的水面下降了0.75厘米。
例3 把一根长2m的圆柱形钢材截成四段,它的表面积就增加了9.42cm 。原来这根圆柱形钢材的体积是多少?
过程讲解 将这根圆柱形钢材截成四段,实际上就增加了6个横截面的面积。根据圆柱的体积等于底面积乘高,可以求出这根圆柱形钢材的体积。
解答:2m=200cm 9.42÷6×200=314(cm )
答:原来这根圆柱形钢材的体积是 314cm 。
实战演练 2
1. 填空题。
(1)下图是一个立体图形的展开图。(单位:cm)
①这个展开图可以折成一个( )体。
②折成的立体图形中长度是4cm的棱有( )条,长度是8cm的棱有( )条。
③这个立体图形的表面积是( )cm ,体积是( )cm 。
长方
8
4
160
128
一个圆锥与一个圆柱的体积和底面积都相等,圆锥的高是圆柱的高的( )倍。
3
2. 一辆货车车厢是长方体,它的长是4米,宽是1.5米,高是4米(从里面量)。装满一车沙,卸车后沙堆成一个高5分米的圆锥形,它的底面积是多少?
5分米=0.5米
4×1.5×4×3÷0.5=144(平方米)
答:它的底面积是144平方米。
6.2.2 图形的认识与测量(二)立体图形
1. 长方体和正方体。
2. 圆柱和圆锥。
例1 一个正方体的棱长是5厘米,那么这个正方体的棱长总和是多少厘米?
过程讲解 此题考查的是正方体棱长总和的计算公式。正方体有12条棱,并且每条棱长都相等。已知棱长是 5厘米,所以棱长总和是5×12=60(厘米)。
解答:5×12=60(厘米)
答:这个正方体的棱长总和是 60 厘米。
例2 如图是一块带有圆形空洞和方形空洞的小木板,则以下列图中物体作为塞子,既可以堵住圆形空洞又可以堵住方形空洞的是( )。
过程讲解 从上面看圆柱是个圆,可以堵住圆形空洞,从侧面看它是长方形,可以堵住方形空洞,据此选择B。
解答:B
实战演练 1
1. 判断题。(对的打“√”,错的打“×”)
(1)以正方形或长方形的一边为轴旋转一周会形成一个圆柱。 ( )
(2)圆锥有无数条高。 ( )
√
×
(3)长方体中最多有2个面是正方形。 ( )
(4)从圆锥的侧面看,会看到一个圆。 ( )
√
×
2. 用同样的小正方体摆成立体图形,从正面看是
从左面看是 这个立体图形至少
是由( )个小正方体摆成的。
A. 4 B. 5 C. 8 D. 12
A
例1 某体育馆要建一个长方体游泳池,该游泳池的长是60米,宽是40米,深是2米。如果要在池的四周和底面都贴上瓷砖,共需要贴多少平方米的瓷砖?
过程讲解 因为游泳池是长方体形状,但贴瓷砖的面有 5个,我们只需求出这5个面的面积和。还可以先利用长方体表面积的计算公式,算出6个面的总和,再减去一个上面的面积。
解答:60×40+(60+40)×2×2=2800(平方米)
或(60×40+60×2+40×2)×2-60×40=2800(平方米)
答:共需要贴 2800 平方米的瓷砖。
例2 把一个底面直径是8厘米、高是9厘米的圆锥形铅锤浸没在一个底面积是200.96平方厘米的圆柱形容器中(水未溢出),当把铅锤从水中取出后,圆柱形容器中的水面下降了几厘米?
过程讲解 此题是对圆柱和圆锥体积公式的考查。解此题的关键就要理解圆柱形容器里下降的水的体积就是圆锥形铅锤的体积。根据公式V= 先求出铅锤的体积,然后用体积除以圆柱形容器的底面积,求出水面下降的高度。
解答: ×3.14×(8÷2) ×9÷200.96=0.75(厘米)
答:圆柱形容器中的水面下降了0.75厘米。
例3 把一根长2m的圆柱形钢材截成四段,它的表面积就增加了9.42cm 。原来这根圆柱形钢材的体积是多少?
过程讲解 将这根圆柱形钢材截成四段,实际上就增加了6个横截面的面积。根据圆柱的体积等于底面积乘高,可以求出这根圆柱形钢材的体积。
解答:2m=200cm 9.42÷6×200=314(cm )
答:原来这根圆柱形钢材的体积是 314cm 。
实战演练 2
1. 填空题。
(1)下图是一个立体图形的展开图。(单位:cm)
①这个展开图可以折成一个( )体。
②折成的立体图形中长度是4cm的棱有( )条,长度是8cm的棱有( )条。
③这个立体图形的表面积是( )cm ,体积是( )cm 。
长方
8
4
160
128
一个圆锥与一个圆柱的体积和底面积都相等,圆锥的高是圆柱的高的( )倍。
3
2. 一辆货车车厢是长方体,它的长是4米,宽是1.5米,高是4米(从里面量)。装满一车沙,卸车后沙堆成一个高5分米的圆锥形,它的底面积是多少?
5分米=0.5米
4×1.5×4×3÷0.5=144(平方米)
答:它的底面积是144平方米。
