高中数学人教B版必修三:7.3.1 正弦函数的性质与图像 课件(63张ppt)
文档属性
| 名称 | 高中数学人教B版必修三:7.3.1 正弦函数的性质与图像 课件(63张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 11.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-16 00:00:00 | ||
图片预览









文档简介
(共63张PPT)
正弦函数的性质与图像
高一年级 数学
研究函数的一般方法
图像
数形结合
性质
(定义域、奇偶性、周期性、单调性、值域、零点等)
性质
情境与问题
到地面的高 m
转轮半径 m
以 为终边的角为 rad
点 离地面的高度为 m
情境与问题
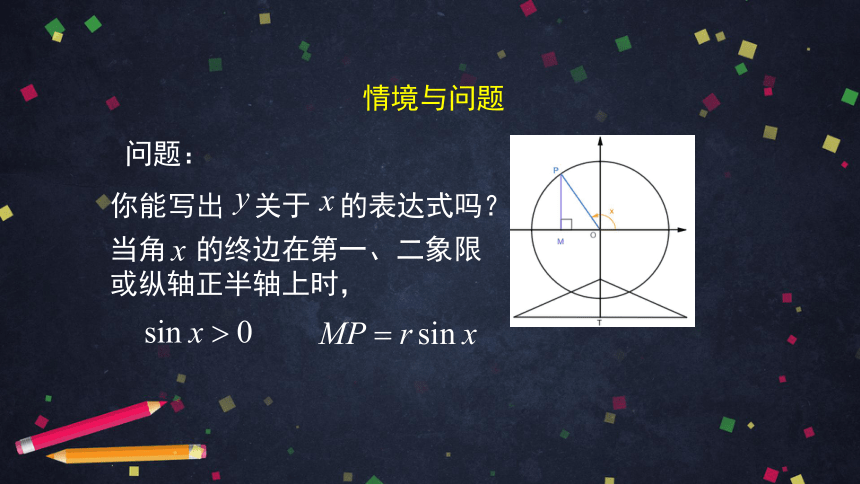
问题:
你能写出 关于 的表达式吗?
当角 的终边在第一、二象限
或纵轴正半轴上时,
情境与问题
问题:
你能写出 关于 的表达式吗?
当角 的终边在第三、四象限
或纵轴负半轴上时,
情境与问题
问题:
你能写出 关于 的表达式吗?
当角 的终边在横轴上时,
情境与问题
对于任意一个角 ,都有唯一确定的正弦 与之对应,因此 是一个函数,一般称为正弦函数.
问题:
是 的函数吗?这个函数有什么性质呢?
正弦函数的性质
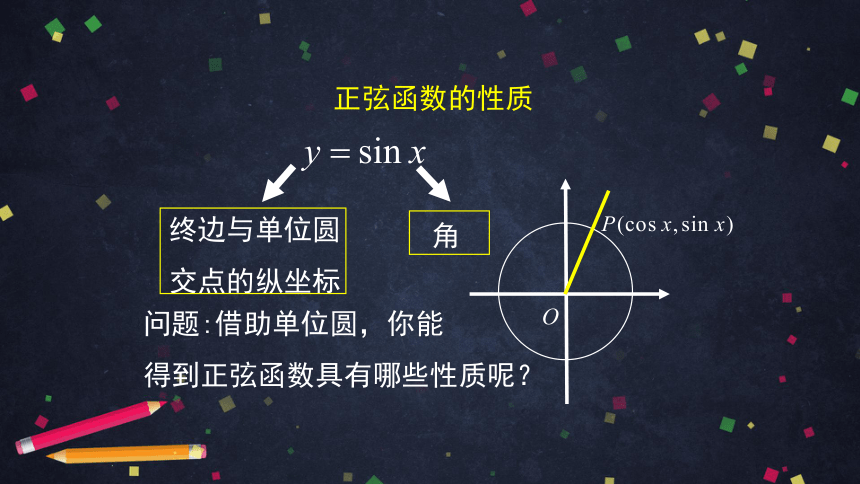
问题:借助单位圆,你能
得到正弦函数具有哪些性质呢?
终边与单位圆
交点的纵坐标
角
正弦函数的性质
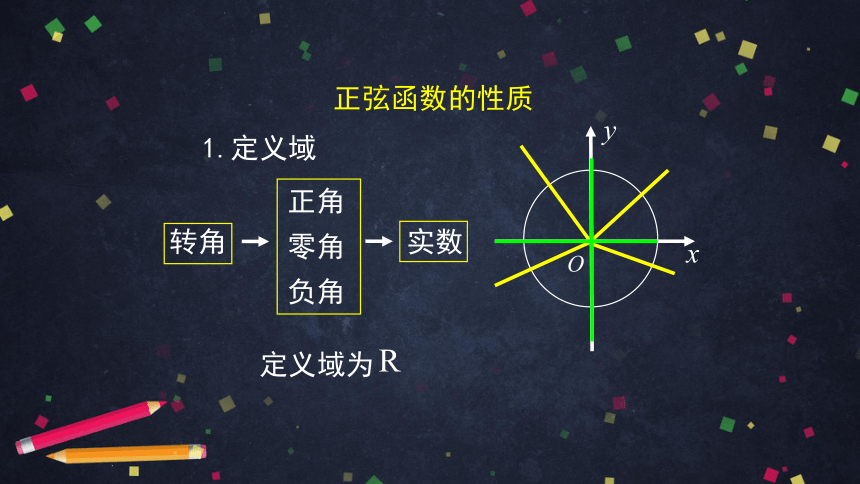
1.定义域
正角
零角
负角
转角
实数
定义域为
正弦函数的性质
1.定义域
对任意的角 来说,设 是 终边上异于原点的任意一点, ,
定义域为
正弦
角的终边位置
正弦函数的性质
2.奇偶性
一般地,函数 的定义域为 ,
,都有 ,
奇函数
偶函数
正弦函数的性质
2.奇偶性
问题:角 和 的终边与单位圆
交点纵坐标的关系?
与 的终边的关系?
关于 轴对称 纵坐标互为相反数
正弦函数的性质
2.奇偶性
交点纵坐标
相反数
交点纵坐标
正弦函数的性质
2.奇偶性
交点纵坐标
相反数
交点纵坐标
诱导公式
正弦函数是奇函数,图像关于原点中心对称
正弦函数的性质
3.对称性
问题:正弦函数还有其它
的对称中心吗?
正弦函数的图像
问题:你能用所学知识严格证明正弦曲线
关于 中心对称吗?
正弦函数的图像
问题:你能用所学知识严格证明正弦曲线
关于 中心对称吗?
正弦函数的性质
3.对称性
问题:正弦函数还有其它
的对称性吗?
正弦函数关于直线 对称
正弦函数的性质
3.对称性
正弦函数关于直线 对称
正弦函数的性质
问题:从交点纵坐标的变化,你能观察出正弦函数是否具有周期性呢?
4.周期性
正弦函数的性质
终边旋转整数圈
4.周期性
交点纵坐标重复出现
终边相同的角
正弦值
正弦函数的性质
4.周期性
问题:正弦函数的周期
是多少呢?
是周期吗?
正弦函数的性质
4.周期性
问题:正弦函数的周期
是多少呢?
正弦函数的性质
4.周期性
问题:正弦函数的周期
是多少呢?
不是周期
正弦函数的性质
4.周期性
周期:
最小正周期:
正弦函数的性质
4.周期性
问题:你能抽象出一般函数周期性的定义吗?
1.定义域中的每一个自变量
2.自变量增加或减少同一个非零常数时,函数值总是相等的。
正弦函数的性质
4.周期性
问题:你能抽象出一般函数周期性的定义吗?
1.定义域中的每一个自变量
2.自变量增加或减少同一个非零常数时,函数值总是相等的。
正弦函数的性质
一般地,对于函数 ,如果存在一个非零常数 ,使得对定义域内的每一个 ,都满足
那么就称函数 为周期函数,非零常数 称
为这个函数的周期.
正弦函数的性质
函数的性质
单调性
奇偶性
周期性
正弦函数的性质
问题:从交点纵坐标的变化,你能得到正弦函数的单调性吗?
5.单调性
周期性
正弦函数的性质
5.单调性
正弦函数的性质
5.单调性
正弦函数的性质
单调递增区间
单调递减区间
5.单调性
正弦函数的性质
6.值域(最值)
值域为
正弦函数的性质
角的终边落在 轴上
6.零点
正弦函数的性质
单位圆
角终边与单位圆交点的纵坐标
直观化解释模型
正弦函数
数形结合
正弦函数的图像
问题:正弦函数的性质对作出正弦函数的图像有什么帮助呢?
列表描点
周期性 长度为 的闭区间
奇偶性 关于原点对称
对称性 关于 对称
正弦函数的图像
问题:
正弦函数 在闭区间 递增,
图像的大致形状是怎样的呢?是一条直线?
是增加的越来越快?还是越来越慢呢?
正弦函数的图像
角的变化量
函数值变化量
交点纵坐标
的变化量
正弦函数的图像
列表
正弦函数的图像
描点
连线
正弦函数的图像
正弦函数的图像
正弦函数的图像
正弦函数的图像
正弦函数的图像
正弦函数在对称轴和对称中心处的函数值
有什么特征呢?
正弦函数的图像
问题:观察正弦函数的图像,你能说出在确定
的图像形状时,哪些点起着关键作用?为什么?
开口,对称轴
顶点,交点
单调性、渐近线、与轴的交点
性质 图像 形状特征 示意图
正弦函数的图像
五点作图法
波峰波谷的平缓过渡
对称中心左右曲线凹凸
正弦函数的性质与图像
数缺形时少直观,形缺数时难入微
五点作图
数形结合
借助单位圆分析性质
借助性质利用单位圆研究图像
根据图像进一步理解性质
例:不求值,比较 和 的大小.
单位圆
正弦函数的单调性
分析:求函数最值的本质是什么呢?
值域 函数的单调性
这类函数的最值问题如何处理呢?
换元法
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:函数 与 同时取得最值,
所以
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:令 ,则
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:根据二次函数闭区间上的单调性,可得
即 此时
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:根据二次函数闭区间上的单调性,
可得 即
或 ,此时
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
例:用五点法作函数 的图像.
解:找关键的五个点,列表如下
例:用五点法作函数 的图像.
解:描点作图
位置关系?
向上平移
1个单位
小结
正弦函数
单位圆
抽象
函数图像
直观
数
形
核心任务:利用单位圆研究正弦函数的性质与图像
同角三角函数基本关系式
诱导公式
变量间的变化过程
变化趋势
作业
1.不求值,比较 和 的大小.
作业
2.求下列函数的最大值和最小值,并求出取得最大值和
最小值时 的值.
(1) (2) (3)
作业
3.用五点法作出下列函数在 上的图像,并说明它
们与 的图像的关系.
(1) (2)
感谢观看
正弦函数的性质与图像
高一年级 数学
研究函数的一般方法
图像
数形结合
性质
(定义域、奇偶性、周期性、单调性、值域、零点等)
性质
情境与问题
到地面的高 m
转轮半径 m
以 为终边的角为 rad
点 离地面的高度为 m
情境与问题
问题:
你能写出 关于 的表达式吗?
当角 的终边在第一、二象限
或纵轴正半轴上时,
情境与问题
问题:
你能写出 关于 的表达式吗?
当角 的终边在第三、四象限
或纵轴负半轴上时,
情境与问题
问题:
你能写出 关于 的表达式吗?
当角 的终边在横轴上时,
情境与问题
对于任意一个角 ,都有唯一确定的正弦 与之对应,因此 是一个函数,一般称为正弦函数.
问题:
是 的函数吗?这个函数有什么性质呢?
正弦函数的性质
问题:借助单位圆,你能
得到正弦函数具有哪些性质呢?
终边与单位圆
交点的纵坐标
角
正弦函数的性质
1.定义域
正角
零角
负角
转角
实数
定义域为
正弦函数的性质
1.定义域
对任意的角 来说,设 是 终边上异于原点的任意一点, ,
定义域为
正弦
角的终边位置
正弦函数的性质
2.奇偶性
一般地,函数 的定义域为 ,
,都有 ,
奇函数
偶函数
正弦函数的性质
2.奇偶性
问题:角 和 的终边与单位圆
交点纵坐标的关系?
与 的终边的关系?
关于 轴对称 纵坐标互为相反数
正弦函数的性质
2.奇偶性
交点纵坐标
相反数
交点纵坐标
正弦函数的性质
2.奇偶性
交点纵坐标
相反数
交点纵坐标
诱导公式
正弦函数是奇函数,图像关于原点中心对称
正弦函数的性质
3.对称性
问题:正弦函数还有其它
的对称中心吗?
正弦函数的图像
问题:你能用所学知识严格证明正弦曲线
关于 中心对称吗?
正弦函数的图像
问题:你能用所学知识严格证明正弦曲线
关于 中心对称吗?
正弦函数的性质
3.对称性
问题:正弦函数还有其它
的对称性吗?
正弦函数关于直线 对称
正弦函数的性质
3.对称性
正弦函数关于直线 对称
正弦函数的性质
问题:从交点纵坐标的变化,你能观察出正弦函数是否具有周期性呢?
4.周期性
正弦函数的性质
终边旋转整数圈
4.周期性
交点纵坐标重复出现
终边相同的角
正弦值
正弦函数的性质
4.周期性
问题:正弦函数的周期
是多少呢?
是周期吗?
正弦函数的性质
4.周期性
问题:正弦函数的周期
是多少呢?
正弦函数的性质
4.周期性
问题:正弦函数的周期
是多少呢?
不是周期
正弦函数的性质
4.周期性
周期:
最小正周期:
正弦函数的性质
4.周期性
问题:你能抽象出一般函数周期性的定义吗?
1.定义域中的每一个自变量
2.自变量增加或减少同一个非零常数时,函数值总是相等的。
正弦函数的性质
4.周期性
问题:你能抽象出一般函数周期性的定义吗?
1.定义域中的每一个自变量
2.自变量增加或减少同一个非零常数时,函数值总是相等的。
正弦函数的性质
一般地,对于函数 ,如果存在一个非零常数 ,使得对定义域内的每一个 ,都满足
那么就称函数 为周期函数,非零常数 称
为这个函数的周期.
正弦函数的性质
函数的性质
单调性
奇偶性
周期性
正弦函数的性质
问题:从交点纵坐标的变化,你能得到正弦函数的单调性吗?
5.单调性
周期性
正弦函数的性质
5.单调性
正弦函数的性质
5.单调性
正弦函数的性质
单调递增区间
单调递减区间
5.单调性
正弦函数的性质
6.值域(最值)
值域为
正弦函数的性质
角的终边落在 轴上
6.零点
正弦函数的性质
单位圆
角终边与单位圆交点的纵坐标
直观化解释模型
正弦函数
数形结合
正弦函数的图像
问题:正弦函数的性质对作出正弦函数的图像有什么帮助呢?
列表描点
周期性 长度为 的闭区间
奇偶性 关于原点对称
对称性 关于 对称
正弦函数的图像
问题:
正弦函数 在闭区间 递增,
图像的大致形状是怎样的呢?是一条直线?
是增加的越来越快?还是越来越慢呢?
正弦函数的图像
角的变化量
函数值变化量
交点纵坐标
的变化量
正弦函数的图像
列表
正弦函数的图像
描点
连线
正弦函数的图像
正弦函数的图像
正弦函数的图像
正弦函数的图像
正弦函数的图像
正弦函数在对称轴和对称中心处的函数值
有什么特征呢?
正弦函数的图像
问题:观察正弦函数的图像,你能说出在确定
的图像形状时,哪些点起着关键作用?为什么?
开口,对称轴
顶点,交点
单调性、渐近线、与轴的交点
性质 图像 形状特征 示意图
正弦函数的图像
五点作图法
波峰波谷的平缓过渡
对称中心左右曲线凹凸
正弦函数的性质与图像
数缺形时少直观,形缺数时难入微
五点作图
数形结合
借助单位圆分析性质
借助性质利用单位圆研究图像
根据图像进一步理解性质
例:不求值,比较 和 的大小.
单位圆
正弦函数的单调性
分析:求函数最值的本质是什么呢?
值域 函数的单调性
这类函数的最值问题如何处理呢?
换元法
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:函数 与 同时取得最值,
所以
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:令 ,则
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:根据二次函数闭区间上的单调性,可得
即 此时
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
解:根据二次函数闭区间上的单调性,
可得 即
或 ,此时
例:求下列函数的最大值和最小值,并求出取得最大值
和最小值时 的值.
例:用五点法作函数 的图像.
解:找关键的五个点,列表如下
例:用五点法作函数 的图像.
解:描点作图
位置关系?
向上平移
1个单位
小结
正弦函数
单位圆
抽象
函数图像
直观
数
形
核心任务:利用单位圆研究正弦函数的性质与图像
同角三角函数基本关系式
诱导公式
变量间的变化过程
变化趋势
作业
1.不求值,比较 和 的大小.
作业
2.求下列函数的最大值和最小值,并求出取得最大值和
最小值时 的值.
(1) (2) (3)
作业
3.用五点法作出下列函数在 上的图像,并说明它
们与 的图像的关系.
(1) (2)
感谢观看
