人教版六年级下册6.2.1图形的认识与测量(立体图形部分) 课件(37张ppt)
文档属性
| 名称 | 人教版六年级下册6.2.1图形的认识与测量(立体图形部分) 课件(37张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-15 08:38:08 | ||
图片预览







文档简介
(共37张PPT)
第六单元 整理与复习 2.图形与几何
人教版 数学 六年级下
立体图形的认识与测量
1.全面掌握小学阶段所学的立体图形的基本特征,能正确计算有关立体图形的表面积和体积,并能运用相关知识解 决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成
清晰的知识网络。
3.通过整理与复习,借助几何图形的直观性,增强我们的空间观
念和空间想象能力。
学习目标:
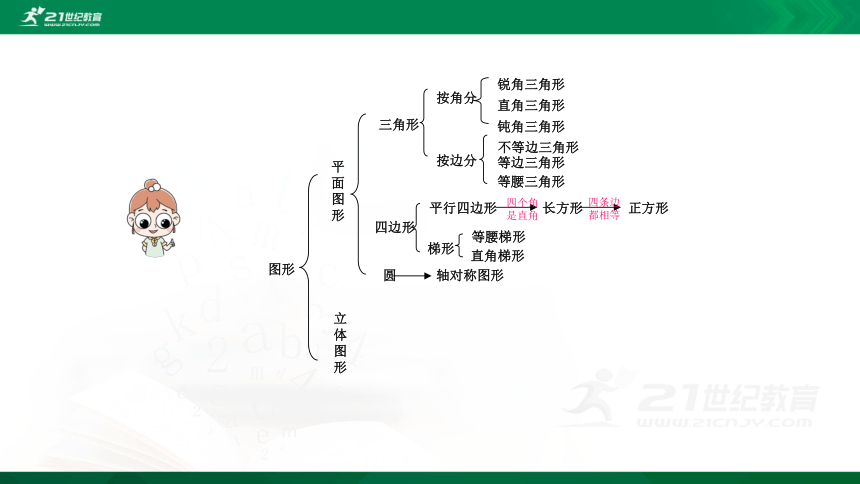
平
面
图
形
三角形
按角分
直角三角形
钝角三角形
按边分
不等边三角形
等边三角形
等腰三角形
四边形
平行四边形
四个角
是直角
长方形
四条边
都相等
正方形
梯形
等腰梯形
直角梯形
圆
轴对称图形
图形
锐角三角形
立体图形
在小学阶段都学过哪些立体图形呢?
每个面都是平面
都有一个面是曲面
长方体
正方体
圆柱
圆锥
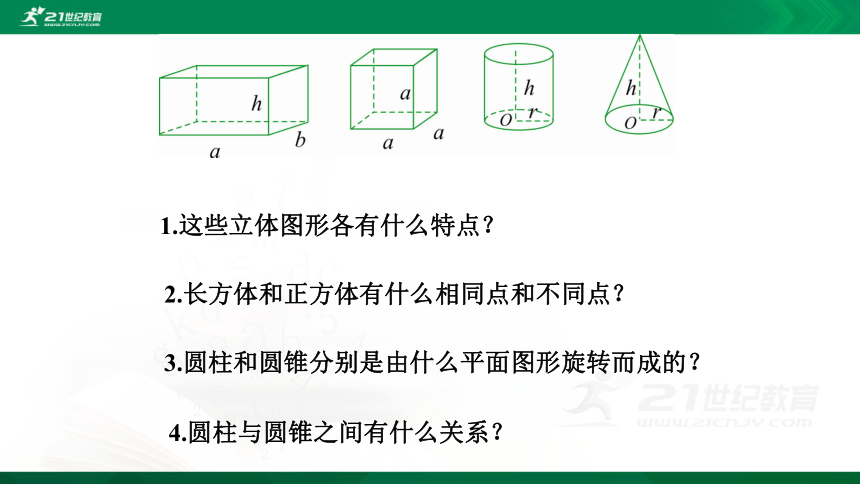
1.这些立体图形各有什么特点?
2.长方体和正方体有什么相同点和不同点?
3.圆柱和圆锥分别是由什么平面图形旋转而成的?
4.圆柱与圆锥之间有什么关系?
正方体是特殊的长方体
长方体、正方体、圆柱、圆锥的特征
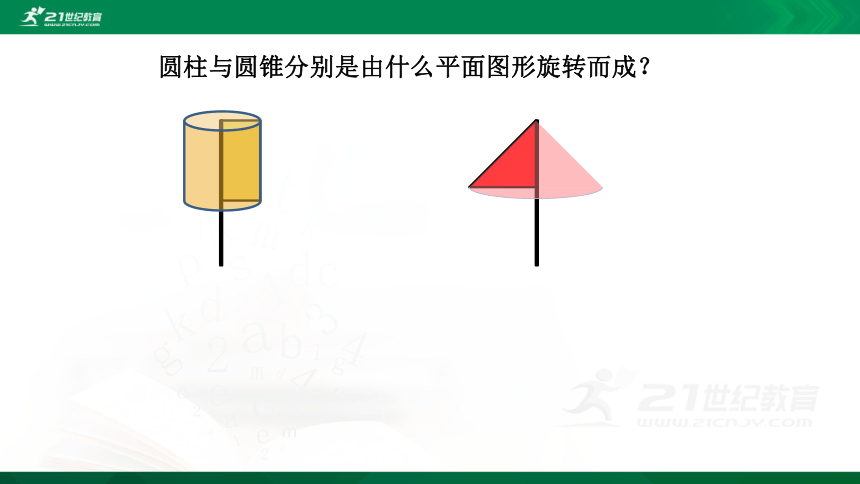
圆柱与圆锥分别是由什么平面图形旋转而成?
自主填写课本88页第5题的表格
表面积、体积
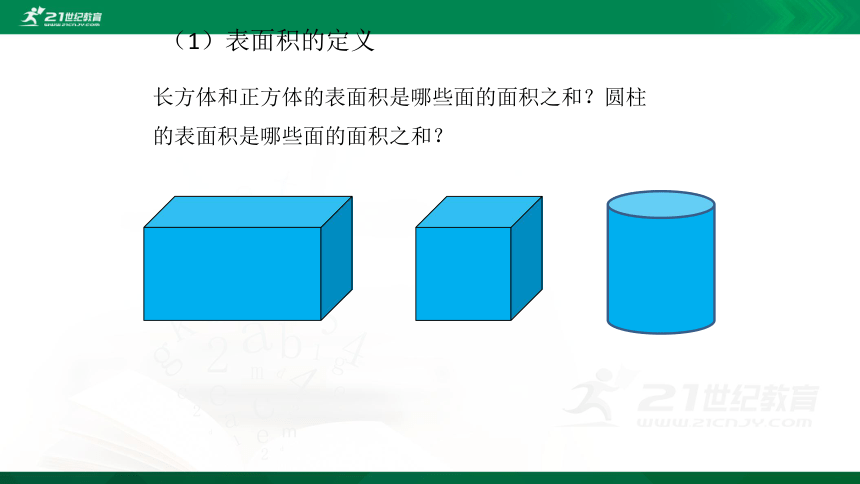
长方体和正方体的表面积是哪些面的面积之和?圆柱的表面积是哪些面的面积之和?
(1)表面积的定义
长方体和正方体的表面积是6个面的面积和。
(2)圆柱的表面积= +底面积×2
圆柱的侧面沿高展开是什么形状?侧面展开的长方形的长、宽与圆柱有什么关系?圆柱的侧面积怎样计算?
侧面积
展开的长方形的长等于圆柱的底面周长,宽等于圆柱的高。
圆柱的侧面积=底面周长×高。
底面
底面
底面的周长
底面
底面
高
底面的周长
高
什么样的圆柱沿高展开的侧面是正方形?
圆柱的底面周长和高相等时。
(3)归纳表面积的计算方法。
根据立体图形的表面积是围成立体图形所有面的面积,用字母表示出计算每个图形表面积的方法。
S长=2(ab+ah+bh)
S正=6a2
S圆柱=2πr2 +2πrh
实验观察
用体积为1cm3的小正方体摆成不同的长方体。
2. 体积的计算。
长:4
宽:2
高:2
小正方体的数量:16
长方体的体积:16
长:5
宽:2
高:2
小正方体的数量:20
长方体的体积:20
长:6
宽:2
高:1
小正方体的数量:12
长方体的体积:12
长:12
宽:1
高:1
小正方体的数量:12
长方体的体积:12
长 宽 高 小正方体的数量 长方体的体积
5 2 2 20 20
4 2 2 16 16
6 2 1 12 12
12 1 1 12 12
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
V=abh
V=a
长方体的体积
高
×
V = S h
=
=
底面积
×
高
圆柱体的体积
底面积
圆锥的体积是与它等底、等高的圆柱的体积的 。
V
圆锥
=
V
圆柱
=
3
1
3
1
Sh
三次正好装满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
3
1
V= Sh
3
1
这些图形有没有一个共同的体积计算公式呢?
V=abh
V=Sh
V=a
V= Sh
3
1
V=Sh
V=Sh
圆柱与圆锥之间有什么关系?
1.等底等高的圆柱和圆锥:圆柱的体积是圆锥体积的3倍,圆锥的体积是圆柱体积的 。
2.等底等体积的圆柱和圆锥:圆柱的高是圆锥的 ,圆锥的高是圆柱的3倍。
3.等高等体积的圆柱和圆锥:圆柱的底面积是圆锥底面积的 ,圆锥的底面积是圆柱底面积的3倍。
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
(3)至少需要多少平方米的玻璃?
(4)它的体积是多少?
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
1.小卖部要做一个长方体的无盖玻璃柜台,长是 ,宽是 ,高是 。
6m 60cm 1.5m
统一单位
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
长方体的棱长总和
60cm=0.6m
(6+0.6+1.5)×4
=8.1×2
=32.4(m)
答:至少需要32.4米的角铁。
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
底面积
6×0.6=3.6(m )
答:柜台的占地面积是3.6平方米。
1.小卖部要做一个长方体的 玻璃柜台,长是6m,宽是60cm,高是1.5m。
(3)至少需要多少平方米的玻璃?
5个面的面积
无盖
=3.6+(9+0.9)×2
=3.6+9.9×2
=3.6+19.8
=23.4(m )
答:至少需要23.4平方米的玻璃。
6×0.6+(6×1.5+0.6×1.5)×2
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(4)它的体积是多少?
体积=底面积×高
3.6×1.5=5.4(m )
答:它的体积是5.4立方米。
2.一个长方体容器,底面长2dm,宽1.5dm,将一个土豆完全浸没在水中,水面升高了0.2dm,这个土豆的体积是多少
2×1.5×0.2
=3×0.2
=0.6(dm3)
答:这个土豆的体积是0.6立方分米。
土豆的体积=上升的水的体积
0.2dm
3.把一个长方体木料长4m,如图截成三个一样大的小长方体,表面积增加60dm2,求原来长方体的体积是多少立方分米?
=15×40
=600(立方分米)
4m
4m=40dm
60÷4
×40
答:原来长方体的体积是600立方分米。
4.做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?
侧面积
18.84×4=75.36(dm )
答:至少需要铁皮75.36平方分米。
5.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米)
圆锥体积=正方体体积
10×10×10÷[ ×3.14×(20÷2) ]
=1000÷( ×314)
≈10(cm)
答:这个圆锥形铁块的高约是10厘米。
×3.14×(20÷2) x=10×10×10
×314x=1000
x=1000×
x≈10
答:这个圆锥的高约是10厘米。
解:设这个圆锥的高约是x厘米。
1.全面掌握小学阶段所学的立体图形的基本特征,能正确计算有关立体图形的表面积和体积,并能运用相关知识解
决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成
清晰的知识网络。
3.通过整理与复习,借助几何图形的直观性,增强我们的空间观
念和空间想象能力。
学习目标:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
第六单元 整理与复习 2.图形与几何
人教版 数学 六年级下
立体图形的认识与测量
1.全面掌握小学阶段所学的立体图形的基本特征,能正确计算有关立体图形的表面积和体积,并能运用相关知识解 决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成
清晰的知识网络。
3.通过整理与复习,借助几何图形的直观性,增强我们的空间观
念和空间想象能力。
学习目标:
平
面
图
形
三角形
按角分
直角三角形
钝角三角形
按边分
不等边三角形
等边三角形
等腰三角形
四边形
平行四边形
四个角
是直角
长方形
四条边
都相等
正方形
梯形
等腰梯形
直角梯形
圆
轴对称图形
图形
锐角三角形
立体图形
在小学阶段都学过哪些立体图形呢?
每个面都是平面
都有一个面是曲面
长方体
正方体
圆柱
圆锥
1.这些立体图形各有什么特点?
2.长方体和正方体有什么相同点和不同点?
3.圆柱和圆锥分别是由什么平面图形旋转而成的?
4.圆柱与圆锥之间有什么关系?
正方体是特殊的长方体
长方体、正方体、圆柱、圆锥的特征
圆柱与圆锥分别是由什么平面图形旋转而成?
自主填写课本88页第5题的表格
表面积、体积
长方体和正方体的表面积是哪些面的面积之和?圆柱的表面积是哪些面的面积之和?
(1)表面积的定义
长方体和正方体的表面积是6个面的面积和。
(2)圆柱的表面积= +底面积×2
圆柱的侧面沿高展开是什么形状?侧面展开的长方形的长、宽与圆柱有什么关系?圆柱的侧面积怎样计算?
侧面积
展开的长方形的长等于圆柱的底面周长,宽等于圆柱的高。
圆柱的侧面积=底面周长×高。
底面
底面
底面的周长
底面
底面
高
底面的周长
高
什么样的圆柱沿高展开的侧面是正方形?
圆柱的底面周长和高相等时。
(3)归纳表面积的计算方法。
根据立体图形的表面积是围成立体图形所有面的面积,用字母表示出计算每个图形表面积的方法。
S长=2(ab+ah+bh)
S正=6a2
S圆柱=2πr2 +2πrh
实验观察
用体积为1cm3的小正方体摆成不同的长方体。
2. 体积的计算。
长:4
宽:2
高:2
小正方体的数量:16
长方体的体积:16
长:5
宽:2
高:2
小正方体的数量:20
长方体的体积:20
长:6
宽:2
高:1
小正方体的数量:12
长方体的体积:12
长:12
宽:1
高:1
小正方体的数量:12
长方体的体积:12
长 宽 高 小正方体的数量 长方体的体积
5 2 2 20 20
4 2 2 16 16
6 2 1 12 12
12 1 1 12 12
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
V=abh
V=a
长方体的体积
高
×
V = S h
=
=
底面积
×
高
圆柱体的体积
底面积
圆锥的体积是与它等底、等高的圆柱的体积的 。
V
圆锥
=
V
圆柱
=
3
1
3
1
Sh
三次正好装满。
我把圆柱装满水,再往圆锥里倒。
正好倒了三次。
3
1
V= Sh
3
1
这些图形有没有一个共同的体积计算公式呢?
V=abh
V=Sh
V=a
V= Sh
3
1
V=Sh
V=Sh
圆柱与圆锥之间有什么关系?
1.等底等高的圆柱和圆锥:圆柱的体积是圆锥体积的3倍,圆锥的体积是圆柱体积的 。
2.等底等体积的圆柱和圆锥:圆柱的高是圆锥的 ,圆锥的高是圆柱的3倍。
3.等高等体积的圆柱和圆锥:圆柱的底面积是圆锥底面积的 ,圆锥的底面积是圆柱底面积的3倍。
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
(3)至少需要多少平方米的玻璃?
(4)它的体积是多少?
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
1.小卖部要做一个长方体的无盖玻璃柜台,长是 ,宽是 ,高是 。
6m 60cm 1.5m
统一单位
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(1)要在柜台各边都按上角铁,至少需要多少米的角铁?
长方体的棱长总和
60cm=0.6m
(6+0.6+1.5)×4
=8.1×2
=32.4(m)
答:至少需要32.4米的角铁。
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(2)柜台的占地面积有多大?
底面积
6×0.6=3.6(m )
答:柜台的占地面积是3.6平方米。
1.小卖部要做一个长方体的 玻璃柜台,长是6m,宽是60cm,高是1.5m。
(3)至少需要多少平方米的玻璃?
5个面的面积
无盖
=3.6+(9+0.9)×2
=3.6+9.9×2
=3.6+19.8
=23.4(m )
答:至少需要23.4平方米的玻璃。
6×0.6+(6×1.5+0.6×1.5)×2
1.小卖部要做一个长方体的无盖玻璃柜台,长是6m,宽是60cm,高是1.5m。
(4)它的体积是多少?
体积=底面积×高
3.6×1.5=5.4(m )
答:它的体积是5.4立方米。
2.一个长方体容器,底面长2dm,宽1.5dm,将一个土豆完全浸没在水中,水面升高了0.2dm,这个土豆的体积是多少
2×1.5×0.2
=3×0.2
=0.6(dm3)
答:这个土豆的体积是0.6立方分米。
土豆的体积=上升的水的体积
0.2dm
3.把一个长方体木料长4m,如图截成三个一样大的小长方体,表面积增加60dm2,求原来长方体的体积是多少立方分米?
=15×40
=600(立方分米)
4m
4m=40dm
60÷4
×40
答:原来长方体的体积是600立方分米。
4.做一节圆柱形的通风管,底面周长18.84分米,长4分米。至少需要铁皮多少平方分米?
侧面积
18.84×4=75.36(dm )
答:至少需要铁皮75.36平方分米。
5.把一块棱长10cm的正方体铁块熔铸成一个底面直径是20cm的圆锥形铁块。这个圆锥形铁块的高约是多少?(得数保留整厘米)
圆锥体积=正方体体积
10×10×10÷[ ×3.14×(20÷2) ]
=1000÷( ×314)
≈10(cm)
答:这个圆锥形铁块的高约是10厘米。
×3.14×(20÷2) x=10×10×10
×314x=1000
x=1000×
x≈10
答:这个圆锥的高约是10厘米。
解:设这个圆锥的高约是x厘米。
1.全面掌握小学阶段所学的立体图形的基本特征,能正确计算有关立体图形的表面积和体积,并能运用相关知识解
决生活中的实际问题。
2.通过分类、比较、辨析,进一步认识图形的区别与联系,形成
清晰的知识网络。
3.通过整理与复习,借助几何图形的直观性,增强我们的空间观
念和空间想象能力。
学习目标:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
