四年级下册数学课件-《整理与练习》多边形内角和 苏教版(共15张PPT)
文档属性
| 名称 | 四年级下册数学课件-《整理与练习》多边形内角和 苏教版(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-05-15 08:15:53 | ||
图片预览


文档简介
(共15张PPT)
多边形内角和
(第一课时)
1、多边形______两边组成的角叫做多边形的的内角。
2、各个内角____,各条边都_____的多边形叫做正多边形。
3、多边形的边数与它的内角个数________。
4、三角形的内角和等于__________。
5、长方形的内角和等于__________。
6、正方形的内角和等于__________。
相邻
相等
相等
180°
相等
360°
360°
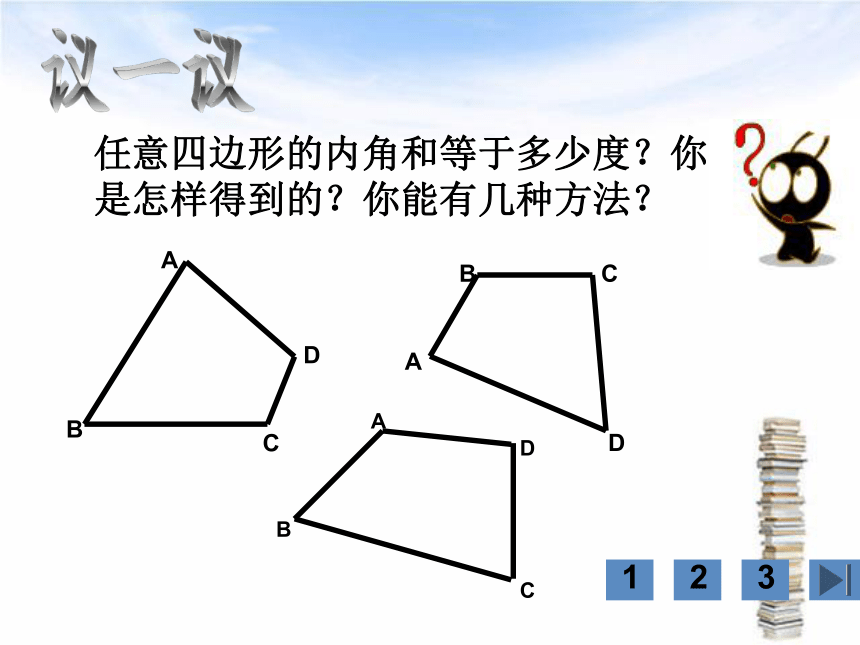
任意四边形的内角和等于多少度?你是怎样得到的?你能有几种方法?
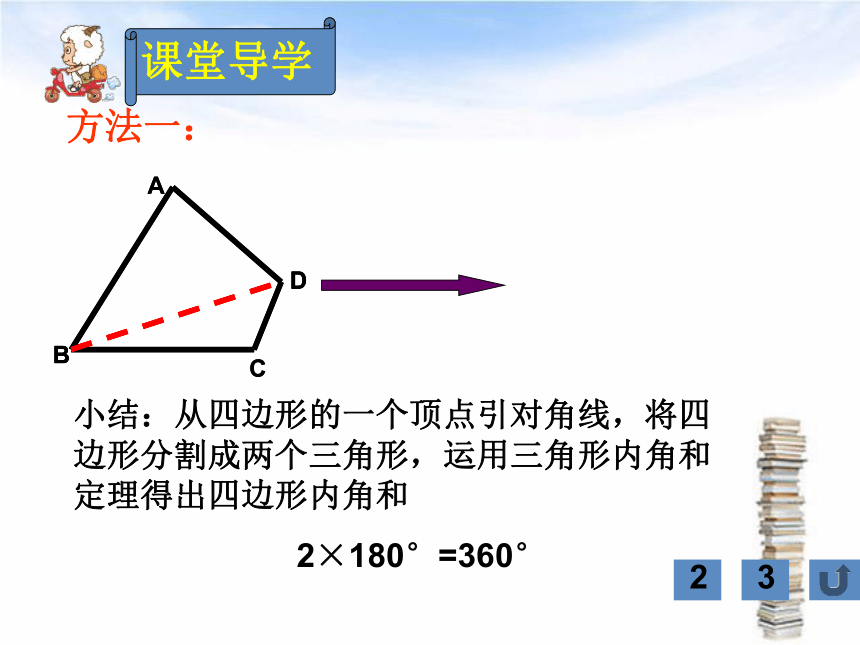
方法一:
小结:从四边形的一个顶点引对角线,将四边形分割成两个三角形,运用三角形内角和定理得出四边形内角和
2×180°=360°
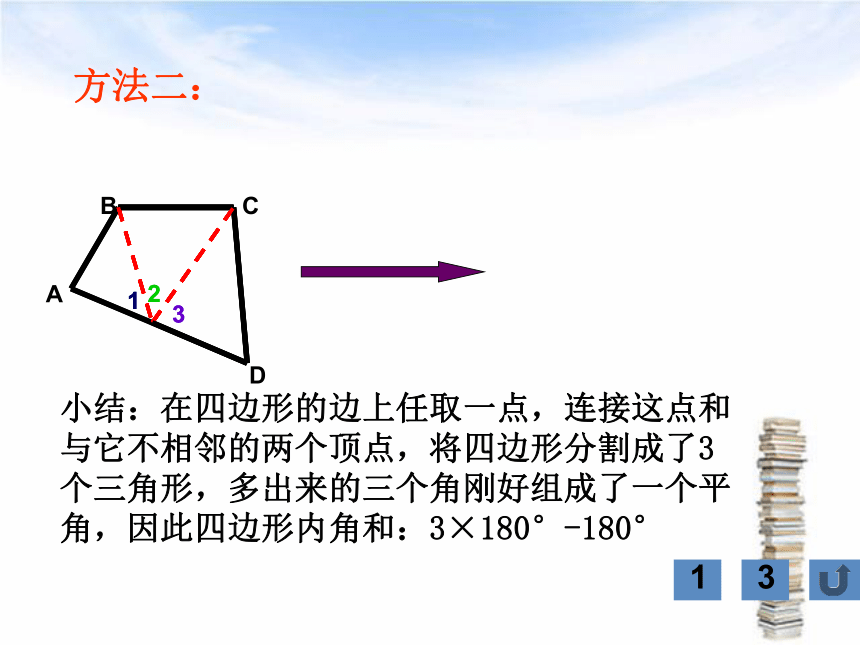
方法二:
小结:在四边形的边上任取一点,连接这点和与它不相邻的两个顶点,将四边形分割成了3个三角形,多出来的三个角刚好组成了一个平角,因此四边形内角和:3×180°-180°
1
2
3
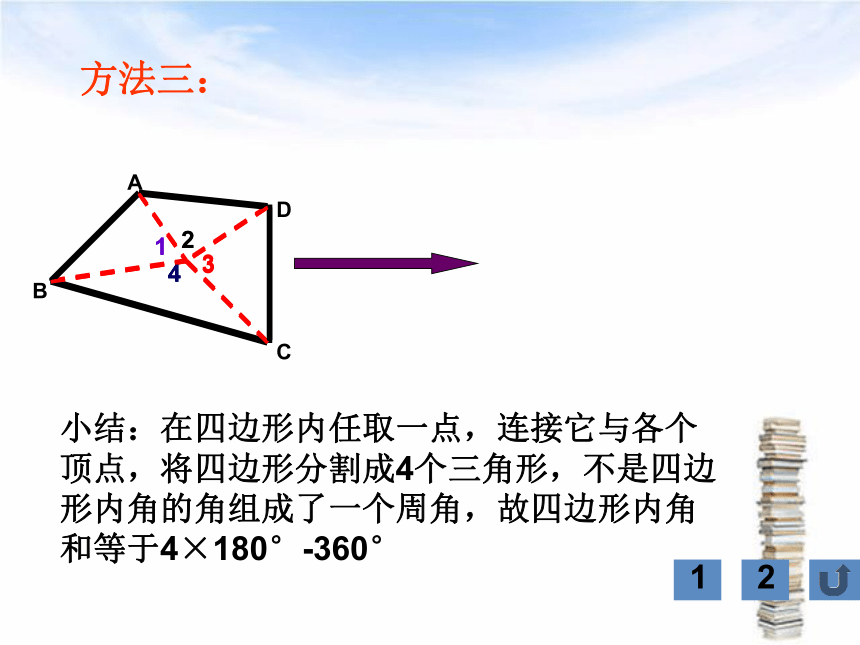
方法三:
小结:在四边形内任取一点,连接它与各个顶点,将四边形分割成4个三角形,不是四边形内角的角组成了一个周角,故四边形内角和等于4×180°-360°
1
2
3
4
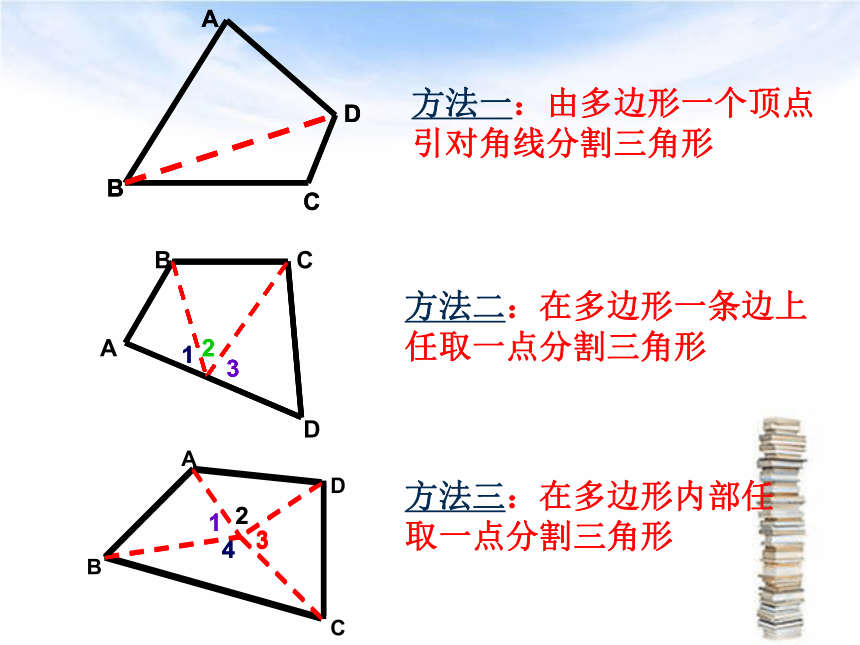
方法一:由多边形一个顶点引对角线分割三角形
方法二:在多边形一条边上任取一点分割三角形
方法三:在多边形内部任取一点分割三角形
1
2
3
4
n-2
…
…
180°
2×180°
3×180°
4×180°
(n-2)×180°
…
0
1
2
3
n-3
多边形 三角形 四边形 五边形 六边形 … n边形
从一个点出发引对角线的条数
分割成三角形的个数
内角和
3
3×180°-180°
4
4×180°-180°
5
5×180°-180°
n-1
(n-1)×180°
-180°
多边形 三角形 四边形 五边形 六边形 … n边形
分割成三角形的个数 …
内角和 180° …
4
5
6
n
4×180°-360°
5×180°-360°
6×180°-360°
n×180°
-360°
多边形 三角形 四边形 五边形 六边形 … n边形
分割成三角形的个数 …
内角和 180° …
n边形内角和公式
n边形的内角和等于(n-2)×180°
1、12边形的内角和等于_______
2、如果一个多边形的内角和等于1440°,那么这是___边形
1800°
十
已知边数求多边形内角和
已知多边形内角和求边数
(12-2)×180°=1800°
(n-2)×180°=1440°
n=10
例1 如果四边形的一组对角互补,那么另一组对角有什么关系?
解:如图,四边形ABCD中,
∠A+∠C=180°
∵∠A+∠B+∠C+∠D=(4-2)×180°=360°
∴ ∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°
结论:如果四边形的一组对角互补,那么另一组对角也互补。
1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____个三角形。
8
900°
108°
B
n-3
n-2
课堂小结
1、探索多边形内角和公式的方法
2、多边形的内角和公式(n-2)×180°
3、多边形内角和公式的简单应用
多边形内角和
(第一课时)
1、多边形______两边组成的角叫做多边形的的内角。
2、各个内角____,各条边都_____的多边形叫做正多边形。
3、多边形的边数与它的内角个数________。
4、三角形的内角和等于__________。
5、长方形的内角和等于__________。
6、正方形的内角和等于__________。
相邻
相等
相等
180°
相等
360°
360°
任意四边形的内角和等于多少度?你是怎样得到的?你能有几种方法?
方法一:
小结:从四边形的一个顶点引对角线,将四边形分割成两个三角形,运用三角形内角和定理得出四边形内角和
2×180°=360°
方法二:
小结:在四边形的边上任取一点,连接这点和与它不相邻的两个顶点,将四边形分割成了3个三角形,多出来的三个角刚好组成了一个平角,因此四边形内角和:3×180°-180°
1
2
3
方法三:
小结:在四边形内任取一点,连接它与各个顶点,将四边形分割成4个三角形,不是四边形内角的角组成了一个周角,故四边形内角和等于4×180°-360°
1
2
3
4
方法一:由多边形一个顶点引对角线分割三角形
方法二:在多边形一条边上任取一点分割三角形
方法三:在多边形内部任取一点分割三角形
1
2
3
4
n-2
…
…
180°
2×180°
3×180°
4×180°
(n-2)×180°
…
0
1
2
3
n-3
多边形 三角形 四边形 五边形 六边形 … n边形
从一个点出发引对角线的条数
分割成三角形的个数
内角和
3
3×180°-180°
4
4×180°-180°
5
5×180°-180°
n-1
(n-1)×180°
-180°
多边形 三角形 四边形 五边形 六边形 … n边形
分割成三角形的个数 …
内角和 180° …
4
5
6
n
4×180°-360°
5×180°-360°
6×180°-360°
n×180°
-360°
多边形 三角形 四边形 五边形 六边形 … n边形
分割成三角形的个数 …
内角和 180° …
n边形内角和公式
n边形的内角和等于(n-2)×180°
1、12边形的内角和等于_______
2、如果一个多边形的内角和等于1440°,那么这是___边形
1800°
十
已知边数求多边形内角和
已知多边形内角和求边数
(12-2)×180°=1800°
(n-2)×180°=1440°
n=10
例1 如果四边形的一组对角互补,那么另一组对角有什么关系?
解:如图,四边形ABCD中,
∠A+∠C=180°
∵∠A+∠B+∠C+∠D=(4-2)×180°=360°
∴ ∠B+∠D
=360°-(∠A+∠C)
=360°-180°
=180°
结论:如果四边形的一组对角互补,那么另一组对角也互补。
1、若一个多边形的内角和等于1080°,则这个多边形的边数是_______。
2、七边形的内角和等于_______。
3、正五边形的每个内角是________。
4、下列角度中,不能成为多边形的内角和的是( )
(A)540° (B)580° (C)1800° (D)900°
5、从n边形的一个顶点出发画对角线,最多可以画_____条,这些对角线把n边形分成_____个三角形。
8
900°
108°
B
n-3
n-2
课堂小结
1、探索多边形内角和公式的方法
2、多边形的内角和公式(n-2)×180°
3、多边形内角和公式的简单应用
